
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прогнозирование с помощью тренд – сезонных моделей
По временным рядам за лет в помесячном или поквартальном разрезе могут наблюдаться сезонные колебания. Сезонные колебания – это разновидность периодических колебаний. Для них характерны внутригодичные, повторяющиеся устойчиво из месяца в месяц (из квартала в квартал) изменения в уровнях, т.е. это регулярно повторяющиеся подъемы и снижение уровней ВР внутри года на протяжении ряда лет. Существует две модели сезонности: аддитивная и мультипликативная. В аддитивной модели сезонность выражается в виде абсолютной величины, которая добавляется или вычитается из среднего значения ряда, чтобы выделить показатель сезонности. В мультипликативной модели сезонность выражена как процент от среднего уровня, который должен быть учтен при прогнозировании путем умножения на него среднего значения ряда. Методика построения аддитивной и мультипликативной модели различается в зависимости от того, есть или нет тенденций в ряду динамики[16]. Если во ВР отсутствует тенденция, то уровень ряда рассматривается как функция сезонности и случайности (рис. 1.5):
где S – сезонная составляющая
Рис. 1.5. Стационарный временной ряд с сезонными колебаниями При аддитивной модели уровень такого ряда можно представить как:
Тогда: где Величина При мультипликативной модели уровень динамического ряда можно представить как произведение его составляющих: 
где отношение Чем больше коэффициент сезонности, тем больше амплитуда колебаний уровней ряда относительно его среднего уровня, тем существеннее влияние сезонности. Чем меньше влияние случайной составляющей, тем в большей мере рассматриваемая модель адекватно описывает исходный временной ряд. Прогнозирование динамического ряда с сезонными колебаниями при отсутствии в нем тенденции сводится к прогнозированию среднего уровня
Значительно распространена ситуация, когда динамический ряд имеет тенденцию. В этом случае уровень временного ряда рассматривается как функция тенденции (t), сезонности (S), и случайности
где S – сезонная составляющая;
Общая колеблемость уровней ВР раскладывается на 3 составляющие: где
Алгоритм построения тренд – сезонной аддитивной модели: 1. Проводят сглаживание временного ряда с помощью простой скользящей средней. Период скольжения должен быть равен 1 году (если период четный, то проводится центрирование скользящей средней); 2.Рассчитывают абсолютные показатели сезонности:
где
3.Рассчитывают средние показатели сезонности для одноименных кварталов (месяцев):
4.Если
5.Проводят десезоналирование временного ряда: из исходных уровней вычитаем скорректированную сезонную компоненту:
6.По десезоналированному временному ряду проводим аналитическое выравнивание. 7.рассчитываем тренд с учетом сезонности:
При мультипликативной модели уровень ВР можно представить в виде сомножителей:
где E – коэффициент влияния случайности Алгоритм построения тренд – сезонной мультипликативной модели: 1.Сглаживание ВР с помощью скользящей средней 2.Рассчитываем коэффициент сезонности
3.Определяем средние показатели сезонности для одноименных кварталов (месяцев):
4.Если при поквартальном наблюдении
5.Исключаем сезонность из уровней ряда:
6.Проводится аналитическое выравнивание десезоналированного ряда; 7.Рассчитываются уровни временного ряда, обусловленные влиянием тенденции и сезонности:
Аддитивная модель целесообразна, если размах сезонных колебаний изменяется слабо.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 928. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
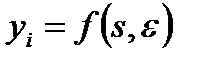 (6.1)
(6.1)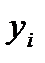 - фактические уровни ВР
- фактические уровни ВР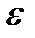 - случайная компонента
- случайная компонента
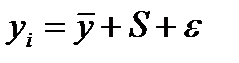 (6.2)
(6.2)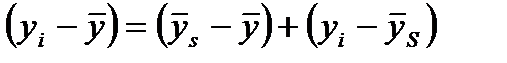
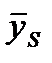 - средний уровень ряда соответствующего периода внутри года (месяца, квартала) за ряд лет.
- средний уровень ряда соответствующего периода внутри года (месяца, квартала) за ряд лет.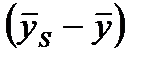 отражает влияние сезонности (сезонная составляющая S), а величина
отражает влияние сезонности (сезонная составляющая S), а величина 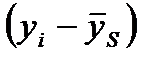 характеризует влияние случайной компоненты.
характеризует влияние случайной компоненты.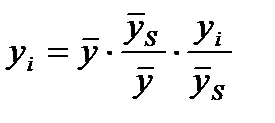 (6.3)
(6.3)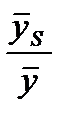 представляет собой коэффициент сезонности (
представляет собой коэффициент сезонности ( 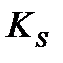 ), а
), а 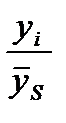 - отражает влияние случайного фактора.
- отражает влияние случайного фактора.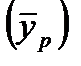 с последующей корректировкой его на сезонную компоненту:
с последующей корректировкой его на сезонную компоненту: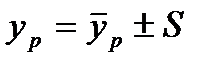 – аддитивная модель; (6.4)
– аддитивная модель; (6.4)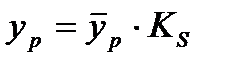 – мультипликативная модель. (6.5)
– мультипликативная модель. (6.5)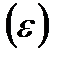 . Тогда аддитивная модель уровня динамического ряда примет вид:
. Тогда аддитивная модель уровня динамического ряда примет вид: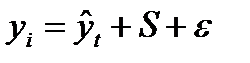 (6.6)
(6.6)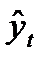 - теоретическое значение уровня ряда согласно тенденции;
- теоретическое значение уровня ряда согласно тенденции;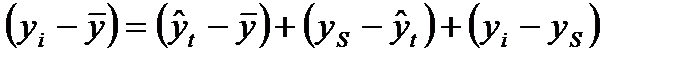 , (6.7)
, (6.7)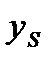 - тренд с учетом сезонности.
- тренд с учетом сезонности.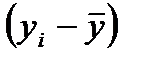 - общая вариация;
- общая вариация;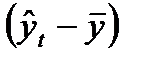 - влияние тенденции;
- влияние тенденции;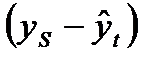 - влияние сезонности;
- влияние сезонности;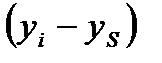 - влияние случайности.
- влияние случайности.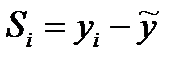 (6.8)
(6.8)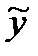 - выровненные скользящие средние;
- выровненные скользящие средние;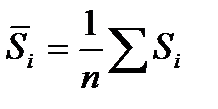 . (6.9)
. (6.9)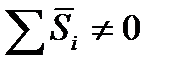 , проводится корректировка сезонной компоненты:
, проводится корректировка сезонной компоненты: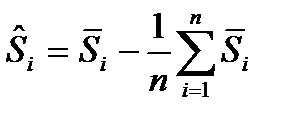 . (6.10)
. (6.10)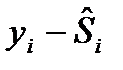 . (6.11)
. (6.11)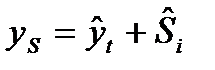 . (6.12)
. (6.12)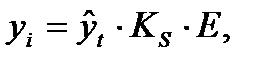 (6.13)
(6.13)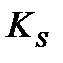 - коэффициент сезонности
- коэффициент сезонности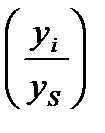 .
.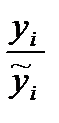 (6.14)
(6.14)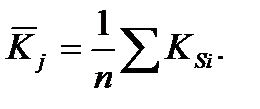
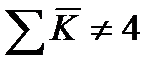 , а при помесячном
, а при помесячном 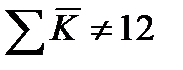 , то выполняется корректировка коэффициента сезонности:
, то выполняется корректировка коэффициента сезонности: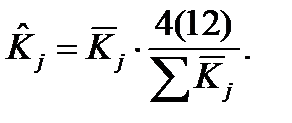 (6.15)
(6.15)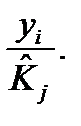 (6.16)
(6.16)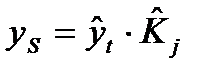 . (6.17)
. (6.17)