Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аппарат дисперсионного анализа1.Рассмотрим структуру эффектов однофакторной схемы (2.1.3) (эффект
Для двух других отклонений справедливы аналогичные соотношения: Рассмотрим сумму квадратов отклонений
Суммируя почленно, будем иметь
Суммируя оставшиеся слагаемые, получаем
откуда, на основании (2.2.1), (2.2.2), получаем тождественный ноль. Так, приходим к тождеству Полученное соотношение (2.2.3) носит название основное уравнение дисперсионного анализа. Каждая из компонент суммы квадратов имеет число степеней свободы, как было показано в п.1.4, равное количеству независимых нормальных СВ (совокупности, из которых получены групповые выборки, априорно полагаются нормальными). Для определения числа степеней свободы существует простое мнемоническое правило: число степеней свободы = количество слагаемых в связывающей их сумме – количество уравнений. Для суммы квадратов эффекта 
Таким образом, численной мерой изменчивости отклика служит сумма квадратов отклонений Q, которая, как гласит основное уравнение дисперсионного анализа, может быть представлена в виде суммы парциальных сумм квадратов QA+Qe – компонент, характеризующих вклад в полную изменчивость отклика каждого из источников изменчивости. Однако непосредственное сравнение величин QA и Qe не позволяет сделать обоснованный вывод о том, какой из источников является более значимым (весомым). Поскольку у каждой компоненты свое число степеней свободы, то представляется естественным сравнивать между собой средние квадраты отклонений (на одну степень свободы): При этом вполне очевидно, что методика сравнения (оценки значимости эффекта фактора) должна строиться исходя из вероятностного содержания основных исходных допущений (о нормальности и взаимной независимости всех индивидуальных значений). Единственно возможным в данной ситуации представляется использование аппарата дисперсионного анализа, конечно, если сами исходные данные не находятся в явном противоречии с теми самыми исходными допущениями. 2. В предыдущем пункте путем простых рассуждений было установлено, что численной мерой, характеризующей каждый из источников изменчивости, является средний квадрат отклонения и обоснована применимость дисперсионного анализа. Вероятностное содержание исходных допущений при более детальном рассмотрении заключается в наличии всего двух альтернативных гипотез: · · По существу, все проблемы дисперсионного анализа, так или иначе, вращаются вокруг этих двух альтернатив. При этом к формулировке гипотезы 1) очевидно, что она (вместе с 2) поскольку Для уяснения «механизма» использования дисперсионного анализа найдем МО средних квадратов (2.2.4) для каждой из гипотез. Для
Используя свойство МО (п.1.1), последнее соотношение преобразуем к виду
Далее, используя соотношение для дисперсии, получим
Данное тождество было получено применительно к условиям Теперь найдем МО
Применяя аналогичную последовательность преобразований и учитывая, что
Таким образом, можно считать доказанной теорему Фишера, которую в контексте предыдущего изложения можно сформулировать так: При справедливости гипотезы Отсюда следует, что отношение средних квадратов есть рассмотренное в п.1.2 дисперсионное отношение Фишера:
Здесь следует сделать следующее замечание. Закону Фишера будет (в рамках
Однако практический интерес представляет лишь ситуация Для МО
В последнем выражении общее генеральное среднее В результате после элементарных преобразований окончательно получаем
где Несмещенная оценка этой компоненты дисперсии согласно (2.2.8) будет иметь вид
Таким образом, доказана теорема Эрвина о выделении эффекта фактора, и алгоритм дисперсионного анализа в простейшем однофакторном случае заключается в следующем: 1) вычисляются средние квадраты 2) вычисляется их отношение
3) если 3.Изложенные в предыдущем пункте результаты и методика легко обобщаются на случай двух и большего числа факторов. Наибольшую сложность и, соответственно, интерес представляет переход от однофакторной к двухфакторной схеме. Пусть факторы
Точками условимся обозначать индексы, исчезающие при повышении порядка усреднения. Принимая за начало отсчета общий средний результат
соотношения для эффектов получим в виде:
где Соотношение (2.2.11), являющееся очевидным тождеством, содержит уже 4 источника изменчивости. Принципиальным отличием двухфакторной схемы является наличие третьего слагаемого в (2.2.11) – так называемого взаимодействия факторов. Первые два называются главными эффектами факторов. Последнее, как и в предыдущем случае, ошибка эксперимента. Для лучшего уяснения смысла вновь возникшего феномена – (А×В)-взаимодействия – следует сделать небольшое отступление. Факторы Наглядно это можно легко себе представить на простом модельном примере. Пусть Изобразим графически зависимость
а б в Рис. 2.2.1. Схема двухфакторного взаимодействия
На рис. 2.2.1а,б При большем числе факторов геометрическую интерпретацию дать уже невозможно, но «механизм» взаимодействия будет тем же самым. Возвращаясь к схеме дисперсионного анализа, возведем обе части (2.2.11) в квадрат и просуммируем по всем
где частичные суммы соответственно равны:
Вывод (2.2.12) не содержит ничего принципиально отличающегося от (2.2.3): перекрестные произведения при суммировании обнуляются, а это, в свою очередь, напрямую вытекает из соотношений, аналогичных (2.2.1), (2.2.2). Число степеней свободы каждой частичной суммы определяется, как и в однофакторной схеме: количество слагаемых, входящих в сумму, – количество уравнений – связей. Для
Для остальных компонент соотношение очевидно, и получаем
Далее, как и в однофакторной схеме, находим средние квадраты отклонений:
Значимость каждого из трех источников контролируемой изменчивости оценивается по величине дисперсионного отно- шения 4. При увеличении количества факторов соотношения, аналогичные (2.2.11)
Частичные суммы квадратов и числа степеней свободы составят соответственно:
Значимость каждого из 7 источников контролируемой изменчивости оценивается точно так же по величине дисперсионного отношения 5. Одной из важнейших задач дисперсионного анализа является ранжирование значимых источников изменчивости. По завершении процедуры собственно дисперсионного анализа значимыми признаются только те эффекты и взаимодействия, у которых средние квадраты значительно превышают средний квадрат случайной ошибки (
где Именно на основании полученного по (2.2.19), (2.2.20) числового ряда и делаются выводы об объекте исследования в знакомой всем формулировке примерно такого содержания: «… продолжительность жизни на 30% определяется чистотой воздушной среды, на 20% - качеством потребляемой питьевой воды и т.д. …». Планы со смешиванием эффектов и Дробные многофакторные планы 1.В п. 2.2 было определено понятие межфакторного взаимо-действия , заключающегося в том, что изменчивость отклика при варьировании одного фактора зависит от уровня другого фактора (или других факторов). При явно значимом двухфакторном взаимо-действии наблюдается инверсия эффекта одного фактора при смене уровней второго фактора. При этом аппарат многофакторного дис-персионного анализа (п. 2.2) позволяет оценивать значимость как главных эффектов, так и взаимодействий любого порядка, посредством единообразной вычислительной процедуры. Однако в ряде случаев возникают ситуации, когда взаимодействие, даже если оно является явно значимым, не может быть сколько-нибудь вразумительным образом интерпретировано. Одним из наиболее характерных примеров являются так называемые эксперименты с группировкой, или иерархические. Такая ситуация возникает, когда уровни одного фактора локализованы (сгруппированы) внутри уровней другого фактора (или внутри пересечения уровней нескольких факторов). В этом случае уровни вложенного фактора, очевидно, не пересекаются с уровнями внешних и, стало быть, ни о каком взаимодействии говорить не имеет смысла. В двухфакторном эксперименте с группировкой следует модифицировать схему дисперсионного анализа таким образом, чтобы эффект взаимодействия смешивался с главным эффектом вложенного фактора. Полученную смесь, т.е. сумму эффектов, вполне естественно можно интерпретировать как уточненный эффект вложенного фактора. В качестве примера рассмотрим эксперимент, целью которого является оценка однородности продукции нескольких многопозиционных станков. Пусть 5 станков, на которых изготавливаются стеклянные держатели катода электронных ламп имеют по 4 позиции (головки), на которых формуются держатели. В результате образуется план-матрица двухфакторного эксперимента типа 5х4. Приняв численность каждой из 20 элементарных ячеек эксперимента n=4 индивидуальных значений деформации держателя, получим N=80 индивидуальных значений. Результаты полностью рандомизованного эксперимента приведены в табл. 2.3.1.
Таблица 2.3.1. Исходные данные эксперимента
Окончание табл. 2.3.1
Структура эффектов такого эксперимента будет иметь вид
Слагаемые в правой части (2.3.1) интерпретируются как эффект станка, эффект головки внутри станка и случайная ошибка эксперимента соответственно. Возводя обе части (2.3.1) в квадрат и суммируя по всем j,i,n, получим сумму квадратов, структурированную по источникам изменчивости: где
Легко заметить, что смешивание эффектов в данном случае сводится к суммированию соответствующих величин двухфакторного эксперимента с пересекающимися уровнями:
где
Таблица 2.3.2. Результаты дисперсионного анализа
Окончание табл. 2.3.2
Следует отметить еще одно отличие в рассмотренной схеме дисперсионного анализа по сравнению с «обычным» двухфакторным экспериментом. Значимость эффекта вложенного фактора оценивается по дисперсионному отношению со средним квадратом ошибки ( По результатам табл. 2.3.2 можно сделать вывод, что следует обратить внимание на различие между головками одного станка. Дисперсионный анализ данных табл. 2.3.1 по схеме с выделенным эффектом взаимодействия привел бы и абсурдному выводу об однородности как головок, так и станков, но при наличии значимого взаимодействия между ними (рекомендуется убедиться в этом, проделав вычисления самостоятельно). Сходная с рассмотренной ситуация возникает при интерпретации исходных данных контрольной процедуры статистической оценки воспроизводимости и сходимости измерительного процесса, прописанной в разделе MSA ISO. Выборка операторов из состава оперативного персонала проводит серию контрольных измерений партии стандартных образцов. В образующемся двухфакторном эксперименте изменчивость между операторами (воспроизводимость) следует вычислять по схеме смешения главного эффекта оператора и взаимодействия оператор × образец. В противном случае затруднительно интерпретировать результат индивидуального оператора, усредненный по всем образцам и попыткам. 2.В рассмотренных ситуациях необходимость смешивания эффектов и схема смешивания определяются, исходя из интерпретации самих исходных данных. Гораздо более интересными как в теоретическом, так и в практическом аспекте являются ситуации, когда смешивание является неизбежным следствием неполноты (усеченности) исходных данных, т.е. когда исходные данные представляют собой не все, а только часть точек (комбинаций уровней) факторного пространства. Усечение факторного пространства возможно двумя способами : – разбиением на блоки (блочные многофакторные планы); – насыщением дополнительными факторами, что фактически является построением одного блока из пространства большей размерностью (дробные многофакторные планы). Следуя хронологии развития и сложившейся традиции изложения в учебных курсах по планированию эксперимента, блочные и дробные планы излагаются раздельно и именно в такой последовательности. Однако, поскольку имеется ввиду, по существу, один и тот же феномен, представляется целесообразным рассмотреть эти два типа планов совместно и с единых позиций. Попутно следует заметить, что именно на примере этих планов становится очевидным, насколько существенным является сам термин планирование и насколько велика его (планирования) практически значимость. В качестве иллюстрации рассмотрим следующий пример. Предположим, химик желает определить однородность раствора в лабораторном сосуде по глубине и расстоянию от стенки. Для этого он решает взять пробы в 4 точках сосуда в соответствии со схемой рис. 2.3.1.
Рис. 2.3.1. Расположение точек забора проб
Полученный план имеет тип 22, А - расстояние от оси, В - глубина погружения. Однако у лаборанта всего две руки, и без специального приспособления он может брать только две пробы. Для реализации всего эксперимента потребуется два погружения, между которыми пройдет некоторое время, и концентрации в растворе, вообще говоря, могут измениться. Таким образом, весь эксперимент разделяется на два блока, которые являются «паразитным» источником изменчивости и выступают как неизбежное зло. Вопрос заключается в том, как путем надлежащего планирования минимизировать ущерб. Из
Таблица 2.3.3. Варианты блоков
Легко видеть, что в I варианте главный эффект А и А×В взаимодействие смешиваются с эффектом блока. В варианте II с эффектом блока смешиваются В и А×В. И только в III варианте оба главных эффекта отделяются от эффекта блока. Смешанным остается только АхВ взаимодействие. 3.Что бы оценить, в чем заключается сходство и различие между блочными и дробными планами, используем ту же самую модель эксперимента. Дополним эксперимент третьим фактором - временем С , который будет варьировать также на двух уровнях: t1~1, t2~c. В результате образуется эксперимент типа 23 . Для удобства вычислительной процедуры проведем кодирование уровней факторов, положив нижний -1, верхний +1, и впишем все 8 комбинаций условий эксперимента в табл. 2.3.4.
Таблица 2.3.4. Комбинации условий испытаний
Желая уложиться в 4 опыта, исследователь должен смириться с неизбежной потерей части информации. Априорно наименее цен-ным является старшее взаимодействие АхВхС. Группируя опыты (строки табл. 2.3.4) так, чтобы значение в столбце АВС имели одинаковый знак, получим 2 блока (2 полуреплики) эксперимента 23. При этом тройное взаимодействие станет «невидимым», кроме того, произойдет смешивание главных эффектов с парными взаимодействиями: А ~ ±ВС, В ~ ±АС, С ~ ±АВ. Таким образом, дробный многофакторный план представляет собой один из блоков полного плана. Знак в схеме смешивания определяется выбором блока, который, в свою очередь, выбирается случайно (блоки рандомизуются). Если блок рассматривать как источник изменчивости, равноправный с факторами (число уровней этого дополнительного фактора очевидно равно количеству блоков), то принципиальное различие между блочными и дробными планами и вовсе исчезает. Алгоритм разбиения на блоки, так называемый метод определяющих контрастов, строится с помощью элементов теории групп. Кемпторн предложил рассматривать линейную форму:
где λi – показатель степени i-го фактора в определяющем контрасте, Xi - уровень i-го фактора в данной комбинации условий. Сам определяющий контраст записывается как взаимодействие (или главный эффект), смешиваемое с эффектом блока. В рассмотренном примере контраст – парное взаимодействие АхВ имеет линейную форму L=X1+X2. Все комбинации условий (уровней факторов) разбиваются на классы эквивалентности, как группа L mod m, где m – число уровней факторов (должно быть одинаковым). Блоки формируются из комбинаций, принадлежащих одному классу эквивалентности. При этом блок, содержащий комбинацию (1) (все факторы на нижних уровнях), называется основным. Для рассмотренного примера будем иметь: (1): L = 1∙0 + 1∙0 = 0 ≡ 0 mod 2, a : L = 1∙1 + 1∙0 = 1 ≡ 1 mod 2, b : L = 1∙0 + 1∙1 = 1 ≡ 1 mod 2, ab : L = 1∙1 + 1∙1 = 2 ≡ 0 mod 2. В результате получаем III вариант разбиения на блоки в соответствии с табл. 2.3.3. В экспериментах типа 2n при n>2 количество возможных вариантов разбиения будет существенно большим. Для эксперимента 23 при возможности реализации лишь четырех комбинаций условий и смешивании с эффектом блока старшего взаимодействия А×В×С, будем иметь: L = X1 + X2 + X3, (1): L≡0 mod 2, a : L≡1 mod 2, b : L≡1 mod 2, c : L≡1 mod 2, ab : L=2≡0 mod 2, ac : L=2≡0 mod 2, bc : L=2≡0 mod 2, abc : L=3≡1 mod 2. Группируя комбинации с равными значениями L mod 2, получаем 2 блока:
Блок I (L=0) Блок II (L=1)
В таком блочном плане с эффектом блока смешивается старшее взаимодействие АхВхС. Все главные эффекты и парные взаимодействия остаются выделенными. В общем случае, при разбиении эксперимента типа 2n на m блоков (m должно быть кратно 2) с эффек-том блока смешиваются m-1 эффектов или взаимодействий. Какие именно эффекты будут смешаны с эффектом блока и составляет, собственно, предмет планирования эксперимента. В качестве примера рассмотрим эксперимент 24 в ситуации, когда в один блок мо- гут входить только 4 комбинации условий, что соответствует 4- блочному плану эксперимента 24. В качестве двух альтернатив рассмотрим две схемы смешения: а) АхВ, СхD, АхВхСхD; б) АхВхС, ВхСхD, АхD. Легко заметить, что каждая тройка эффектов представляет собой группу относительно умножения mod 2 (при перемножении любых двух эффектов из тройки получится третий). Для каждой из альтернатив получаем два определяющих контраста:
а) L1 = X1 + X2, L2 = X3 + X4; б) L1 = X1 + X2 + X3, L2 = X2 + X3 + X4 (или X1 + X4). (2.3.6)
Блоки формируются по принципу соответствия L1 (mod 2) и L2 (mod 2). Значения контрастов в 16 точках полного плана приведены в табл. 2.3.5 а, б.
Таблица 2.3.5а
Таблица 2.3.5 б
Группируя комбинации условий по классам эквивалентности пары (L1, L2), получаем два варианта разбиения на блоки, как показано в табл. 2.3.6 а, б. Таблица 2.3.6 а
Таблица 2.3.6 б
4.Планы типа wn, где w>2 простое число, разбиваются на кратное w число блоков. Блоки формируются в соответствии со структурой группы (mod w). Например, если эксперимент типа 32, содержащий 9 комбинаций условий, разбивается на 3 блока и с эффектом блока смешивается взаимодействие АхВ2, то определяющий контраст имеет вид L = X1 + 2X2. (2.3.7) Значения контраста в 9 вершинах факторного пространства приведены в табл. 2.3.7. Таблица 2.3.7
По классам эквивалентности L (mod 3) получаем 3 блока эксперимента 32, как показано в табл. 2.3.8. Таблица 2.3.8
В таком блочном плане остаются выделенными оба главных эффекта и парное взаимодействие. Причем, взаимодействие, как и главные эффекты, имеет число степеней свободы (в полностью рандомизованном эксперименте 32 АхВ – взаимодействие имеет (w-1)2 степеней свободы). Недостающие (w-1)(w-2) степеней свободы переходят в эффект блока, и в результате 8 степеней свободы эксперимента 32 разделяются, как показано в табл. 2.3.9.
Таблица 2.3.9
5.Как уже было отмечено, дробный план, назначением которого является минимизация трудоемкости (ценой частичной потери информации), представляет собой один из блоков полного многофакторного плана. Соответственно, все вышесказанное о смешивании эффектов и об алгоритме расщепления полного плана на блоке остается справедливым и для дробных планов. Единственным отличием , имеющим скорее терминологический характер, является то, что в роли эффекта блока выступает один из эффектов или взаимодействий. Некоторые авторы трактуют построение дробных планов как насыщение плана меньшей размерности дополнительными факторами. Пример насыщения эксперимента 22 третьим фактором (до полуреплики 23) был рассмотрен в плане параграфа. Следует заметить , что данный пример носит чисто иллюстративный характер, поскольку дробные реплики эксперимента типа w3 по большому счету не имеют практического значения (снижение трудоемкости незначительно, а потеря информации непомерно высока). Польза от дробных планов становится очевидной лишь при большом числе факторов (n≥4). В качестве примера рассмотрим план типа 27, содержащий 128 комбинаций условий. Переходя к полуреплике из 64 комбинаций ценой потери старшего взаимодействия, получим определяющий контраст в виде L=ABCDEFG. (2.3.8) Схему смешивания определяем поочередно, умножая (2.3.8) на символы главных эффектов и взаимодействий младших порядков, учитывая, что четные степени исчезают 0 ( mod 2) : A ∙ L = BCDEFG; AB ∙ L = CDEFG и т.д. Таким образом, в полуреплике 27 наряду с исчезновением (смешиванием с эффектом блока) старшего взаимодействия, взаимодействия 6-го порядка смешиваются с главными эффектами (не участвующими во взаимодействии), взаимодействия 5-го порядка смешиваются с непересекающимися парными и, наконец, взаимодействия 4-го порядка смешиваются с непересекающимися тройными. При однократной реализации полуреплики 27 с выбранной схемой смешения взаимодействия 3-го и 4-го порядков можно использовать в качестве оценки ошибки, тогда, пренебрегая взаимодействиями более старшего порядка, можно оценивать все главные эффекты и парные взаимодействия. При построении ¼ реплики эксперимента 27 оказывается предпочтительнее исключить 2 взаимодействия 5-го порядка (а стало быть, и их произведение). В результате все главные эффекты сме-шиваются с взаимодействиями 3-го и более высокого порядков, но при этом из 21 парных взаимодействий 6 оказываются смешанными между собой. Исключив взаимодействия AxBxCxDxE и CxDxExFxG, получим определяющий контраст следующего вида: L = ABCDE = CDEFG = ABFG. (2.3.9) Схема смешения, соответствующая контрасту (2.3.9), приведена в табл. 2.3.10. Таблица 2.3.10. Схема смешения ¼ реплики эксперимента 27
В некоторых случаях насыщение планов дополнительными факторами и переход к дробным репликам оказывается предпочтительнее полных планов с меньшим числом факторов. Планы эксперимента для исследования Поверхности отклика
1. Под понятием поверхность отклика подразумевается геометрическая интерпретация точной регрессионной зависимости, как функции многих переменных – факторов эксперимента:
Целью эксперимента в данной ситуации является не столько установление собственно формы зависимости (2.4.1), а то, чтобы с минимальными временными и иными затратами по возможности определить положение экстремальной точки этой поверхности в реализуемом диапазоне варьирования факторов. Если отклик интерпретируется как выход некоего продукта, то очевидно целью является точка максимума. Если же отклик представляет собой издержки, то, соответственно, целью будет точка минимума. Задачи подобного типа известны в численных методах оптимизации, когда требуется найти экстремум некоторой детерминированной функции многих переменных, имеющей сложный вид. Общей проблемой здесь является то, что для гарантированной результативности какой-либо из простейших схем последовательного поиска необходимым условием является гладкость и унимодальность (существование не более чем одного экстремума) в исследуемой области пространства. Из сказанного ясно, что реальная практическая польза от экспериментов данного типа определяется тем, насколько соответствуют действительности эти априорные гипотезы. Простейший вариант схемы эксперимента для поиска экстремума включает 2 этапа. Сначала по минимальному числу экспериментальных точек N=2k, где k- число факторов, строится линейная аппроксимация регрессии. На полученной плоскости определяется направление градиентной линии, точки (ядро плана) смещаются в нужном направлении (по градиенту в сторону максимума и в противоположном – в сторону минимума), и эксперимент повторяется при новых значениях уровней факторов. Критерием остановки такой итерационной процедуры служит либо инверсия градиента на очередном шаге (такая ситуация характерна при большом шаге смещения), либо стабилизация направления градиента значений отклика. Вторая ситуация характерна для малой величины шага смещения по факторному пространству. В геометрической интерпретации это означает, что аппроксимирующая плоскость заняла положение, близкое к горизонтальному (достигла почти стационарной области). В рассмотренной процедуре, вообще говоря, существует возможность выхода за границы реализуемого диапазона варьирования факторов без попадания в почти стационарную область. Это означает, что либо экстремума не существует, либо траектория движения прошла мимо области экстремума. Вторая фаза активного эксперимента заключается в более детальном обследовании области предполагаемого экстремума. Для этого к ядру плана добавляется еще некоторое количество точек (рассмотрим схему N=2k+2k+1). Для оценки случайной ошибки эксперимент по рандомизованной процедуре дублируется во всех или нескольких точках нового плана. Затем по средним значениям методом наименьших квадратов регрессия отклика аппроксимируется поверхностью 2-го порядка. Если полученная аппроксимация имеет удовлетворительную адекватность, то в качестве искомого экстремума отклика принимается точка экстремума аппроксимирующей поверхности 2-го порядка. При этом следует сделать оговорку, что достоинства поверхностей 2-го порядка исчерпываются их полной классификацией (4 типа), минимальным объемом вычислений по методу наименьших квадратов и, в целом, тем, что они представляют собой простейшую степенную функцию, имеющую экстремум. О «физическом» смысле такой аппроксимации в общем случае сказать ничего нельзя. 2.Детали алгоритма и, в частности, ортогональные преобразования и вычислительную процедуру метода наименьших квадратов рассмотрим на модельном примере. В качестве модельного двухфакторного объекта возьмем биквадратный параболоид
в области Минимум (2.4.2) очевидно находится в точке (0,0), но для наглядного представления о процедуре последовательного линейного градиентного спуска условимся, что наш виртуальный эксперимент будет заключаться в вычислении функции (2.4.2) в выбранных экспериментальных точках плоскости x1ox2. При этом «притворимся», что сама поверхность, задаваемая (2.4.2), нам не видна. В принципе можно добиться большого сходства с натурным экспериментом, добавив к (2.4.2) случайное слагаемое Z с нулевым средним. Тогда при повторных вычислениях в одной точке функция будет изме-няться, и вместо поверхности будем наблюдать поле рассеяния в 3-мерном пространстве, регрессией которого будет поверхность (2.4.2). Пусть на первом шаге факторы варьируются в соответствии с табл. 2.4.1. Таблица 2.4.1. План-матрица эксперимента на первом шаге
Линейную аппроксимацию регрессии ищем в виде |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 420. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
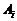 и ошибку
и ошибку 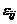 ). Для эффекта
). Для эффекта  . (2.2.1)
. (2.2.1)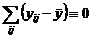 ,
, 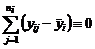 ,
, 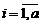 . (2.2.2)
. (2.2.2)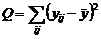 . Произведя то же самое действие с правой частью (2.1.3), получим
. Произведя то же самое действие с правой частью (2.1.3), получим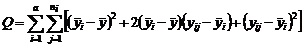 .
.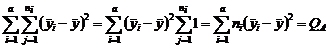 ;
;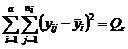 .
. ,
,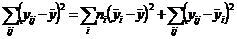 , или, в принятых обозначениях:
, или, в принятых обозначениях: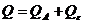 . (2.2.3)
. (2.2.3)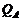 имеем
имеем 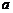 слагаемых и одно уравнение (2.2.1). Следовательно, число степеней свободы составит
слагаемых и одно уравнение (2.2.1). Следовательно, число степеней свободы составит 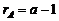 . У суммы квадратов случайной ошибки
. У суммы квадратов случайной ошибки 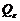 на
на 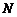 слагаемых приходится
слагаемых приходится 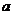 уравнений (2.2.2) (по количеству групп). Число ее степеней ошибки
уравнений (2.2.2) (по количеству групп). Число ее степеней ошибки 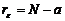 . И, наконец, для полной суммы на
. И, наконец, для полной суммы на 
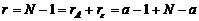 .
.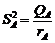 ,
, 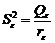 . (2.2.4)
. (2.2.4)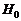 – все групповые выборки получены из одной нормальной совокупности;
– все групповые выборки получены из одной нормальной совокупности;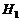 (альтернатива) – групповые выборки получены из нормальных совокупностей с одной генеральной дисперсией, но с разными генеральными средними.
(альтернатива) – групповые выборки получены из нормальных совокупностей с одной генеральной дисперсией, но с разными генеральными средними.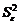 будем иметь
будем иметь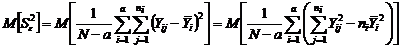 .
.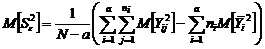 .
.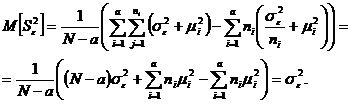
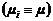 . Таким образом, приходим к выводу, что
. Таким образом, приходим к выводу, что 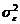 .
.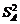 для
для 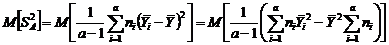 .
.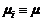 , получаем
, получаем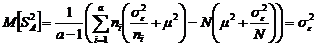 . (2.2.5)
. (2.2.5)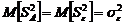 .
.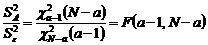 . (2.2.6)
. (2.2.6)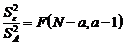 .
.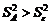 , и поскольку исторически сложилась практика оценки правдоподобия
, и поскольку исторически сложилась практика оценки правдоподобия 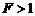 , в литературе дисперсионное отношение фигурирует в виде (2.2.6). Возможно будет уместным замечание более общего характера о том, что в любом прикладном статистическом анализе никогда не следует отождествлять объект исследования с априорными вероятностными схемами, положенными в основу модели. В противном случае, как это не парадоксально звучит, в погоне за точностью можно не только потерять адекватность модели, но и вовсе прийти к абсурдным результатам и выводам. Впрочем, при ближайшем рассмотрении, никакого парадокса здесь нет, и это обстоятельство является естественным следствием специфики стохастических закономерностей.
, в литературе дисперсионное отношение фигурирует в виде (2.2.6). Возможно будет уместным замечание более общего характера о том, что в любом прикладном статистическом анализе никогда не следует отождествлять объект исследования с априорными вероятностными схемами, положенными в основу модели. В противном случае, как это не парадоксально звучит, в погоне за точностью можно не только потерять адекватность модели, но и вовсе прийти к абсурдным результатам и выводам. Впрочем, при ближайшем рассмотрении, никакого парадокса здесь нет, и это обстоятельство является естественным следствием специфики стохастических закономерностей. 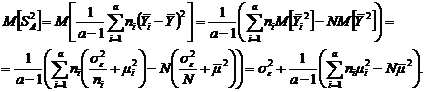
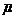 находим по правилу суперпозиции (п.1.2):
находим по правилу суперпозиции (п.1.2):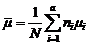 . (2.2.7)
. (2.2.7)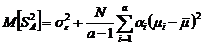 , (2.2.8)
, (2.2.8)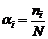 - парциальная доля
- парциальная доля 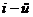 группы. Сумму во втором слагаемом (2.2.8) естественно интерпретировать как «дисперсию эффекта фактора»:
группы. Сумму во втором слагаемом (2.2.8) естественно интерпретировать как «дисперсию эффекта фактора»: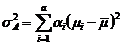 . (2.2.9)
. (2.2.9)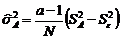 . (2.2.10)
. (2.2.10)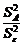 и сравнивается с правой 5% точкой статистики Фишера – с квантилью
и сравнивается с правой 5% точкой статистики Фишера – с квантилью 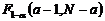 . Если выполняется условие
. Если выполняется условие 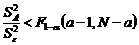 , то
, то 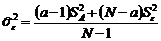 ;
;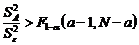 , то более правдоподобной признается альтернативная гипотеза
, то более правдоподобной признается альтернативная гипотеза 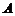 и
и 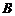 варьируются на
варьируются на 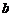 уровнях соответственно. В каждой из
уровнях соответственно. В каждой из 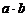 элементарных ячеек содержится
элементарных ячеек содержится 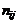 индивидуальных значений отклика. В дальнейшем, чтобы избежать громоздких формул, примем непринципиальное ограничение
индивидуальных значений отклика. В дальнейшем, чтобы избежать громоздких формул, примем непринципиальное ограничение 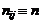 . Каждое индивидуальное значение теперь будет иметь 3 индекса:
. Каждое индивидуальное значение теперь будет иметь 3 индекса: 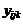 , где
, где 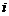 - номер уровня фактора
- номер уровня фактора 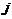 - фактора
- фактора 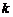 - порядковый номер внутри ячейки. Как и в однофакторном случае, средний результат по ячейке
- порядковый номер внутри ячейки. Как и в однофакторном случае, средний результат по ячейке 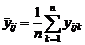 дает оценку отклика на пересечении уровней
дает оценку отклика на пересечении уровней 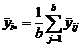 ;
; 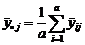 .
.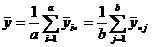 ,
,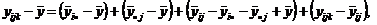 (2.2.11)
(2.2.11)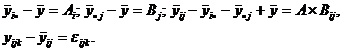
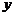 - выход продукта, а
- выход продукта, а 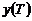 , а
, а 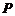 интерпретируем как параметр.
интерпретируем как параметр.

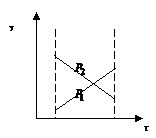
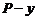 , когда
, когда 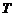 будет служить параметром.
будет служить параметром.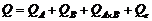 , (2.2.12)
, (2.2.12)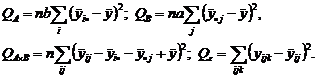 (2.2.13)
(2.2.13)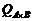 при фиксированном
при фиксированном 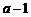 уравнений, образующихся при других значениях
уравнений, образующихся при других значениях 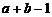 уравнений. Таким образом, для взаимодействия число степеней свободы составит:
уравнений. Таким образом, для взаимодействия число степеней свободы составит: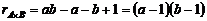 . (2.2.14)
. (2.2.14)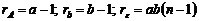 . (2.2.15)
. (2.2.15)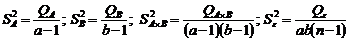 . (2.2.16)
. (2.2.16)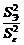 .
.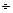 (2.2.13), остаются справедливыми. Основное отличие заключается в том, что резко возрастает количество взаимодействий высших порядков. В силу коммутативности взаимодействий
(2.2.13), остаются справедливыми. Основное отличие заключается в том, что резко возрастает количество взаимодействий высших порядков. В силу коммутативности взаимодействий 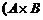 ~
~ 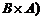 количество взаимодействий кратности
количество взаимодействий кратности 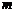 в
в 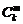 . Парных взаимодействий будет
. Парных взаимодействий будет 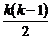 , тройных
, тройных 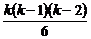 и т.д. Таким образом, структу-
и т.д. Таким образом, структу- 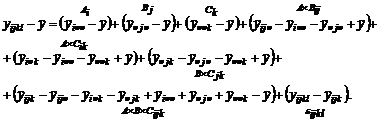 (2.2.17)
(2.2.17)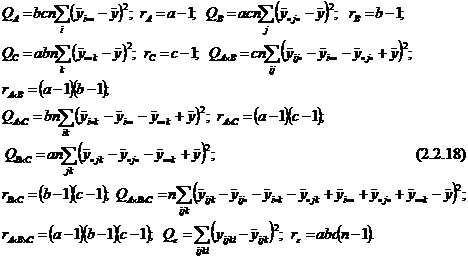
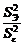 .
.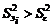 ), а остальные смешиваются со случайной ошибкой так же, как в однофакторной схеме. При этом в качестве более правдоподобной принимается альтернатива
), а остальные смешиваются со случайной ошибкой так же, как в однофакторной схеме. При этом в качестве более правдоподобной принимается альтернатива 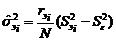 . В сущности говоря, этот факт есть прямое следствие правила вычисления дисперсии суперпозиции (вероятностной смеси) СВ, рассмотренного в п.1.2. Оценкой дисперсии полной изменчивости будет сумма всех парциальных дисперсий, включая дисперсию случайной ошибки:
. В сущности говоря, этот факт есть прямое следствие правила вычисления дисперсии суперпозиции (вероятностной смеси) СВ, рассмотренного в п.1.2. Оценкой дисперсии полной изменчивости будет сумма всех парциальных дисперсий, включая дисперсию случайной ошибки: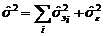 , (2.2.19)
, (2.2.19)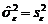 . Ранжировать эффекты и взаимодействия, признанные значимыми по результатам эксперимента, целесообразно по величине удельной доли соответствующей парциальной дисперсии:
. Ранжировать эффекты и взаимодействия, признанные значимыми по результатам эксперимента, целесообразно по величине удельной доли соответствующей парциальной дисперсии: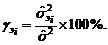 (2.2.20)
(2.2.20)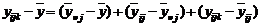 . (2.3.1)
. (2.3.1)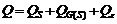 , (2.3.2)
, (2.3.2)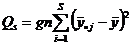 ;
; 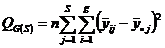 ;
; 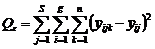 . (2.3.3)
. (2.3.3)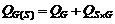 ,
, 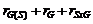 , (2.3.4)
, (2.3.4)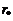 – число степеней свободы парциальной суммы квадратов. Результаты вычислений по (2.3.3) сведены в таблицу дисперсионного анализа (табл. 2.3.2).
– число степеней свободы парциальной суммы квадратов. Результаты вычислений по (2.3.3) сведены в таблицу дисперсионного анализа (табл. 2.3.2).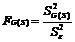 ). Если эффект оказывается незначимым, то его следует смешать с ошибкой, объединив строки «ε» и «G(S)» в строку «ε» по вышеизложенному алгоритму. Если же эффект оказывается значимым, то мерой для оценки значимости изменчивости между станками будет изменчивость между головками одного станка (
). Если эффект оказывается незначимым, то его следует смешать с ошибкой, объединив строки «ε» и «G(S)» в строку «ε» по вышеизложенному алгоритму. Если же эффект оказывается значимым, то мерой для оценки значимости изменчивости между станками будет изменчивость между головками одного станка ( 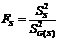 ).
).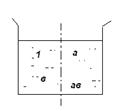
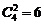 пар проб можно составлять 3 различных блока по 2 непересекающиеся пары проб, как показано в табл. 2.3.3.
пар проб можно составлять 3 различных блока по 2 непересекающиеся пары проб, как показано в табл. 2.3.3.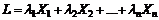 , (2.3.5)
, (2.3.5)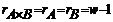
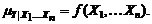 (2.4.1)
(2.4.1)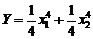 (2.4.2)
(2.4.2)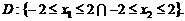
 .00
.00