
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Выборочные оценки параметров распределения1.При практическом применении статистических методов для анализа качества продукции, стабильности и точности технологических и измерительных процессов чаще всего приходится иметь дело со статистическим материалом ограниченного объема - 10÷100 измерений, либо сериями 5÷25 проб - малых выборок по 3÷7 измерений. Такого ограниченного материала недостаточно, чтобы найти заранее неизвестный закон распределения, хотя можно определить его важнейшие числовые характеристики: среднее и дисперсию либо параметры априорно известного закона распределения. Оценкой неизвестного параметра θ называется СВ, представляющая собой функцию выборочных значений В качестве оценки математического ожидания Несмещенная выборочная оценка дисперсии, как известно, имеет вид
Однако выборочное СКО Поскольку Это отрицательное смещение оценки s при выборках небольшого объема может приводить к заниженной оценке средней ширины зоны рассеивания процесса, приводя тем самым к завышенной оценке числовых индексов (Ср, Срк и т.д.). 2. Для установления ПР величин
Внося 
Величина
Среднее
Числовые характеристики выборочной дисперсии соответственно составят:
Для нормированного выборочного СКО Рассмотрим структуру последовательности
Первое слагаемое равно 0. Второе слагаемое подстановкой
Заменяя в рекуррентном соотношении (1.4.7)
Таким образом, несмещенную точечную выборочную оценку СКО получим, устранив отрицательное смещение М[S] тем же приемом, что и для s2:
В табл. 1.4.1 приведена величина относительной ошибки Таблица 1.4.1
3. Эффективность полученной оценки будет определяться дисперсией СВ
и при больших n имеет место асимптотика
Можно указать еще один способ вычисления
Точные значения 4. Другой способ получения оценок параметров распределения основан на порядковых статистиках. Рассмотрим выборку непрерывной СВ объемом n, полученную при стандартных условиях из совокупности с ФР Выборка, упорядоченная по возрастанию Используем универсальное автопреобразование
Рис.1.4.1. Схема расположения вариационного ряда выборки из совокупности R(0,1)
Вариационный ряд Таким образом, функция распределения Дифференцируя последнее выражение по
или, используя свойство биномиальных коэффициентов
В частности, для крайних членов вариационного ряда плотность распределения получаем, полагая
и В статистических приложениях большее распространение получили не сами элементарные порядковые статистики, а их композиции. Главным образом это размах Для установления законов распределения размаха и медианы необходимо знать закон совместного распределения двух элементарных порядковых статистик. Пусть их номера
Рис. 1.4.2. Схема расположения вариационного ряда выборки из совокупности
Рис. 1.4.3. Схема области интегрирования для определения закона совместного распределения двух порядковых статистик
Функцию совместного распределения двух порядковых статистик получаем в виде:
Дифференцируя
Эту схему рассуждений очевидно можно экстраполировать на любое количество членов вариационного ряда, и ПР совместного распределения всех членов вариационного ряда будет иметь вид
5.Закон распределения выборочного размаха найдем как частный случай разности между двумя членами вариационного ряда:
где Рассмотрим два частных случая:
Полагая в (1.4.17), (1.4.19)
Статистика При оговоренных условиях
Для
Рис. 1.4.4. Плотность выборочного размаха в зависимости от объема выборки
Асимптотика числовых характеристик нормированного размаха
При этом нормированный размах
Сравнительная эффективность оценки 6.При установлении закона распределения выборочной медианы рассмотрим два случая:
В этом случае
Для совокупности N(0,1) получаем
Для нормальной совокупности окончательно получаем
При n=2 медиана совпадает с выборочным средним. Вид ПР медианы для n=3÷5 представлен на рис.1.4.5.
Рис. 1.4.5. Плотность распределения выборочной медианы в зависимости от объема выборки n
При больших n для серединной порядковой статистики справедлива асимптотика
Таким образом, серединная порядковая статистика является асимптотически нормальной оценкой генеральной квантили Сравнительная эффективность оценки генерального среднего нормальной совокупности по выборочной медиане в зависимости от n приведена в табл. 1.4.2.
Таблица 1.4.2.Сравнительная эффективность точечных оценок параметров нормального распределения
Окончание табл. 1.4.2.
*) Символы **) В последней строке приведен асимптотический вид СКО соответствующих статистик при больших Приведенные в табл. 1.4.2 СКО используются, в частности, для определения контрольных границ при построении контрольных карт количественного признака (умножением на 3).
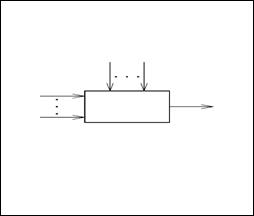
Глава 2. основы теории планирования эксперимента Факторы эксперимента. Понятие об эффекте фактора 1. Под экспериментом в контексте данного раздела будем понимать получение данных об исследуемом объекте в процессе многократной реализации искусственно созданной или контролируемой и неограниченно воспроизводимой совокупности внешних условий. Схематично модель системы «объект-эксперимент» можно представить, как показано на рис. 2.1.1.
ИО
Рис. 2.1.1. Кибернетическая модель исследуемого объекта
Основоположником планирования эксперимента принято считать английского математика Р. Фишера, который в своей работе «Планирование эксперимента и его статистическая основа» сформулировал основные принципы использования аппарата дисперсионного анализа для обработки результатов и оптимизации сельскохозяйственных экспериментов, главным образом, в растениеводстве. В связи с этим, сформировавшаяся в планировании эксперимента терминология во многом сохранила отпечаток этого исторически первого объекта исследования, как, например, «планы с расщепленными делянками», «эффект способа обработки», «эффект дозы» и т.д. Специфика данного объекта очевидно такова, что конечный результат – урожай (Y на рис. 2.1.1) – зависит, как правило, от множества внешних условий – факторов (Хiна рис.2.1.1): сорт растений, состав почвы, агротехнические приемы и т.д. Кроме того, влияние оказывают погодно-климатические и другие неподдающиеся управлению и контролю воздействия – случайные факторы (Zk на рис. 2.1.1). Другими немаловажными обстоятельствами являются принципиальная ограниченность в объеме исходного статистического материала и то, что для повторения эксперимента необходимо ждать как минимум год. Таким образом, вероятностной моделью в планировании эксперимента является интерпретация зависимости Y(X1,...Xn) как стохастической. Причем, задача установления причинно-следственных связей, т.е. какого-либо естественно-научного механизма в данной зависимости, изначально не рассматривалась в качестве осуществимой, как, например, в статистической физике. Доказав свою эффективность в сельском хозяйстве, математическое планирование эксперимента стало с успехом применяться в биологии, медицине, а затем при оптимизации технологических и других производственных процессов. Такой подход к исследованию многофакторных систем получил название кибернетического (безотносительно природы причинно-следственных связей). Таким образом, основные исходные понятия планирования эксперимента заключаются в следующем. Факторы эксперимента (или просто факторы) – входные параметры системы, непосредственно формирующие выходной параметр – отклик. Откликов, вообще говоря, может быть несколько, но в дальнейшем ограничимся рассмотрением ситуации с одним. Основные требования к факторам: · измеримость – возможность непосредственной количественной оценки; · возможность контролирования постоянного значения (на фиксированном уровне) в процессе единичной реализации эксперимента; · априорная взаимная независимость. Факторы подразделяются на два типа: · Факторы с количественными уровнями (температура, давление, ток и т.д.). · Факторы с альтернативными уровнями, т.е. такие, которые можно лишь пронумеровать натуральными числами (способы обработки, индивидуальные технологические линии, контролеры-операторы и т.д.). К отклику предъявляется по существу единственное требование – однозначная измеримость. 2. Помимо факторов на формирование отклика оказывают влияние и другие входные параметры, остающиеся вне поля зрения экспериментатора (Z на рис. 2.1.1). Поэтому существует опасность ошибочной интерпретации результатов эксперимента, так называемого «ложного эффекта», когда флуктуация неконтролируемых входных параметров приводит к значимому изменению отклика и воспринимается как результат воздействия факторов. Эта проблема особенно актуальна при проведении серии параллельных испытаний (повторении откликов) на всех или нескольких сочетаниях уровней факторов. Для сведения к минимуму возможности подобных ошибок применяется рандомизация – установление случайной очередности реализации индивидуальных опытов. Например, если единственный фактор варьируется на четырех уровнях, и на каждом уровне проводится серия из двух повторных испытаний, то очередность осуществления восьми индивидуальных испытаний определяется случайной последовательностью натуральных чисел 1 3. Совокупность исходных данных, полученных в процессе эксперимента, представляет собой выборку, расслоенную на группы (подвыборки). Группообразующим признаком является постоянство сочетания уровней факторов, при котором были получены индивидуальные значения. Такая группа образует элементарную ячейку эксперимента. В различных ячейках может содержаться, вообще говоря, неодинаковое число значений. В вырожденном случае ячейка может содержать одно значение. Условимся факторы обозначать заглавными буквами A, B, C,…, а прописными a, b, c,…- количество уровней соответствующего фактора. Количество ячеек при этом очевидно составит a Представим для наглядности структуру результатов однофакторного эксперимента, где фактор А варьируется на а уровнях, в виде табл. 2.1.1.
Таблица 2.1.1. Структура результатов однофакторного эксперимента
Столбцы в табл. 2.1.1 являются элементарными ячейками с Внутригрупповую изменчивость Таким образом, полную изменчивость индивидуальных значений можно представить в виде суммы двух компонент: эффекта фактора и случайной ошибки:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
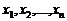 :
: 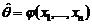 , вид которой определяется, исходя из «физического смысла» параметра θ и информации о законе распределения СВ X.
, вид которой определяется, исходя из «физического смысла» параметра θ и информации о законе распределения СВ X.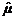 чаще всего используется выборочное среднее:
чаще всего используется выборочное среднее: 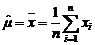 .Числовые характеристики
.Числовые характеристики 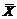 равны:
равны: 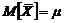 ,
, 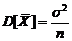 .
.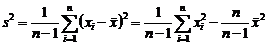 .
.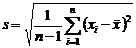 не является несмещенной оценкой параметра
не является несмещенной оценкой параметра  . В этом легко убедиться, рассмотрев дисперсию s:
. В этом легко убедиться, рассмотрев дисперсию s: 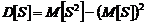 .
.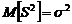 , приходим к очевидному выводу, что
, приходим к очевидному выводу, что  .
.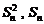 и определения несмещенной оценки
и определения несмещенной оценки 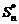 рассмотрим нормированную сумму квадратов отклонений:
рассмотрим нормированную сумму квадратов отклонений: 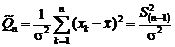 . Используя тождественное преобразование, представим
. Используя тождественное преобразование, представим 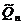 в следующем виде:
в следующем виде: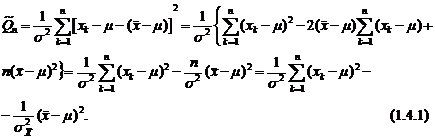
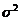 и
и 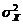 под знак квадрата, убеждаемся, что каждое из слагаемых представляет собой СВ
под знак квадрата, убеждаемся, что каждое из слагаемых представляет собой СВ 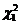 - квадрат стандартной нормальной СВ. Перепишем (1.4.1) в виде
- квадрат стандартной нормальной СВ. Перепишем (1.4.1) в виде 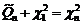 . Поскольку
. Поскольку 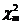 аддитивна по степеням свободы (
аддитивна по степеням свободы ( 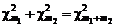 ), приходим к выводу, что
), приходим к выводу, что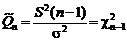 . (1.4.2)
. (1.4.2)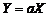 (
( 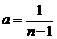 ), найдем ПР
), найдем ПР 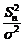 :
: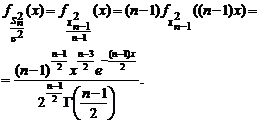 (1.4.3)
(1.4.3)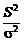 равно 1. Дисперсию найдем, используя соотношение
равно 1. Дисперсию найдем, используя соотношение 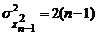 и формулу для дисперсии нормированной СВ
и формулу для дисперсии нормированной СВ 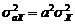 . Полагая
. Полагая 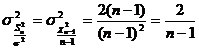 . (1.4.4)
. (1.4.4)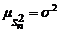 ,
, 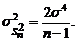 (1.4.5)
(1.4.5)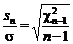 ПР найдем, используя преобразование
ПР найдем, используя преобразование 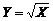 :
: 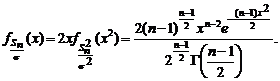 (1.4.6)
(1.4.6)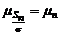 . Для
. Для 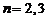
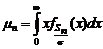 легко вычисляются и составляют:
легко вычисляются и составляют: 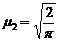 ,
, 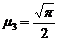 . Рассмотрим случай n > 3:
. Рассмотрим случай n > 3: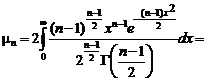
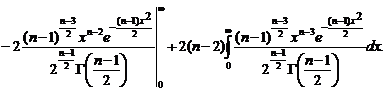
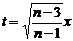 , используя рекуррентное свойство
, используя рекуррентное свойство 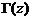 , преобразуем к виду
, преобразуем к виду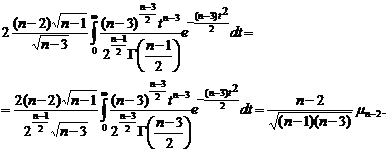 (1.4.7)
(1.4.7)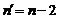 (
( 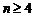 ) и используя рекуррентное свойство Гамма-функции, по индукции получаем формулу общего члена последовательности
) и используя рекуррентное свойство Гамма-функции, по индукции получаем формулу общего члена последовательности 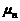 :
: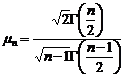 ,
,  . (1.4.8)
. (1.4.8)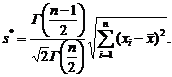 (1.4.9)
(1.4.9)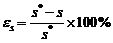 в зависимости от объема выборки.
в зависимости от объема выборки.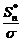 :
: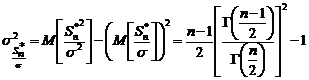 , (1.4.10)
, (1.4.10)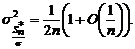
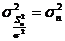 . Внося
. Внося 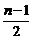 в (1.4.10) под знак квадрата и используя рекуррентное свойство
в (1.4.10) под знак квадрата и используя рекуррентное свойство 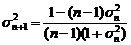 ,
, 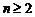 ,
, 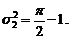 (1.4.11)
(1.4.11)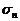 приведены в табл. 1.4.2 в столбце
приведены в табл. 1.4.2 в столбце 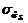 .
.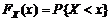 и ПР
и ПР 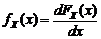 :
: 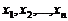 .
.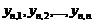
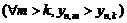 , называется вариационным рядом. Член вариационного ряда с фиксированным номером
, называется вариационным рядом. Член вариационного ряда с фиксированным номером 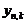 называется элементарной порядковой статистикой. Каждому номеру
называется элементарной порядковой статистикой. Каждому номеру 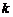
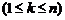 соответствует случайная величина
соответствует случайная величина 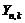 с законом распределения, зависящим от
с законом распределения, зависящим от 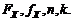 Основным исходным пунктом при установлении закона распределения
Основным исходным пунктом при установлении закона распределения 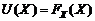 (п.1.2) и рассмотрим вариационный ряд
(п.1.2) и рассмотрим вариационный ряд 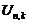 , все члены которого будут сосредоточены на отрезке [0;1] (рис.1.4.1).
, все члены которого будут сосредоточены на отрезке [0;1] (рис.1.4.1).
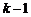 значение, меньшее
значение, меньшее 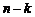 значений, больших
значений, больших 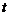
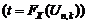 . Тогда вероятность того, что
. Тогда вероятность того, что 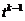 , вероятность того, что
, вероятность того, что 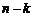 значений окажется правее точки
значений окажется правее точки 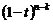 . Вероятность всей композиции будет равна произведению
. Вероятность всей композиции будет равна произведению 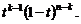 Количество комбинаций, реализующих точное расположение, согласно формуле полиномиального распределения (см. ссылку. на стр. 7), составит
Количество комбинаций, реализующих точное расположение, согласно формуле полиномиального распределения (см. ссылку. на стр. 7), составит 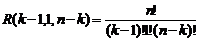 .
.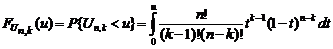 . (1.4.12)
. (1.4.12)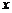 и вспоминая, что
и вспоминая, что 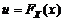 ,
, 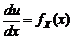 , получаем плотность распределения
, получаем плотность распределения 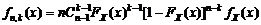 , (1.4.13)
, (1.4.13)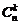 , получаем тождественную форму:
, получаем тождественную форму: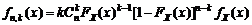 . (1.4.14)
. (1.4.14)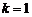 - для минимального:
- для минимального: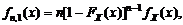 (1.4.15)
(1.4.15)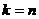 - для максимального:
- для максимального: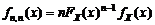 . (1.4.16)
. (1.4.16)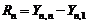 и медиана выборки четного объема
и медиана выборки четного объема 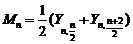 , представляющие собой соответственно разность и сумму двух членов вариационного ряда (медианой выборки нечетного объема служит статистика
, представляющие собой соответственно разность и сумму двух членов вариационного ряда (медианой выборки нечетного объема служит статистика 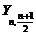 ).
). 
 . Как и в предыдущем случае, применим универсальное автопреобразование
. Как и в предыдущем случае, применим универсальное автопреобразование 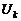 окажется разбитым на 5 групп (рис. 1.4.2) численностью
окажется разбитым на 5 групп (рис. 1.4.2) численностью 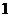 ,
, 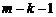 , 1,
, 1, 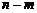 соответственно.
соответственно.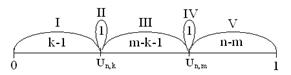
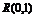 с двумя фиксированными членами
с двумя фиксированными членами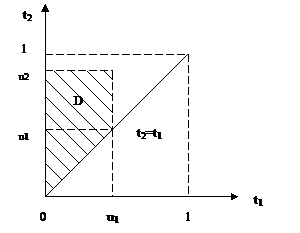
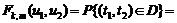
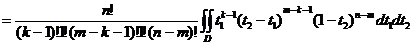 .
.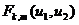 по
по 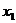 и
и 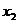 и учитывая, что
и учитывая, что 
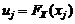 ,
, 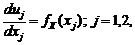 окончательно получаем плотность распределения
окончательно получаем плотность распределения 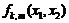 в виде
в виде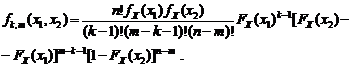 (1.4.17)
(1.4.17)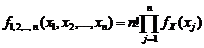 ,
, 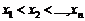 . (1.4.18)
. (1.4.18)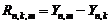 ,
, 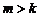 . Плотность распределения разности двух случайных величин имеет вид
. Плотность распределения разности двух случайных величин имеет вид 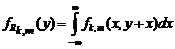 ,
, 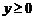 , (1.4.19)
, (1.4.19) 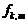 –ПР совместного распределения (1.4.17).
–ПР совместного распределения (1.4.17). межвариационный (последовательный) размах. Полагая в (1.4.19)
межвариационный (последовательный) размах. Полагая в (1.4.19) 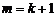 ,
, 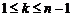 , получаем
, получаем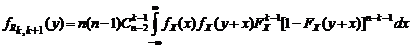 ,
,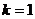 ,
, 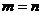 , получаем
, получаем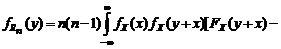
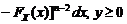 . (1.4.21)
. (1.4.21)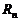 выборки из нормальной совокупности является одной из наиболее популярных, поэтому рассмотрим ПР
выборки из нормальной совокупности является одной из наиболее популярных, поэтому рассмотрим ПР 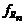 более детально. Как обычно в подобных случаях, рассмотрим совокупность
более детально. Как обычно в подобных случаях, рассмотрим совокупность 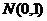 , поскольку
, поскольку 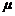 не зависит, а при произвольном
не зависит, а при произвольном 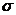 размаха выборки из
размаха выборки из 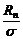 выборки из произвольной нормальной совокупности).
выборки из произвольной нормальной совокупности).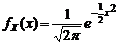 ,
, 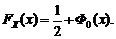 Подставляя
Подставляя 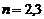 в (1.4.21), находим:
в (1.4.21), находим: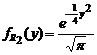 ,
, 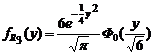 . (1.4.22)
. (1.4.22)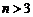 точные формулы ПР существуют только в квадратуре и для больших
точные формулы ПР существуют только в квадратуре и для больших 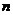 нужно исследовать их асимптотическое поведение. Вид ПР
нужно исследовать их асимптотическое поведение. Вид ПР 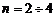 , 10 представлен на рис. 1.4.4.
, 10 представлен на рис. 1.4.4.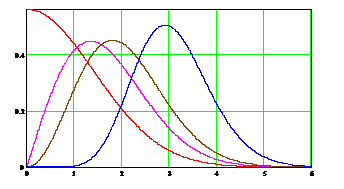
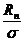 имеет вид
имеет вид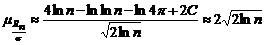 ,
, 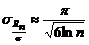 . (1.4.23)
. (1.4.23)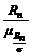 , очевидно, есть несмещенная оценка генерального СКО, т.е.
, очевидно, есть несмещенная оценка генерального СКО, т.е. 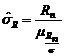 . В свою очередь, СКО полученной оценки будет совпадать с коэффициентом вариации нормированного размаха
. В свою очередь, СКО полученной оценки будет совпадать с коэффициентом вариации нормированного размаха 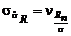 , предельное значение которого составит
, предельное значение которого составит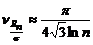 . (1.4.24)
. (1.4.24)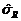 приведена в табл. 1.4.2. Числовые характеристики и квантили нормированного размаха
приведена в табл. 1.4.2. Числовые характеристики и квантили нормированного размаха  медиана выборки нечетного объема.
медиана выборки нечетного объема.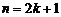 , и медианой служит серединная порядковая статистика с номером
, и медианой служит серединная порядковая статистика с номером 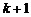 . Подставляя параметры статистики
. Подставляя параметры статистики 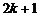 ,
, 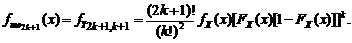 (1.4.25)
(1.4.25)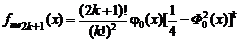 ; (1.4.26)
; (1.4.26)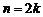 в качестве медианы, вообще говоря, может рассматриваться любая точка из интервала
в качестве медианы, вообще говоря, может рассматриваться любая точка из интервала 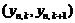 . Для определенности медианой принято считать середину указанного интервала. Плотность распределения случайной величины
. Для определенности медианой принято считать середину указанного интервала. Плотность распределения случайной величины 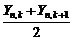 найдем путем последовательных преобразований. Сначала найдем плотность распределения суммы, используя формулу суммы и ПР (1.4.14) и учитывая, что
найдем путем последовательных преобразований. Сначала найдем плотность распределения суммы, используя формулу суммы и ПР (1.4.14) и учитывая, что  :
: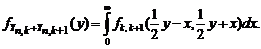 Искомую ПР медианы получим из ПР суммы:
Искомую ПР медианы получим из ПР суммы: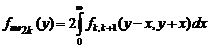 . (1.4.27)
. (1.4.27)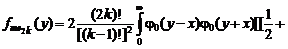
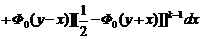 . (1.4.28)
. (1.4.28)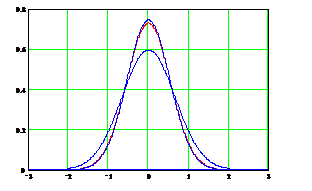
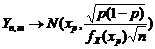 , где
, где 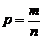 . (1.4.29)
. (1.4.29)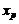
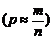 при любом законе распределения
при любом законе распределения 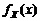 . В частности, для нормальной совокупности
. В частности, для нормальной совокупности 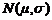 выборочная медиана распределена по нормальному закону
выборочная медиана распределена по нормальному закону 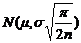 , являясь несмещенной оценкой генерального среднего. При этом оценка по медиане при больших n в
, являясь несмещенной оценкой генерального среднего. При этом оценка по медиане при больших n в 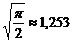 раз менее эффективна, чем по выборочному среднему, у которого
раз менее эффективна, чем по выборочному среднему, у которого 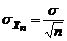 .
.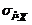 *)
*)
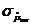
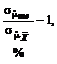
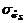
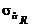
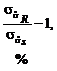
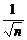
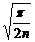
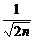
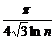
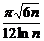
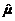 ,
, 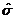 означают несмещенные выборочные оценки генеральных параметров, индексы соответствуют используемой статистике.
означают несмещенные выборочные оценки генеральных параметров, индексы соответствуют используемой статистике.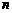 .
.
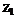
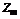
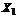
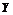
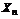
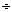 8, получаемой с помощью генератора случайных чисел. «Физически» этот процесс можно представить как случайную выборку без возвращения восьми пронумерованных шаров из лототрона. В результате рандомизации возможные флуктуации неконтролируемых факторов равномерно распределяются по всей совокупности индивидуальных значений отклика и проявляют себя как увеличение случайной ошибки (погрешности) эксперимента.
8, получаемой с помощью генератора случайных чисел. «Физически» этот процесс можно представить как случайную выборку без возвращения восьми пронумерованных шаров из лототрона. В результате рандомизации возможные флуктуации неконтролируемых факторов равномерно распределяются по всей совокупности индивидуальных значений отклика и проявляют себя как увеличение случайной ошибки (погрешности) эксперимента.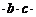 …, в каждой из которых содержится
…, в каждой из которых содержится 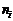 индивидуальных значений. И, наконец, общее количество индивидуальных значений
индивидуальных значений. И, наконец, общее количество индивидуальных значений 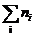 условимся обозначать N.
условимся обозначать N.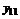
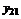
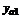
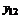
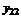
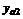
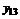
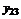
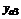
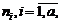 индивидуальными значениями в каждой. В качестве наилучшей оценки значения отклика на i-м уровне фактора естественно принять групповые средние
индивидуальными значениями в каждой. В качестве наилучшей оценки значения отклика на i-м уровне фактора естественно принять групповые средние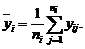 (2.1.1)
(2.1.1)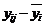 , поскольку она не обусловлена никакими контролируемыми воздействиями, естественно интерпретировать как случайную ошибку эксперимента. Для оценки контролируемой изменчивости единственно возможным началом отсчета является общий средний результат
, поскольку она не обусловлена никакими контролируемыми воздействиями, естественно интерпретировать как случайную ошибку эксперимента. Для оценки контролируемой изменчивости единственно возможным началом отсчета является общий средний результат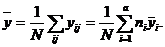 (2.1.2)
(2.1.2)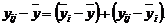 . (2.1.3)
. (2.1.3)