
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон совместного распределения выборочных значений1. Все множество объектов, из которого производится их случайный равновероятный отбор, или, в терминах случайной величины, множество всех ее возможных значений, называется генеральной совокупностью. Группа из конечного числа
В случае непрерывной СВ аналогичное соотношение справедливо и для плотности совместного распределения:
При этом, поскольку все выборочные значения равновероятны с вероятностью 
Так как величины
2. Чтобы прояснить смысл соотношений (1.3.3), (1.3.4), рассмотрим следующий пример. Пусть X — стандартная нормальная СВ Свертка (1.3.3) дает следующий результат:
Выборочное среднее в данном случае имеет нормальное распределение с параметрами Математическая статистика решает как бы «обратную задачу» теории вероятностей. То есть, если при классическом определении случайного события и вероятности по известным характеристикам генеральной совокупности вычислялись вероятности выборочных значений (результатов независимых испытаний), то в практических приложениях, наоборот, по имеющимся в распоряжении «наблюденным» выборочным значениям оцениваются неизвестные числовые характеристики и законы распределения генеральной совокупности. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 368. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
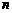 объектов, охваченных обследованием, называется случайной выборкой, или просто - выборкой, а их количество
объектов, охваченных обследованием, называется случайной выборкой, или просто - выборкой, а их количество 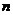 - объемом выборки. Выборка называется репрезентативной (представительной), если она достаточно точно повторяет пропорции генеральной совокупности. В вероятностной интерпретации набор выборочных значений
- объемом выборки. Выборка называется репрезентативной (представительной), если она достаточно точно повторяет пропорции генеральной совокупности. В вероятностной интерпретации набор выборочных значений 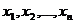 представляет собой
представляет собой 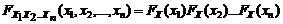 . (1.3.1)
. (1.3.1)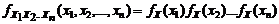 . (1.3.2)
. (1.3.2)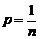 , выборочное среднее, определяемое как среднее арифметическое
, выборочное среднее, определяемое как среднее арифметическое 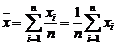 , представляет собой СВ
, представляет собой СВ 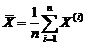 (n - кратную композицию величины
(n - кратную композицию величины 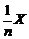 с самой собой). Плотность распределения выборочного среднего можно получить, воспользовавшись тем, что СВ
с самой собой). Плотность распределения выборочного среднего можно получить, воспользовавшись тем, что СВ 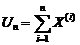 имеет ПР, представляющую собой
имеет ПР, представляющую собой 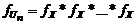 . (1.3.3)
. (1.3.3)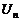 и
и 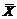 связаны линейным соотношением, то на основании правила линейного преобразования (п. 1.1.) получим
связаны линейным соотношением, то на основании правила линейного преобразования (п. 1.1.) получим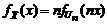 . (1.3.4)
. (1.3.4)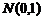 . Выборка объемом
. Выборка объемом 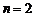 представляет собой две независимых СВ
представляет собой две независимых СВ 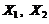 с плотностью совместного распределения
с плотностью совместного распределения 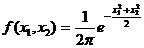 .
.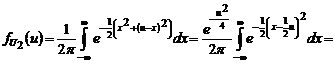
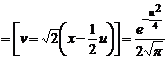 . Совершив второе преобразование путем деления на 2, находим
. Совершив второе преобразование путем деления на 2, находим 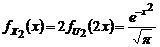 .
.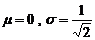 . С увеличением объема выборки из
. С увеличением объема выборки из 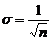 . При распределениях, отличных от нормального, выборочное среднее, представляющее собой композицию нескольких СВ с одним законом распределения, достаточно быстро нормализуется с увеличением объема выборки. Этот факт, являющийся следствием центральной предельной теоремы, был проиллюстрирован в п.1.2
. При распределениях, отличных от нормального, выборочное среднее, представляющее собой композицию нескольких СВ с одним законом распределения, достаточно быстро нормализуется с увеличением объема выборки. Этот факт, являющийся следствием центральной предельной теоремы, был проиллюстрирован в п.1.2