Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модель функционирования измерительной системы1. Пусть
Априорное безусловное распределение (входного сигнала) будем полагать известным – fX(x). Тогда ПР совместного распределения согласно п.1.3 будет иметь вид
Закон распределения Y и ПР апостериорного условного распределения будут равны соответственно:
В качестве первого варианта модели рассмотрим нормальный закон распределения случайной ошибки. Положим, что погрешность имеет только случайную составляющую (систематическая устранена метрологическими приемами). Тогда плотность распределения (3.4.1) будет иметь вид
где sY - СКО случайной погрешности. Пусть входной сигнал Х так- же имеет нормальное распределение:
где sX – СКО входного сигнала. Среднее значение без ограничения общности принято за начало отсчета. Введем в рассмотрение отношение 
Подставляя (3.4.7) в (3.4.3), (3.4.4), после элементарных преобразований получим:
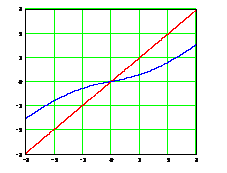
Как видно из последних выражений, результат измерения Однако более интересным результатом является то, что линия регрессии
Рис. 3.4.1. Линия регрессии и 6- сигмовая полоса измеряемого сигнала при v=0,3 в сравнении с идеальной линией x=y Таким образом, главный вывод состоит в том, что случайная компонента погрешности индуцирует систематическую составляющую погрешности. Эта составляющая («ножницы» между регрессией 2. В качестве другой модели случайной погрешности рассмотрим ошибку отсчета – округление показаний при считывании с градуированной шкалы измерительного прибора с ценой деления
Приняв распределение входного сигнала в том же виде (3.4.6) и проделав аналогичную предыдущему случаю цепочку вычислений, получим
В данном случае регрессия будет иметь вид
Нормируя все величины на
Вид зависимости (3.4.16) показан на рис.3.4.2.
Рис. 3.4.2. Регрессия точного значения на показания измерения при наличии ошибки отсчета h=0,1s; s |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 371. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
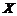 – истинное значение измеряемого параметра объекта (единицы продукции), случайного выбранного из некоторой со-вокупности, или истинное значение аналогового сигнала (напряжение, давление, температура и т.д.), поступающего на вход измерительного устройства. Результат измерения
– истинное значение измеряемого параметра объекта (единицы продукции), случайного выбранного из некоторой со-вокупности, или истинное значение аналогового сигнала (напряжение, давление, температура и т.д.), поступающего на вход измерительного устройства. Результат измерения 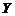 , вообще говоря, будет представлять собой случайную величину, отличную от
, вообще говоря, будет представлять собой случайную величину, отличную от 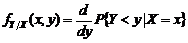 . (3.4.1)
. (3.4.1)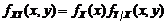 (3.4.2)
(3.4.2)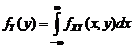 , (3.4.3)
, (3.4.3)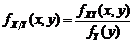 . (3.4.4)
. (3.4.4)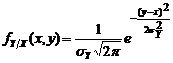 , (3.4.5)
, (3.4.5)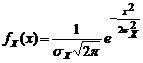 , (3.4.6)
, (3.4.6)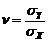 и переобозначим
и переобозначим 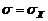 . В новых обозначениях ПР (3.4.2) примет вид
. В новых обозначениях ПР (3.4.2) примет вид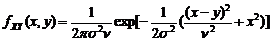 . (3.4.7)
. (3.4.7)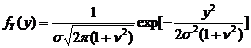 , (3.4.8)
, (3.4.8)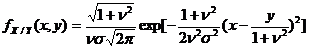 . (3.4.9)
. (3.4.9)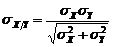 .
.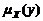 не совпадает с прямой
не совпадает с прямой 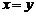 (рис. 3.4.1). Имеет место отрицательное смещение, линейно зависящее от
(рис. 3.4.1). Имеет место отрицательное смещение, линейно зависящее от 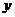 :
: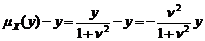 . (3.4.10)
. (3.4.10)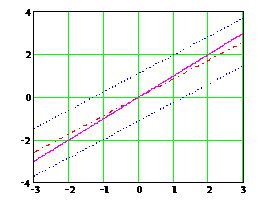
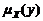 и главной биссектрисой, соответствующей идеальным измерениям) приводит к тому, что результат измерения Y завышает истинное значение Х и эта разница возрастает пропорционально удалению от центра рассеяния входного сигнала. Другой, парадоксальный на первый взгляд, вывод состоит в том, что коэффициент корреляции
и главной биссектрисой, соответствующей идеальным измерениям) приводит к тому, что результат измерения Y завышает истинное значение Х и эта разница возрастает пропорционально удалению от центра рассеяния входного сигнала. Другой, парадоксальный на первый взгляд, вывод состоит в том, что коэффициент корреляции 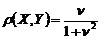 убывает до нуля по мере уменьшения среднеквадратичного отклонения случайной погрешности. Это является следствием того, что вместе с уменьшением рассеяния отклонения
убывает до нуля по мере уменьшения среднеквадратичного отклонения случайной погрешности. Это является следствием того, что вместе с уменьшением рассеяния отклонения 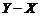 убывает и ковариация
убывает и ковариация 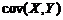 .
.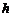 . В этом случае (3.4.1) будет иметь вид:
. В этом случае (3.4.1) будет иметь вид: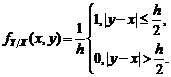 (3.4.11)
(3.4.11)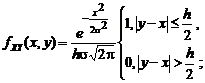 (3.4.12)
(3.4.12)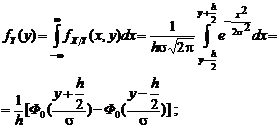 (3.4.13)
(3.4.13)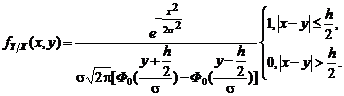 (3.4.14)
(3.4.14)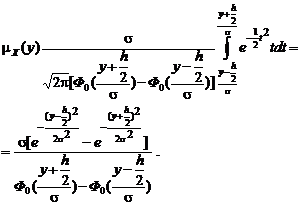 (3.4.15)
(3.4.15) и обозначив
и обозначив 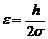 , приведем (3.4.15) к виду
, приведем (3.4.15) к виду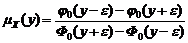 . (3.4.16)
. (3.4.16)