
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава 1. Теоретические основы статистического моделирования случайных процессовСтр 1 из 18Следующая ⇒ СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И СИСТЕМНЫЙ АНАЛИЗ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
САМАРА Издательство СГАУ 2008 УДК 519.21 ББК 22.171
Рецензенты: д-р физ.-мат. наук, проф. А. Ф. Крутов д-р техн. наук, проф. В. Д. Юшин
Плотников А. Н. П 396Статистическое моделирование и системный анализ технологических процессов: учеб. пособие / А. Н. Плотников. – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2008. – 155с.
ISBN 978 – 5 –7883 –0678 –2
Содержит краткое изложение вероятностных основ статистических методов в контексте их практического использования при анализе качества и надежности продукции машиностроительного производства. В главе1 излагаются общие вероятностные основы и рассмотрены наиболее употребительные выборочные статистики нормальных совокупностей, в том числе порядковые статистики. Основная часть посвящена системам случайных величин и типам их взаимодействий. В главе 2 даны основы дисперсионного анализа и теории планирования эксперимента. В главах 3-5 рассмотрены модели функционирования контрольных , измерительных процессов, основы теории массового обслуживания и схемы статистического регулирования технологических процессов. В качестве иллюстраций приведены примеры статистических экспериментов по методу Монте–Карло, реализованные в пакете Mathcad-2001, которые могут быть использованы для аудиторного и самостоятельного лабораторного практикума по различным приложениям теории вероятностей. Пособие предназначено для студентов специальностей «Стандартизация и сертификация» и «Управление качеством», а также других специальностей. 
УДК 519.21 ББК 22.171 ISBN 978 – 5 –7883 –0678 –2
© Плотников А. Н. © Самарский государственный аэрокосмический университет, 2008 ОГЛАВЛЕНИЕ
Введение..................................................................................................5
Глава 1. Теоретические основы статистического моделирования случайных процессов............................................................. 10 1.1. Преобразования случайных величин и сущность метода Монте‑Карло...........................................................10 1.2. Системы случайных величин..............................................13 1.3. Закон совместного распределения выборочных значений................................................................................27 1.4. Выборочные оценки параметров распределения..............30
Глава 2. Основы теории планирования эксперимента.......................44 2.1.Факторы эксперимента. Понятие об эффекте фактора….44 2.2. Аппарат дисперсионного анализа......................................48 2.3.Планы со смешиванием эффектови дробные многофакторные планы.......................................................58 2.4.Планы эксперимента для исследования поверхности отклика……………………………………….69
Глава 3. Системный анализ контрольных и измерительных процессов..................................................................................81 3.1. Модель функционирования системы контроля.................81 3.2. Принцип накопления и анализа информации. Оценка эффективности контроля.....................................................87 3.3. Сущность процесса измерения и основные элементы измерительной системы.......................................................92 3.4. Модель функционирования измерительной системы.......95 3.5. Модель функционирования измерительной системы при приемке по допуску.....................................................100
Глава 4. Основы теории надежности технологических и информационных систем...................................................102 4.1. Потоки случайных событий и их свойства......................102 4.2. Парадокс инспекции и смежные вопросы........................109 4.3. Очереди и задачи обслуживания.......................................112 4.4. Статистическая оценка параметра показательного закона...................................................................................122
Глава 5. Статистическое моделирование случайных процессов......125 5.1. Модели процессов с непрерывным приращением..........125 5.2. Анализ схем статистического регулирования ................129 5.3. Выборочные оценки числовых индексов воспроиз- водимости............................................................................138
Список литературы...............................................................................144
Приложения...........................................................................................145 Приложение I. Алгоритмы Монте-Карло, эксперементаль- ные и расчетные значения инвариантов структуры серий в последовательной выборке……………………………..…145 Приложение II. Таблица распределения Кохрэна.................151 Приложение III. Таблица распределения выборочного размаха................................................................................…..153
Введение 1. Исходным понятием теории вероятностей является случайное событие – событие, которое может произойти или не произойти при воспроизводимой совокупности условий опыта (испытания, наблюдения). Например, появление орла при бросании монеты, выпадение 11 очков при бросании двух игральных костей, попадание в поле допуска размера очередной детали с автоматической производственной линии, существенное улучшение состояния у группы больных после лечения определенным препаратом и т.д. Из перечисленных примеров видно, что каждое событие обладает некоторой степенью возможности. В примере с монетой и игральными костями сразу можно решить, что выпадение орла более возможно, чем выпадение 11 очков при бросании двух игральных костей, а для анализа стабильности технологического процесса или действия лекарственного препарата необходимо иметь фактические результаты наблюдений. С понятием случайного события связано другое фундаментальное понятие теории вероятностей – понятие случайной величины (СВ). Под случайной величиной понимается величина, которая в опыте с несколькими возможными исходами может принимать то или иное значение. Например, число очков при бросании игральной кости, частота появления «орла» в серии повторных опытов с монетой, фактическое количественное значение параметра при контроле и испытаниях промышленной продукции, очередной результат в серии повторных измерений и т.д. Законом распределения случайной величины называется любое правило (функция), позволяющее однозначно определить вероятности возможных значений случайной величины. Наиболее просто обстоит дело, когда множество возможных значений случайной величины конечно либо счетно и может быть отождествлено с пространством событий. Например, появление любого из чисел от «1» до «6» при бросании игральной кости равновероятно с вероятностью Очень важную роль при анализе CB играют ее числовые характеристики, позволяющие определить ее положение на числовой оси, величину рассеивания – степень случайности и форму рассеяния. Важнейшей числовой характеристикой CB является ее среднее значение или математическое ожидание, определяемой как Если под В механической интерпретации – среднее значение неслучайной величины а равно ей самой, – для любой пары CB Х и Y и неслучайных чисел a и b – дисперсия неслучайной величины a равна нулю, –для любой пары независимых CB 2.Наиболее употребительными являются следующие виды дискретных CB. Гипергеометрическое распределение в наглядной интерпретации представляет собой распределение числа черных шаров в случайной выборке или без возвращения из корзины (числа дефектных единиц при выборочном контроле партии штучной продукции). Это распределение совпадает с законом «Спорт-лото»
Биномиальное распределение. Рассмотрим асимптотику при
После группировки сомножителей и выделения
Откуда получаем асимптотику В чистом виде биноминальное распределение возникает в выборке с возвращением, когда вероятность успеха каждого испытания не зависит от результатов других испытаний и является величиной постоянной.Числовые характеристики биномиального распределения имеют вид: В предельном случае, когда количество опытов n в испытаниях неограниченно возрастает, а вероятность успеха q неограниченно убывает, но так, что их произведение Перепишем биномиальный закон в виде
Первые три сомножителя на основании второго замечательного предела дадут
Таким образом, для распределения числа редких событий получаем асимптотику в виде распределения Пуассона:
Помимо рассмотренного «предельного» случая, распределение Пуассона (распределение вероятностей редких событий) является одним из фундаментальных результатов во многих других приложениях теории вероятностей (теория надежности, теория случайных процессов и т.д.). У пуассоновской CB среднее и дисперсия равны между собой: 3. Муавр, а позднее независимо от него Лаплас исследовали биномиальное распределение при больших n и установили приближенную формулу (теорема Муавра-Лапласа):
При этом дискретные точки нормированной CB
а нижний предел в интеграле при больших Функция, стоящая под интегралом Функцию распределения CB или интеграл вероятностей, определяется уравнением Таким образом, можно осуществить переход от дискретных CB к непрерывным, важнейшей из которых является именно нормальная CB. Плотность распределения и числовые характеристики CB X, связанной с CB Z отношением X=sZ+m , имеют следующий вид:
Глава 1. Теоретические основы статистического моделирования случайных процессов |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 341. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; множество возможных значений частоты появления «орла» при трех бросаниях монеты составляет
; множество возможных значений частоты появления «орла» при трех бросаниях монеты составляет  с вероятностями
с вероятностями 
 .
.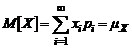 .
.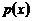 понимать дискретное распределение единичной массы на тонком невесомом стержне, то среднее значение можно интерпретировать как
понимать дискретное распределение единичной массы на тонком невесомом стержне, то среднее значение можно интерпретировать как 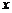 – координату центра масс такой системы. Рассеивание CB около своего среднего значения характеризуется дисперсией
– координату центра масс такой системы. Рассеивание CB около своего среднего значения характеризуется дисперсией 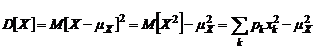 .
. есть момент инерции стержня переменной плотности относительно перпендикулярной оси, проходящей через точку
есть момент инерции стержня переменной плотности относительно перпендикулярной оси, проходящей через точку  . Для большей наглядности рассеивание CB характеризуют стандартным или средним квадратичным отклонением (СКО)
. Для большей наглядности рассеивание CB характеризуют стандартным или средним квадратичным отклонением (СКО)  , которое имеет такую же размерность, что и сама CB. Для более детального описания CB используют также асимметрию
, которое имеет такую же размерность, что и сама CB. Для более детального описания CB используют также асимметрию 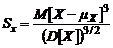 и эксцесс
и эксцесс 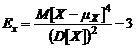 . Для симметричного относительно
. Для симметричного относительно 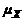 плотности распределения
плотности распределения  ,
,  , если распределение быстрее стремится к нулю слева от
, если распределение быстрее стремится к нулю слева от  – если справа. Эксцесс характеризует рассеивание CB около среднего значения по сравнению с нормальной CB, у которой Ex=0. Из определения M[X] и D[X] вытекают их следующие свойства:
– если справа. Эксцесс характеризует рассеивание CB около среднего значения по сравнению с нормальной CB, у которой Ex=0. Из определения M[X] и D[X] вытекают их следующие свойства: ;
; ;
;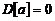 ;
;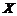 и
и 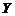 и неслучайных чисел
и неслучайных чисел 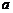 и
и 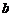
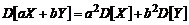 .
.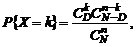 где N – объем партии, D – число дефектных единиц, n – объем выборки[1]. Среднее и дисперсия гипергеометрического распределения равны:
где N – объем партии, D – число дефектных единиц, n – объем выборки[1]. Среднее и дисперсия гипергеометрического распределения равны:

 <<1. Разлагая биноминальные коэффициенты через факториалы, получим
<<1. Разлагая биноминальные коэффициенты через факториалы, получим  .
. , будем иметь
, будем иметь  . Попарно сокращая факториалы числителя и знаменателя, преобразуем последнее выражение к виду
. Попарно сокращая факториалы числителя и знаменателя, преобразуем последнее выражение к виду .
. , где
, где  .
.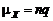 ;
;  .
. имеет конечный предел:
имеет конечный предел:  .
.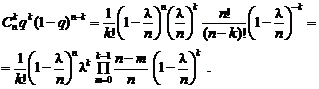
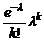 . Последний сомножитель при конечном k стремится к 1. Логарифмируя оставшийся сомножитель, получим
. Последний сомножитель при конечном k стремится к 1. Логарифмируя оставшийся сомножитель, получим .
. .
.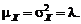
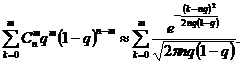
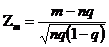 располагаются на числовой оси настолько тесно, что ряд в функции распределения можно заменить интегралом:
располагаются на числовой оси настолько тесно, что ряд в функции распределения можно заменить интегралом: где
где 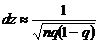 ,
,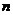 можно положить равным – ¥.
можно положить равным – ¥. называется плотностью распределения стандартной нормальной случайной величины.
называется плотностью распределения стандартной нормальной случайной величины. 
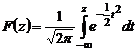 удобнее представить в виде
удобнее представить в виде 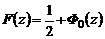 , где
, где 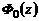 – функция Лапласа,
– функция Лапласа,
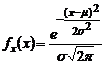 ;
;  ;
;