
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Преобразования случайных величинИ сущность метода Монте-Карло 1. Задача установления закона распределения и числовых характеристик функций от случайных величин представляет собой один из основных элементов статистического моделирования. Для простоты рассмотрим только случай функций c ограниченным количеством интервалов монотонности. Пусть СВ X и Y связаны между собой соотношением Y=X2 . В этом случае получим
Для обратного преобразования Y=
Эти соотношения используются при построении многих важных для практического применения композиционных законов распределения. В частности, если СВ X имеет стандартное нормальное распределение, то СВ Y=X 2 , имеющая плотность распределения представляет собой Пусть случайные величины Для показательного преобразования
Рассмотрим преобразование
2. Применим к непрерывной СВ Х собственную ФР, т.е. рассмотрим преобразование
где Продолжив преобразование, получим
Таким образом, автопреобразование  Генератор псевдослучайных чисел в серии повторных обращений выдает последовательную выборку из 3. Моделирование целочисленных случайных величин осуществляется путем разбиения единичного отрезка на интервалы, равные вероятностям их возможных значений. Пусть, например, требуется смоделировать (разыграть) полиномиальную СВ, у которой три возможных значения реализуются с вероятностями:
интерпретируем попадание равномерной на [0,1] СВ Y в каждый из интервалов как реализацию соответствующего исхода. Если дискретная СВ имеет N равновероятных значений, то моделирующим соотношением будет [NY]+1 , где [·] означает целую часть числа, заключенного в скобки. В качестве примера рассмотрим виртуальный лототрон, реализующий в пакете Mathcad-2001 последовательность независимых тиражей «Спортлото 6 из 49» (рис. 1.1.1). Более содержательные примеры приведены в приложении I.
Рис. 1.1.1. Текст программы-имитатора и таблица 10 тиражей
Системы случайных величин 1.На практике часто бывает необходимо определять вероятности совместной реализации нескольких СВ. Например, если известно, что двигатель автомобиля безотказно работает 100 тыс. км с вероятностью р1, а ходовая часть с вероятностью р2, то какова вероятность их совместной безотказной работы? Если эти два события независимы (обозначим их А и В), то вероятность совместного осуществления определяется формулой
Если события не являются независимыми, то вероятность их совместного появления определяется через условную вероятность:
Под условной вероятностью Установление независимости событий, либо определение условных вероятностей, часто делается из соображений по существу исследуемого процесса. Рассмотрим пример. В механизм входят две одинаковые шестерни. Технические условия нарушаются, если они обе окажутся с плюсовыми отклонениями по толщине зуба. У сборщика имеется 10 шестерен, из которых 3 «+» и 7 «-». Определим вероятность нарушения технических условий при сборке. Пусть событие А ~ {первая шестерня «+»}, событие В ~ {вторая шестерня «-»}. По правилу умножения находим Если же шестерни последовательно устанавливаются на двух рабочих местах и у двух сборщиков одинаковые партии шестерен, то А и В можно считать независимыми. В этом случае
Из соотношения (1.2.2) следует формула Байеса:
Пусть событие А по условиям опыта может осуществляться только совместно с каким-нибудь из событий полной группы (одной из гипотез) Безусловные вероятности
Апостериорные условные вероятности гипотез Р(Нk/A), то есть правдоподобие гипотез при условии, что событие А зафиксировано, определяются по формуле вероятностей правдоподобия гипотез Байеса:
Пусть в партии смешаны изделия от трех поставщиков в количестве n1,n2,n3. Известно, что вероятности дефектности для изделия 1-го, 2-го, 3-го поставщиков равны соответственно q1,q2,q3. Взятое наугад изделие оказалось дефектным. Требуется найти вероятность того, что оно принадлежит 1-му, 2-му и 3-му поставщикам. Пусть событие А ~{изделие оказалось дефектным}. Гипотезы, образующие полную группу, заключаются в следующем:
Из контекста задачи условные вероятности события А составляют: Апостериорные вероятности гипотез, вычисленные по формуле Байеса, после элементарных преобразований будут иметь вид
2. Пусть совокупность объемом N образуется по схеме Бернулли с вероятностью успеха p. Для наглядности представим, что корзина последовательно заполняется N шарами, которые независимо друг от друга могут быть черными с вероятностью p и белыми с вероятностью 1-р. Ряд распределения числа черных шаров, будет иметь вид
Из корзины извлекается безвозвратная выборка объемом n< N. Пусть Y число черных шаров в выборке. Ряд условного выборочного распределения согласно п.1.1 составит
Найдем ряд безусловного распределения Р{X = m}. Применяя формулу полной вероятности, получим
Комбинаторный множитель в последнем выражении после элементарных преобразований составит
Сумма в последнем выражении представляет собой полную сумму биноминального ряда В (p, N-n), стало быть равна 1. Таким образом доказана следующая теорема: Безвозвратная выборка из конечной биноминальной совокупности сохраняет биноминальный закон распределения с той же вероятностью успеха: 3. Рассмотрим другую ситуацию. Пусть имеется двухзвенная технологическая цепь с вероятностями успешного завершения операций p1 и p2 соответственно. Положим, что результаты последовательного прохождения компонентов полуфабриката (заготовок) независимы в совокупности, т.е. реализуется схема Бернулли. Пусть n – число заготовок, поступивших на вход первого звена. Тогда Y1 – число бездефектных полуфабрикатов на выходе первого звена будет подчиняться биноминальному закону P{Y1=m1}~B(p1,n). Выход первого звена является входом второго, и условное распределение P{Y2=m2 | Y1=m1}, m1 ≥ m2, также будет биноминальным: B(p2 ,m1). Безусловное распределение P{Y2 =m} согласно формуле полной вероятности составит:
Объединяя комбинаторные множители и перегруппировывая факториальные сомножители, получаем тождество
Далее, вынося из под знака суммы множители, не зависящие от m1, искомые вероятности получим в виде
Совершив замену индекса Возвращая (1.2.8) в (1.2.7), окончательно получаем следующее тождество:
что является доказательством следующей теоремы: Число успехов при испытаниях по двухзвенной схеме Бернулли подчиняется биноминальному закону с вероятностью успеха, равной произведению вероятностей успеха составляющих звеньев: B{p1,n}
Из этой теоремы вытекает доказываемое с помощью элементарной индукции следствие: для любого числа последовательных звеньев схемы Бернулли число успехов на выходе подчиняется биноминальному закону с вероятностью успеха, равной произведению вероятностей составляющих звеньев. 4. При совместном рассмотрении нескольких СВ следует различать два принципиально различных типа взаимодействия. Пусть имеется партия подшипниковых шариков, состоящая из продукции двух различных автоматов. Фактический диаметр шариков первого автомата имеет нормальное распределение с параметрами
Если при этом
Такой тип взаимодействия, представляющий собой сложение независимых СВ, называется композицией. При этом, если резисторы с двух линий смешиваются в общем накопителе в пропорции В данном случае имеет место совместное проявление суперпозиции и композиции двух СВ. Из этого простого примера ясно, что для результативности и эффективности любого статистического анализа необходимо детальное предметное рассмотрение схемы возникновения и взаимодействия СВ, что на практике нередко упускается из виду. 5. В приложениях математической статистики часто встречается задача установления закона распределения функции нескольких СВ. Сумма двух СВ Y=X1+X2 является частным случаем функции двух СВ. Исчерпывающей характеристикой пары СВ является функция их совместного распределения, которая определяется как вероятность совместности выполнения двух неравенств:
Функция распределения (1.2.12) обладает свойствами, аналогичными свойствам функции распределения одной СВ. Однако знание функций распределения F1(x1) и F2(x2) недостаточно для описания совместного распределения X1 и Х2, так как между ними возможно наличие стохастической зависимости — связи. При условии независимости X1 и Х2, что эквивалентно независимости событий A1@{X1<х1} и А2@{Х2<х2}, функция совместного распределения факторизуется и для ее определения достаточно знать функции распределения компонент F(x1,x2)=F(x1)F(x2). (1.2.13) Точно так же факторизуется и плотность совместного распределения:
Функция распределения СВ Y=X1+X2 представляет собой интеграл где D(y) - область плоскости х1оx2, определяемая из условия х1+х2<у (рис. 1.2.1). Рис. 1.2.1. Область интегрирования для определения ПР суммы двух СВ
Дифференцируя (1.2.15) по у, находим плотность распределения суммы:
или, учитывая симметрию функции Y=X1+Х2,
Интеграл (1.2.16) и эквивалентный ему (1.2.17) называется сверткой и обозначается символом g=f1*f2. (1.2.18) При композиции двух дискретных СВ интегралы (1.2.16) и (1.2.17) преобразуются в суммы:
В примере, приведенном в предыдущем пункте, был использован тот факт, что сумма двух нормальных величин также является нормальной, среднее значение и дисперсия которой равны соответственно сумме средних и сумме дисперсий слагаемых: m=m1+m2 , Для иллюстрации центральной предельной теоремы рассмотрим сумму независимых СВ с равномерным распределением на отрезке
Графики функций
Рис. 1.2.2. Нормализация суммы случайных слагаемых R(0,1)
Как видно, последовательность
6. В п. 1.1 была найдена плотность распределения квадрата стандартной нормальной СВ. Используя соотношение (1.2.16), найдем плотность распределения суммы квадратов двух независимых стандартных нормальных СВ:
При произвольном k>2, разделяя образующуюся последовательность по четным/нечетным номерам, ПР
где
Для целого аргумента Распределение
В приложениях часто встречаются распределения, получающиеся из При k=2 возникает распределение Рэлея – распределение эксцентриситета параллельных осей вала и отверстия: При k=3 возникает распределение Максвелла – распределение величины скорости молекулы газа в трехмерном пространстве: Среднее и дисперсия величины
7.Пусть СВ
Рис.1.2.3. Область интегрирования для определения произведения двух СВ
Интегрируя ПР совместного распределения по области
Дифференцируя по
Если
Если же 8.Для преобразования рис. 1.2.4.
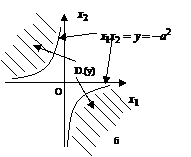
Рис.1.2.4. Область интегрирования для определения отношения двух СВ
Интегрируя, получаем ФР
Дифференцируем по
Для пары независимых и положительных СВ (1.2.30) преобразуется к виду
Пусть, Для отношения средних квадратов с Соотношение (1.2.33) есть ПР диперсионного отношения Фишера – основной инструмент дисперсионного анализа. 8.Найдем дисперсию суммы двух СВ, полагая наличие связи между ними. Используя свойства средних и дисперсий, получим
С помощью тождественного преобразования вида
где
Подставив (1.2.34) в (1.2.35), для дисперсии суммы будем иметь
Коэффициент корреляции, очевидно, сохраняет постоянное значение при масштабировании Множественная ковариация системы СВ
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
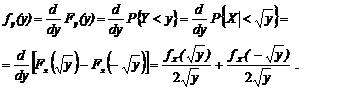 (1.1.1)
(1.1.1)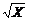 будем иметь
будем иметь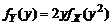 . (1.1.2)
. (1.1.2)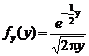 , (1.1.3)
, (1.1.3)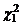 (Хи-квадрат) с одной степенью свободы и широко применяется в математической статистике. Среднее и дисперсия СВ с плотностью (1.1.3) равны: M[Y]=1; D[Y]=2.
(Хи-квадрат) с одной степенью свободы и широко применяется в математической статистике. Среднее и дисперсия СВ с плотностью (1.1.3) равны: M[Y]=1; D[Y]=2. 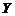 и
и 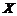 связаны соотношением
связаны соотношением 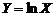 . Найдем ПР
. Найдем ПР 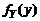 :
: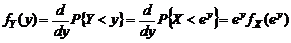 . (1.1.4)
. (1.1.4)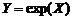 , обращая (1.1.4), получим
, обращая (1.1.4), получим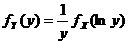 . (1.1.5)
. (1.1.5)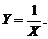 Для ПР
Для ПР 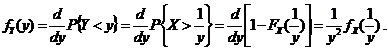 (1.1.6)
(1.1.6)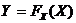 . В силу первого свойства ФР величина Y будет сосредоточена на отрезке [0,1]. Для ПР fY(y) полу чим
. В силу первого свойства ФР величина Y будет сосредоточена на отрезке [0,1]. Для ПР fY(y) полу чим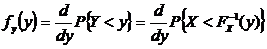 ,
,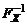 – функция, обратная к ФР
– функция, обратная к ФР 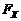 .
.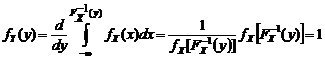 . (1.1.7)
. (1.1.7)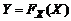 переводит любую непрерывную СВ в
переводит любую непрерывную СВ в 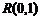 . Отсюда с очевидностью вытекает и обратное утверждение: преобразование
. Отсюда с очевидностью вытекает и обратное утверждение: преобразование 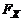 . Полученное тождество используется при статистическом моделировании случайных процессов методом «Монте-Карло».
. Полученное тождество используется при статистическом моделировании случайных процессов методом «Монте-Карло».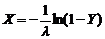 дает СВ с показательным распределением
дает СВ с показательным распределением 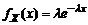 ,
, 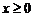 . Все типовые ПР реализованы в качестве стандартных функций в [6].
. Все типовые ПР реализованы в качестве стандартных функций в [6].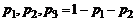 . Разбивая единичный отрезок на три интервала:
. Разбивая единичный отрезок на три интервала: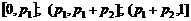 ,
,
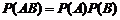 . (1.2.1)
. (1.2.1)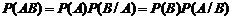 . (1.2.2)
. (1.2.2)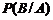 понимается вероятность наступления события
понимается вероятность наступления события 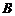 при условии, что событие
при условии, что событие 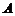 произошло. Для независимых событий
произошло. Для независимых событий 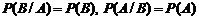 .
. 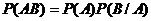 . Непосредственным подсчетом находим
. Непосредственным подсчетом находим 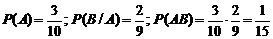 .
.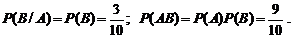

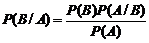 . (1.2.3)
. (1.2.3)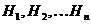 , удовлетворяющих условиям
, удовлетворяющих условиям 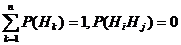 при
при 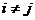 .
.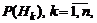 и априорные условные вероятности
и априорные условные вероятности 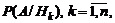 предполагаются известными. Тогда вероятность события А определяется формулой полной вероятности:
предполагаются известными. Тогда вероятность события А определяется формулой полной вероятности: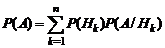 . (1.2.4)
. (1.2.4)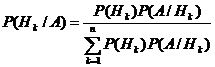 . (1.2.5)
. (1.2.5)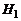 ~{изделие 1-го поставщика};
~{изделие 1-го поставщика}; 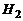 ~{изделие 2-го поставщика};
~{изделие 2-го поставщика}; 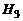 ~{изделие 3-го поставщика}. Их вероятности равны:
~{изделие 3-го поставщика}. Их вероятности равны: 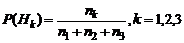 .
.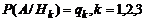 .
.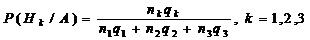 .
.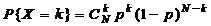 .
.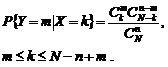 (1.2.6)
(1.2.6)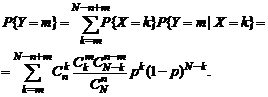
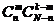 . Продолжив преобразования, получим
. Продолжив преобразования, получим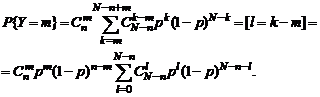
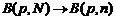 .
.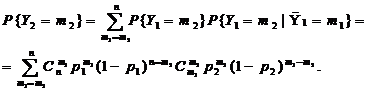
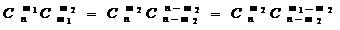 .
.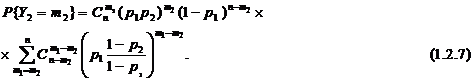
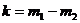 , сумму в последнем выражении преобразуем к виду
, сумму в последнем выражении преобразуем к виду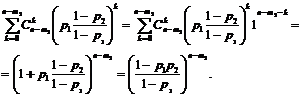 (1.2.8)
(1.2.8)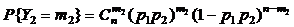 ,
,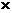 B{p2,n p1}→ B{p1p2,n).
B{p2,n p1}→ B{p1p2,n). , второго -
, второго - 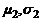 . Доли шариков первого и второго сорта равны соответственно
. Доли шариков первого и второго сорта равны соответственно 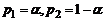 . Плотность распределения диаметра шариков в репрезентативной выборке из такой партии по формуле полной вероятности будет равна:
. Плотность распределения диаметра шариков в репрезентативной выборке из такой партии по формуле полной вероятности будет равна: . (1.2.9)
. (1.2.9)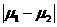 >
> 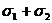 , то кривая плотности распределения будет иметь двухмодальный (двухгорбый) вид. Такой тип взаимодействия, когда с вероятностью
, то кривая плотности распределения будет иметь двухмодальный (двухгорбый) вид. Такой тип взаимодействия, когда с вероятностью 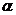 появляется СВ X1, a с вероятностью
появляется СВ X1, a с вероятностью 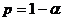 -СВ Х2, называется суперпозицией законов распределения. Если же продукцией автоматов являются, скажем, электрические сопротивления, которые затем соединяются в последовательную цепь, то номинальное сопротивление составных резисторов будет иметь ПР
-СВ Х2, называется суперпозицией законов распределения. Если же продукцией автоматов являются, скажем, электрические сопротивления, которые затем соединяются в последовательную цепь, то номинальное сопротивление составных резисторов будет иметь ПР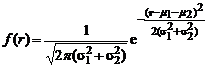 . (1.2.10)
. (1.2.10)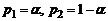 , а затем соединяются в цепь, то номинал составных резисторов будет иметь трехмодальное распределение с плотностью
, а затем соединяются в цепь, то номинал составных резисторов будет иметь трехмодальное распределение с плотностью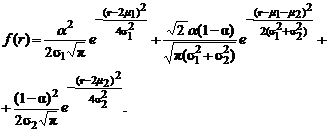 (1.2.11)
(1.2.11)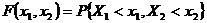 . (1.2.12)
. (1.2.12)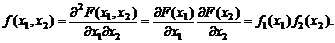 (1.2.14)
(1.2.14)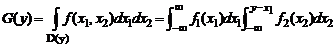 , (1.2.15)
, (1.2.15)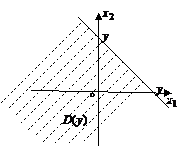
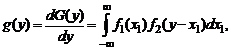 (1.2.16)
(1.2.16)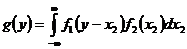 . (1.2.17)
. (1.2.17)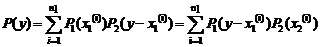 . (1.2.19)
. (1.2.19)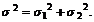 То же самое справедливо для любого числа независимых нормальных СВ. При этом плотность распределения суммы из n слагаемых будет представлять собой результат n-кратной последовательной свертки. Суммы непрерывных СВ с распределением, отличным от нормального, уже не сохраняют закон распределения слагаемых, даже если слагаемые распределены одинаково. Однако с увеличением числа слагаемых сумма всякий раз достаточно быстро нормализуется, что напрямую следует из центральной предельной теоремы.
То же самое справедливо для любого числа независимых нормальных СВ. При этом плотность распределения суммы из n слагаемых будет представлять собой результат n-кратной последовательной свертки. Суммы непрерывных СВ с распределением, отличным от нормального, уже не сохраняют закон распределения слагаемых, даже если слагаемые распределены одинаково. Однако с увеличением числа слагаемых сумма всякий раз достаточно быстро нормализуется, что напрямую следует из центральной предельной теоремы.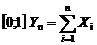 . Последовательно производя преобразования (1.2.16), получим для ПР
. Последовательно производя преобразования (1.2.16), получим для ПР 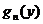 следующие рекуррентные соотношения:
следующие рекуррентные соотношения: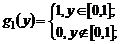 (1.2.20)
(1.2.20)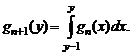 (1.2.21)
(1.2.21)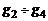 изображены на рис. 1.2.2.
изображены на рис. 1.2.2.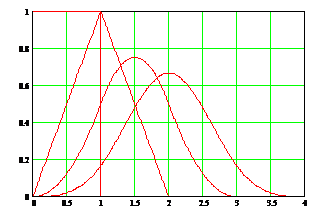
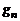 достаточно быстро приближается к кривой плотности нормального распределения с параметрами
достаточно быстро приближается к кривой плотности нормального распределения с параметрами 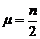 ,
, 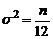 . Если ввести нормированную величину
. Если ввести нормированную величину 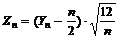 , то при n
, то при n 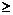 6 получим кривую, практически не- отличимую от стандартной нормальной кривой Гаусса:
6 получим кривую, практически не- отличимую от стандартной нормальной кривой Гаусса: 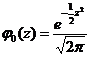 .
.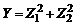 :
: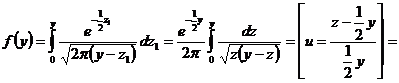
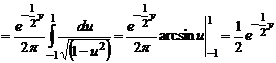 . (1.2.22)
. (1.2.22)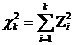 по индукции получаем в виде
по индукции получаем в виде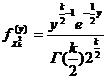 , (1.2.23)
, (1.2.23)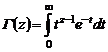 – гамма-функция Эйлера, обладающая следующими свойствами:
– гамма-функция Эйлера, обладающая следующими свойствами: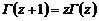 ,
, 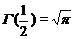 , Г (1)=1.
, Г (1)=1.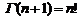
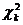 играет очень важную роль при решении многих прикладных задач математической статистики. Среднее и дисперсия
играет очень важную роль при решении многих прикладных задач математической статистики. Среднее и дисперсия 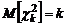 ;
; 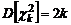 . (1.2.24)
. (1.2.24)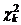 путем его преобразования. Например,
путем его преобразования. Например, 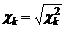 . Плотность распределения
. Плотность распределения 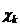 найдем, используя полученное в п. 1.1 соотношение (1.1.2):
найдем, используя полученное в п. 1.1 соотношение (1.1.2):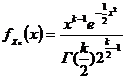 . (1.2.25)
. (1.2.25)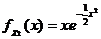 .
.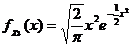 .
. 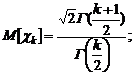
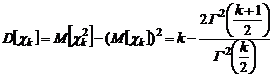 .
.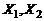 имеют ПР совместного распределения
имеют ПР совместного распределения 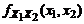 , а
, а 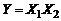 - их произведение. Область
- их произведение. Область 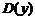 , удовлетворяющая условию
, удовлетворяющая условию 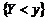 , показана на рис.1.2.3.
, показана на рис.1.2.3.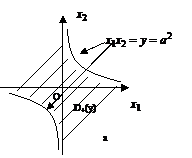
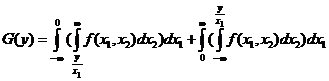 . (1.2.26)
. (1.2.26)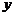 , находим ПР произведения:
, находим ПР произведения: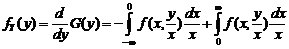 . (1.2.27)
. (1.2.27)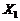 и
и 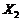 независимы и симметричны относительно нуля, то (1.2.27) преобразуется к виду
независимы и симметричны относительно нуля, то (1.2.27) преобразуется к виду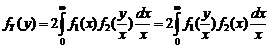 . (1.2.28)
. (1.2.28)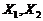 независимые положительно–определенные СВ, то множитель 2 исчезает.
независимые положительно–определенные СВ, то множитель 2 исчезает.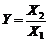 область
область 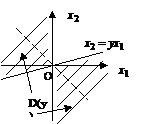
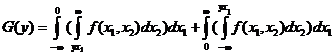 . (1.2.29)
. (1.2.29)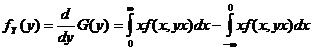 . (1.2.30)
. (1.2.30)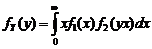 . (1.2.31)
. (1.2.31)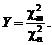 Подставляя в (1.2.31) ПР (1.2.23), получим
Подставляя в (1.2.31) ПР (1.2.23), получим 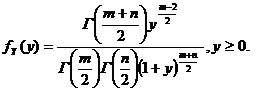 (1.2.32)
(1.2.32)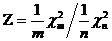 , связанного
, связанного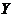 линейным соотношением
линейным соотношением 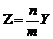 , будем иметь
, будем иметь 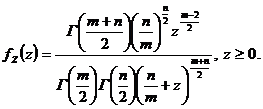 (1.2.33)
(1.2.33)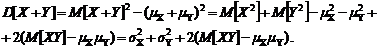 (1.2.34)
(1.2.34) получаем, что последнее слагаемое в (1.2.34) представляет собой смешанный второй центральный момент
получаем, что последнее слагаемое в (1.2.34) представляет собой смешанный второй центральный момент 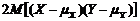 . Таким образом, окончательно дисперсию суммы получаем в виде
. Таким образом, окончательно дисперсию суммы получаем в виде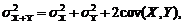 (1.2.35)
(1.2.35)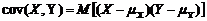 - ковариация, служащая мерой линейной зависимости между Х и Y. Удельная мера, или коэффициент корреляции, определяется как
- ковариация, служащая мерой линейной зависимости между Х и Y. Удельная мера, или коэффициент корреляции, определяется как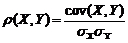 .
.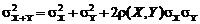 . (1.2.36)
. (1.2.36)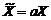 ,
, 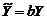 , где a и b – произвольные положительные константы. Полагая
, где a и b – произвольные положительные константы. Полагая 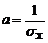 ,
, 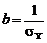 , получим
, получим 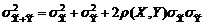 . Так как
. Так как 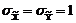 ,
, 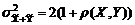 . Левая часть последнего соотношения неотрицательна, следовательно
. Левая часть последнего соотношения неотрицательна, следовательно 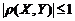 .
.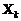 задается симметричной ковариационной матрицей n×n. На главной диагонали стоят дисперсии
задается симметричной ковариационной матрицей n×n. На главной диагонали стоят дисперсии 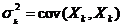 . Внедиагональные элементы представляют собой соответствующие ковариации
. Внедиагональные элементы представляют собой соответствующие ковариации 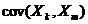 . Путем деления ковариационной матрицы на соответствующие дисперсии образуется корреляционная матрица, сохраняющая симметрию. На ее главной диагонали стоят 1, внедиагональными элементами являются коэффициенты корреляции
. Путем деления ковариационной матрицы на соответствующие дисперсии образуется корреляционная матрица, сохраняющая симметрию. На ее главной диагонали стоят 1, внедиагональными элементами являются коэффициенты корреляции 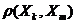 .
.