Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модели выбора оптимального набора контрольных мероприятий⇐ ПредыдущаяСтр 11 из 11 Теперь рассмотрим в качестве интегрального показателя при контроле – неопределенность в системе. Под неопределенностью понимается характеристика объема информации, имеющейся в распоряжении у субъекта об изучаемом объекте и окружающей среде, отражающая объективное наличие факторов случайной природы, а также неполноту и неточность информации и знаний об объекте, оказывающих существенное влияние на итоговый результат деятельности. Существуют различные источники и типы неопределенности. В зависимости от причины ее возникновения меняется и способы ее измерения. Говоря о неопределенности, нельзя не упомянуть о риске. Эти понятия хотя во многом и схожи, все-таки различаются. Риск – вероятность возникновения убытков или снижения доходов по сравнению с прогнозируемым вариантом. Понятие неопределенности более общее. Понятие же риска субъективно, оно выражает оценку возможности возникновения неблагоприятных для конкретного лица последствий принятия решения. Поэтому условия плохие для одного лица принимающего решения могут быть хорошими для другого. Для измерения неопределенности вводится функция меры неопределенности, обладающая следующими свойствами: 1. 2. 3. Если  Будем рассматривать социально-экономическую систему (СЭС), состоящую из центра и
Процесс накопления неопределенности в
В качестве функции меры неопределенности выберем линейную зависимость
Тогда цель в задаче может быть сформулирована как минимизация общей неопределенности в системе здесь Для формулирования ограничений задачи введем следующие переменные: Получаем следующее ограничение на ресурсы Пусть, кроме того, В этом случае задача (1)-(2) простейшая задача оптимизации и для нее может быть найдено аналитическое решение. Отметим далее, что поскольку
Учитывая замену
Легко показать, что решением задачи (4),(5) является
Чтобы решать задачу (4)-(5) необходимо, чтобы были заданы параметры Кроме того, представляется целесообразным введение ограничений на использование не только временных ресурсов при управлении подсистемами. В общем случае задача имеет вид
здесь Ограничения модели имеют следующий смысл (8) – ограничение на ресурсы, необходимые для проведения управленческих мероприятий, кроме временных ресурсов, учитываемых в (7). Ограничение (9) регулирует периодичность проведения мероприятий в подсистемах. Основным недостатком рассмотренной модели является сложность расчета параметров. Можно предложить следующий способ поиска величины скорости накопления неопределенности. Будем полагать, что для каждой отдельной подсистемы может быть найден некоторый главный параметр характеристик – агрегированный показатель, тогда скорость накопления неопределенности – изменчивость, волатильность основного показателя функционирования подсистемы. Модель отыскания числа контрольных мероприятий, минимизирующих неопределенность. Иногда удобнее неопределенность вводить как функцию от числа контрольных мероприятий. Рассмотрим процесс обучения, который необходимо контролировать. Есть некоторый административный центр и K групп.
Предлагаются 2 подхода к поиску величины 1. Если известны данные об оценках обучаемых за некоторый период [1,2,..,
Т.о. накопление неопределенности происходит из-за изменения оценок группы в процессе обучения, т.е. чем больше колебания в процессе обучения, тем неопределеннее итоговый результат. Второй подход основан на предположении, что неопределенность в оценке качества обучения возникает, когда итоговая оценка каждого обучаемого отличается от оценки, прогнозируемой по промежуточным результатам. Пусть
Ограничениямодели имеют вид
Модель поиска набора управленческих мероприятий, с энтропией в качестве функции цели. В данной модели предлагается искать не только набор управляющих мероприятий, но и моменты их проведения, т.е. учтена возможность неравномерности проведения мероприятий. Пусть необходимо организовать контроль в образовательном учреждении (ОУ) в период времени Величина неопределенность, связанная с проведением Т.о. получаем следующую модель
Полученная задача с линейными ограничениями и нелинейной функцией цели, относится к типу распределительных задач. Задачи 1.Головной офис планирует контроль за 7 филиалами, расположенными в различных городах. Анализ их работы и различий (удаленность, размер филиала, возраст и т.д.) позволил экспертам компании оценить характеристики, необходимые для расчета периодичности проведения контрольных мероприятий по модели равномерного контроля
2.Обучение двух групп контролировалась с помощью проведения 5 промежуточных и одного итогового тестов, оцениваемых в 100 балльной системе.
Определите возможность прогнозирования результатов обучения групп на основе оценки скорости накопления неопределенности в группах. Литература Основная литература 1. Анфилатов В.С. Системный анализ в управлении : учеб. пособие для вузов по специальности "Прикладная информатика" / В.С. Анфилатов, А.А. Емельянов, А.А. Кукушкин. — М. : Финансы и статистика, 2003. — 367 с. 2. Острейковский В.А. Теория систем : учеб. для студ. вузов / В.А. Острейковский. — М. : Высш. шк., 1997. — 239 с. 3. Клир Дж. Системология. Автоматизация решения системных задач / Дж. Клир. — М. : Радио и связь, 1990. — 538 с. Дополнительная литература 1. Дрогобыцкий И.Н. Системный анализ в экономике / И.Н. Дрогобыцкий. – М. : Финансы и статистика, 2007. – 512 с. 2. Миротин Л.Б. Системный анализ в логистике : учеб. для студ. вузов / Л.Б. Миротин, Ы.Э. Ташбаев. — М. : Экзамен, 2004. — 479 с. 3. Фрейдина Е.В. Исследование систем управления : учеб. пособие / Е.В. Фрейдина. – М. : Омега-Л, 2008. – 367 с. 4. Бабунашвили М.К. Контроль и управление в организационных системах / М.К. Бабунашвили, М.А. Бермант, И.Б. Руссман // Экономика и математические методы. – 1969. – Т. 5, № 2. – С. 212-227. 5. Руссман И.Б. О проблеме оценки качества / И.Б. Руссман, М.А. Бермант // Экономика и математические методы. – 1978. – Т. 24, № 4. – С. 202-213.
Учебное издание ОСНОВЫ ТЕОРИИ СИСТЕМ И ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ СИСТЕМНОГО АНАЛИЗА
Методическое пособие для вузов
Составители: Н.Б. Баева, Д.В. Ворогушина Е.В. Куркин
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 286. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
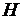 - непрерывная функция своего аргумента в области определения. Более сильное требование непрерывной дифференцируемости
- непрерывная функция своего аргумента в области определения. Более сильное требование непрерывной дифференцируемости 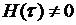
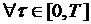 . Поскольку исследуемый объект непознаваем до конца, то даже в начальный момент или когда
. Поскольку исследуемый объект непознаваем до конца, то даже в начальный момент или когда 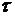 достаточно мало,
достаточно мало, 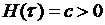 , где
, где 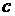 величина неустранимой неопределенности.
величина неустранимой неопределенности.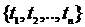 - точки, характеризующие моменты времени, когда проводятся контрольные мероприятия, то очевидным представляется, что число этих точек находится в обратной зависимости от величины
- точки, характеризующие моменты времени, когда проводятся контрольные мероприятия, то очевидным представляется, что число этих точек находится в обратной зависимости от величины 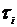 .
.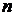 относительно независимых друг от друга, управляемых подсистем, в период времени [0,
относительно независимых друг от друга, управляемых подсистем, в период времени [0, 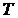 ]. Пусть
]. Пусть 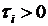 - временной период между соседними точками проведения управляющих мероприятий в
- временной период между соседними точками проведения управляющих мероприятий в 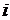 -той подсистеме,
-той подсистеме, 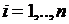 . Функцию меры неопределенности в системе введем как аддитивную монотонную функцию мер неопределенности каждой подсистемы
. Функцию меры неопределенности в системе введем как аддитивную монотонную функцию мер неопределенности каждой подсистемы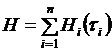
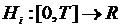
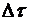 и не зависит от выбора начальной точки на временной оси
и не зависит от выбора начальной точки на временной оси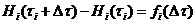 .
.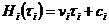
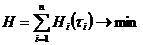 (1)
(1) 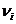 - некоторая константа, характеризующая скорость накопления неопределенности;
- некоторая константа, характеризующая скорость накопления неопределенности; 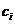 - величина неустранимой неопределенности в
- величина неустранимой неопределенности в 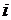 -той подсистеме. Поиск характеристики скорости накопления неопределенности осуществляется на основе истории управления подсистемами и должен зависеть от степени «управляемости» каждой подсистемы, т.е. реакции на управляющие воздействия центра. Будем считать, что известны скорости накопления неопределенности для всех подсистем
-той подсистеме. Поиск характеристики скорости накопления неопределенности осуществляется на основе истории управления подсистемами и должен зависеть от степени «управляемости» каждой подсистемы, т.е. реакции на управляющие воздействия центра. Будем считать, что известны скорости накопления неопределенности для всех подсистем 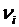
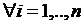 .
.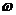 - доля периода
- доля периода 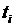 - промежуток времени, за который центр обрабатывает один опрос
- промежуток времени, за который центр обрабатывает один опрос 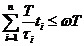 (2)
(2)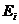 - полное количество информации, которое может получить центр от
- полное количество информации, которое может получить центр от 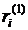 - стоимость единицы полезной информации, полученной от
- стоимость единицы полезной информации, полученной от 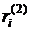 .
. 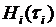 - оценка неопределенности подсистем, то
- оценка неопределенности подсистем, то 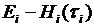 - количество полезной информации от
- количество полезной информации от  (3)
(3)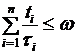 (4)
(4)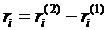 , получаем
, получаем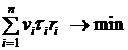 (5).
(5).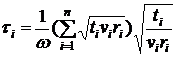 ,
,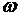 ,
, 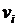 ,
, 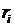 для каждой подсистемы.
для каждой подсистемы.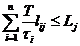
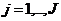 (8)
(8)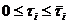
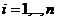 (9)
(9)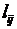 - величина
- величина 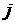 -того ресурса (за исключением временного), необходимого для проведения одного управленческого мероприятия в
-того ресурса (за исключением временного), необходимого для проведения одного управленческого мероприятия в 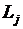 - общее наличие
- общее наличие 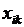 -число контрольных мероприятий
-число контрольных мероприятий 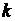 -той группе. Тогда неопределенность состояния всей системы имеет вид
-той группе. Тогда неопределенность состояния всей системы имеет вид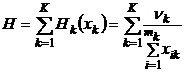
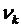 :
: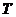 ], то величину
], то величину 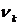 предлагается искать по формуле
предлагается искать по формуле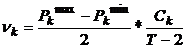 ,
,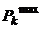 ,
, 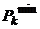 - соответственно максимальная и минимальная средние оценки
- соответственно максимальная и минимальная средние оценки 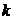 -той группы, полученные за период
-той группы, полученные за период 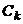 - число смены тенденций изменения средней оценки в
- число смены тенденций изменения средней оценки в 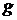 -номер обучаемого. Для реализации данного подхода, необходима информация об итоговой оценке каждого обучаемого за период [1,2,..,
-номер обучаемого. Для реализации данного подхода, необходима информация об итоговой оценке каждого обучаемого за период [1,2,.., 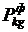 . Кроме того, по промежуточным результатам обучения рассчитывается прогнозируемая итоговая оценка
. Кроме того, по промежуточным результатам обучения рассчитывается прогнозируемая итоговая оценка 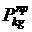 , например, с помощью методов прогнозирования предложенных в пакете Statistica 6.0. Величину
, например, с помощью методов прогнозирования предложенных в пакете Statistica 6.0. Величину 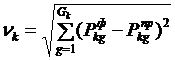
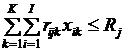 ,
, 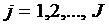 ;
; 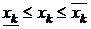 ,
, 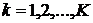 ;
; 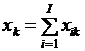 ,
, 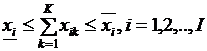
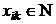 ,
, 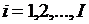 ,
,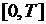 . При этом общее число занятий согласно учебному плану
. При этом общее число занятий согласно учебному плану 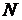 , Разделим период
, Разделим период 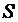 отрезков,
отрезков,  ,
, 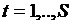 . Обозначим
. Обозначим 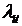 - число
- число 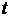 ;
;  -общее число
-общее число  . Тогда
. Тогда 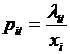 - доля
- доля 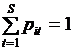 .
.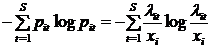 (10 )
(10 )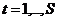 , причем оно не зависит от проведения такого же рода мероприятий в другие моменты времени.
, причем оно не зависит от проведения такого же рода мероприятий в другие моменты времени.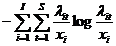
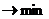
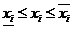 ,
, 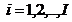
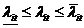 ,
, 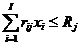 ,
, 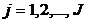
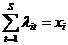 ,
, 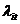 ,
, 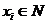
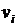 При этом аналитический отдел готов тратить на анализ состояния в филиалах и контроль не более 25% рабочего времени. Найдите периодичность проведения контрольных мероприятий в каждом филиале. В каких единицах будет измеряться ответ? Какой смысл в данной постановке задачи может иметь скорость накопления неопределенности ?
При этом аналитический отдел готов тратить на анализ состояния в филиалах и контроль не более 25% рабочего времени. Найдите периодичность проведения контрольных мероприятий в каждом филиале. В каких единицах будет измеряться ответ? Какой смысл в данной постановке задачи может иметь скорость накопления неопределенности ?