
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка качества объекта на основе коэффициентов «трудности»Подход к измерению характеристик качества на основе коэффициентов трудности был предложен М.К. Бабунашвили, М.А. Бермантом, И.Б. Руссманом, которые при определении влияния качества ресурсов на качество результата функционирования системы выяснили, что оценивание результата существенно зависит от предъявляемых к нему требований. Введем обозначения, которые в дальнейшем будем использовать:
Понятие трудности возникло из соображений о том, что получить результат определенного качества тем труднее, чем ниже качество ресурса или чем выше требования к качеству результата (при прочих равных условиях). Трудность выступает как обобщенная характеристика качества (некачественности) ресурса, учитывающая не только его свойства, но и требования, предъявляемые к нему системой. Предположим, что мы располагаем объектом, который может быть охарактеризован двумя свойствам, или комплексным ресурсом, состоящим из двух компонент. Положим также, что их качественные оценки имеют значения  Сформулируем некоторые свойства, которым должна удовлетворять 1. 2. 3. 4. Теорема. Единственной целой аналитической функцией от двух переменных В дальнейшем удобно оперировать с трудностью как с обобщенной характеристикой качества, получая из неё в случае необходимости значения Для случая
Рассмотрим теперь форму зависимости парциальной трудности Очевидно, а) б) величина в) Этим трем условиям удовлетворяет функция вида
Полагаем также, что Исследования полученной зависимости на основании вероятностной трактовки величин Итак, парциальная трудность Рассмотрим далее вопрос о получении обобщенных оценок качества комплексного ресурса системы и требований к нему. Для этого введем арифметические операции над трудностями: Таблица. Обобщенные операции
Введенные обобщенные операции образуют алгебраическую систему на множестве [0,1] с единичным элементом На основе данных операций, по аналогии с производственными функциями, можно ввести квалитативные функции Данная функция построенная с помощью обобщенных операций будет удовлетворять следующим условиям: 1) если парциальная трудность по какой-либо
2) если парциальная трудность по какой-либо компоненте равна нулю, то мера несоответствия не зависит от трудности по этой компоненте; По аналогии с производственными функциями можно ввести следующие виды квалитативных функций: 1) с нулевой эластичностью замены здесь коэффициенты 2) линейная функция 3) функция Кобба-Дугласа 4) функция CES (c постоянной эластичностью замены)
Параметры квалитативных функций могут быть найдены, например, нелинейным методом наименьших квадратов на основе предыстории функционирования рассматриваемой системы. Таким образом, для определения качества получаемого продукта можно использовать квалитативные функции. Для одновременного учета как количественной, так и качественной характеристик выпускаемой продукции предлагается использовать производственно-квалитативные функции. Пример 1. Рассматривается производство продукта с использованием двух ресурсов (
Рассчитаем минимальные требования к качеству ресурсов и текущее значение качества ресурса.
Тогда величина трудности Таким образом, качество второго ресурса не влияет на качество выпускаемого продукта, поскольку к нему не предъявляются требования (
Т.е. ожидаемое качество продукта - 0,67. Для повышения качества необходимо увеличить качество ресурсов ( Пример 2. Распишем квалитативную функцию Кобба-Дугласа через стандартные арифметические операции
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 365. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
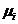 - качество
- качество 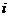 -й компоненты комплексного ресурса,
-й компоненты комплексного ресурса, 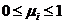 ;
;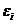 -требование к качеству
-требование к качеству 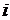 -й компоненты комплексного ресурса, индуцированное требованиями к качеству результата,
-й компоненты комплексного ресурса, индуцированное требованиями к качеству результата, 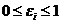 ,
, 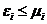 ,
, 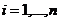 ;
;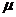 - интегральное качество комплексного ресурса,
- интегральное качество комплексного ресурса, 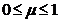 ;
;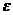 - требование к качеству комплексного ресурса,
- требование к качеству комплексного ресурса, 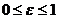 ,
, 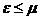 ;
;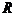 -результат, получение которого является целью функционирования организационной системы;
-результат, получение которого является целью функционирования организационной системы; 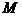 - качество результата,
- качество результата, 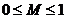 ;
;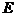 - требование к качеству результата,
- требование к качеству результата, 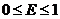 ,
, 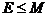 ;
;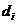 - парциальная трудность получения результата, удовлетворяющего требованию
- парциальная трудность получения результата, удовлетворяющего требованию 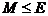 при условии, что качество
при условии, что качество 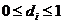 ;
;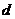 - общая трудность достижения результата,
- общая трудность достижения результата, 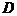 - мера несоответствия качества полученного результата предъявляемым к нему требованиям,
- мера несоответствия качества полученного результата предъявляемым к нему требованиям, 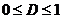 .
.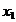 и
и 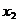 , причем
, причем 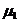 и
и 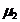 . В то же время они могут быть оценками качества, выраженными через трудности
. В то же время они могут быть оценками качества, выраженными через трудности 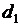 и
и 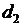 . Обобщенная оценка будет:
. Обобщенная оценка будет: 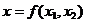 .
.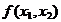 .
.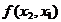 - свойство коммутативности оценок;
- свойство коммутативности оценок;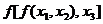 =
= 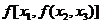 - свойство ассоциативности;
- свойство ассоциативности;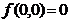 ,
, 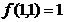 ,
, 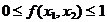 ,
, 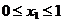 ,
, 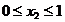 - если каждое из свойств объекта имеет нулевую или единичную оценку, то и обобщенная оценка будет соответственно равна нулю или единице. При этом все значения обобщенной оценки лежат в интервале
- если каждое из свойств объекта имеет нулевую или единичную оценку, то и обобщенная оценка будет соответственно равна нулю или единице. При этом все значения обобщенной оценки лежат в интервале 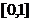 ;
;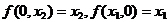 .
.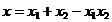
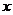 понимается трудность
понимается трудность 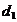 и
и 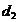 , то
, то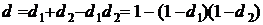 ,
, 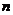 компонент комплексного ресурса имеем
компонент комплексного ресурса имеем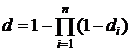 .
. 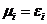 должна быть максимальной, т.е. равной единице. Действительно, трудность получения результата максимальна при предельно низком допустимом значении качества;
должна быть максимальной, т.е. равной единице. Действительно, трудность получения результата максимальна при предельно низком допустимом значении качества;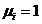 и
и 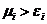 должна быть минимальной, т.е. равной нулю. Действительно, при предельно высоком возможном значении качества независимо от требований (при
должна быть минимальной, т.е. равной нулю. Действительно, при предельно высоком возможном значении качества независимо от требований (при 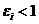 ) трудность должна быть минимальной;
) трудность должна быть минимальной;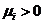 и
и 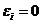 должна быть минимальной, т.е. равной нулю. Это очевидно, т.к. если к качеству компоненты ресурса не предъявляется никаких требований, а
должна быть минимальной, т.е. равной нулю. Это очевидно, т.к. если к качеству компоненты ресурса не предъявляется никаких требований, а 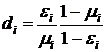 при
при 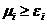 .
. 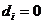 при
при 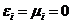 и
и 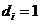 при
при 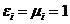 .
.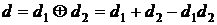
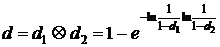
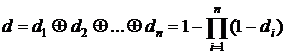
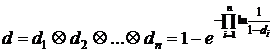
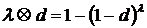
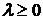 )
)
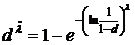
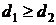 )
)
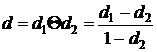
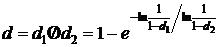
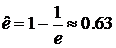 .
.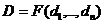 , показывающие меру несоответствия качества полученного результата предъявляемым к нему требованиям.
, показывающие меру несоответствия качества полученного результата предъявляемым к нему требованиям. 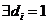 влечет
влечет 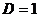 ;
;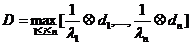
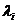 аналогичны коэффициентам фондоемкости.
аналогичны коэффициентам фондоемкости.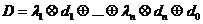 , .
, . 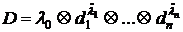 .
. 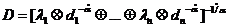 .
.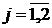 ). Известны количественные характеристики ресурсов (
). Известны количественные характеристики ресурсов ( 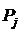 ) и возможные границы их изменения (
) и возможные границы их изменения ( 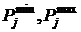 ), влияющие на качество ресурса. Необходимо рассчитать качество, выпускаемого продукта (
), влияющие на качество ресурса. Необходимо рассчитать качество, выпускаемого продукта ( 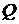 ) на основе понятия «трудности».
) на основе понятия «трудности».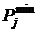
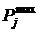
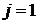
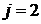
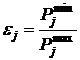 :
: 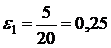 ,
, 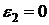 ,
,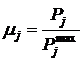 :
: 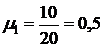 ,
, 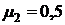 .
.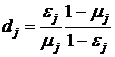 :
: 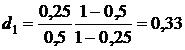 ,
, 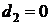 .
.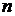 компонентам комплексного ресурса (
компонентам комплексного ресурса ( 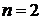 ), получаем
), получаем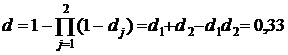 ,
, 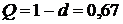 .
.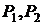 ) или снизить требования к качеству (
) или снизить требования к качеству ( 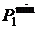 ) .
) .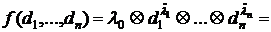
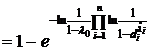
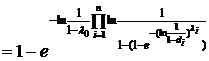
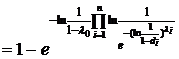
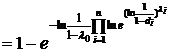
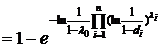 .
.