
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модель равномерного контроля на основе трудности достижения целиВводится величина «трудности достижения цели», как обобщенная характеристика качества
Полагаем также, что Пусть теперь
график, которой представляет S-образную кривую,
Простая подстановка приводят нас к формуле Общая трудность контроля в системе определяется следующим образом
и характеризует общий риск недостижения цели по всем подсистемам. Ограничения на использование ресурсов при проведении контроля в системе, состоящей из центра и

Пусть задан промежуток Пример 1. Рассмотрим задачу нахождения моментов контроля при известной теоретической траектории F(t) движения объекта к цели (область вокруг точки (Aпл, tпл)), известных из предыстории максимальной Vmax и минимальной Vmin скорости движения. В качестве функции цели рассмотрим минимизацию трудности достижения цели. Для решения данной задачи будем применять следующий алгоритм: 1. Определение F(t) траектории и параметров Aпл, tпл, Vmax, Vmin. 2. Нахождение точки контроля t0 дающей минимум трудности на основе решения задачи (1)-(6):
где (4)-(6) задает отрезок для поиска точки контроля, выражение (3) дает значение трудности характеризующее приближение к прямой СD. Как отмечалось выше из область ниже этой прямой двигаясь даже с максимальной скоростью нельзя достигнуть цели в срок, поэтому при приближении к CD выражение (3) растет. Аналогично значение выражения (2) увеличивается при приближении к прямой OD, поскольку область ниже прямой OD также будем считать запретной, хотя теоретически из этой области мы могли бы достичь цели в плановый срок, тем не менее, движение объекта со скоростью ниже минимальной говорит о нарушениях в функционировании объекта. Выражение (1) есть сложение двух трудностей. Отметим что в некоторых частных случаях (1) может иметь и другой вид. 3. «Свободное» функционирование объекта до момента t0. 4. Оценка состояния экономического объекта в момент времени t0: определение реального положения – величины достигнутого результата 5. Вычисление величины отклонения от запланированной траектории 6. Перерасчет параметров в задаче (1)-(6) согласно достигнутому результату 7. Целевой результат достигнут. При необходимости восстанавливаем реальную траекторию движения по контрольным точкам. Конец. Рассмотрим работу алгоритма на иллюстративном примере предприятия по производству кирпича. Пусть по данным из предыстории известны минимальная скоростью движения объекта 10,10 млн. штук кирпичей в месяц и максимальная – 36,61 млн. штук. Также имеется оптимальная с некоторой точки зрения траектория F(t) достижения планового результата Aпл=598,44, за расчетный период tпл=24 месяца. Допустимые отклонения от целевого результата в обе стороны
Графическое представление задачи Решая задачу (1)-(6) методом Соболя, получаем момент контроля t0=10 – это момент времени, в который необходимо будет произвести оценку состояния нашего объекта. Для поиска следующей точки контроля рассмотрим два возможных варианта, в которых может оказаться объект по прошествии времени t0: 1) Контрольные мероприятия показали, что объект не отклонился от запланированный траектории, тогда согласно алгоритму, необходимо просто с новыми параметрами Aпл, tпл по задаче (1)-(6) найти следующую точку контроля с использованием старой траектории F(t).
Расчет следующей точки контроля Следующей точкой контроля в нашем примере является t0=13. 2) Контрольные мероприятия показали, что величина отклонения от запланированной траектории развития является критической, поэтому согласно алгоритму необходимо произвести перерасчет теоретической траектории, учитывая положение в котором оказался исследуемый экономический объект. Без ограничения общности, можно считать, что мы оказались выше оптимальной траектории, и объём произведенной продукции составил 200 млн. штук вместо планируемых 131 млн.:
Перерасчёт траектории развития Строим новую траекторию развития Описанный процесс повторяется циклически, до тех пор, пока экономический объект не достигнет цели: не попадёт в целевой прямоугольник. Задачи 1.Решается вопрос о планировании числа контрольных мероприятий в школе для учеников 10-11 классов по предмету «Алгебра и начала анализа» с целью повышения вероятности успешной сдачи учениками ЕГЭ. На основе учебных планов и методических разработок выбраны 3 возможных программы контроля. Виды контрольных мероприятий и степень их влияния (значимости) на мотивацию учащихся приведены в таблице.
Укажите наиболее эффективный набор контрольных мероприятий на основе расчета величины общей трудности контроля: 2. Крупная компания планирует контроль финансового положения своих филиалов. В качестве методов выбраны: наблюдение (общее ознакомление с состоянием финансовой деятельности); проверка (затрагивает основные вопросы финансовой деятельности и проводится на месте с использованием различных документов); обследование (производится в отношении отдельных сторон финансовой деятельности и опирается на более широкий круг показателей, чем при проверке); анализ (проводится на базе текущей или годовой отчетности и отличается системным и пофакторным исследованием); ревизия (проводится на месте и основывается на проверке первичных документов, учетных регистров, бухгалтерской и статистической отчетности, фактического наличия денежных средств). Разработано 3 разных программы контроля за финансовой деятельностью филиалов в течении года. Придайте различным методам контроля веса значимости и на основе расчета величины общей трудности контроля, выберите оптимальную программу.
3. Составьте задачу о выборе числа контрольных мероприятий на транспорте, если известна длина маршрута, оценка числа пассажиров на каждой остановке и число контролеров. |
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 354. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , зависящая от качества работы подсистемы
, зависящая от качества работы подсистемы 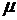 и от минимального требования к качеству
и от минимального требования к качеству 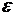 ,
,  . Напомним, что трудность рассчитывается следующим образом
. Напомним, что трудность рассчитывается следующим образом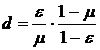 при
при 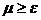 .
. 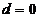 при
при 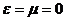 и
и 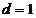 при
при 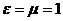 .
.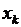 -число контрольных мероприятий в
-число контрольных мероприятий в 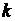 -той подсистеме,
-той подсистеме,  характеризует качество как функции от числа контрольных мероприятий в k-й подсистеме. Психофизиологические соображения и исследования приводят к логистической зависимости:
характеризует качество как функции от числа контрольных мероприятий в k-й подсистеме. Психофизиологические соображения и исследования приводят к логистической зависимости: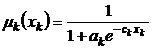 ,
,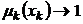 при
при  ,
, 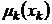 - монотонно возрастает от
- монотонно возрастает от 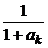 до 1 при возрастании
до 1 при возрастании 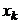 от нуля до бесконечности. Здесь
от нуля до бесконечности. Здесь 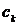 - характеризует важность каждого отдельного контрольного мероприятия, а коэффициент
- характеризует важность каждого отдельного контрольного мероприятия, а коэффициент 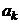 характеризует оценку значимости (вклада) каждого контрольного мероприятия по сравнению с предыдущим. Если нижнее допустимое (пороговое) значение качества обозначить
характеризует оценку значимости (вклада) каждого контрольного мероприятия по сравнению с предыдущим. Если нижнее допустимое (пороговое) значение качества обозначить  , то в нашем случае
, то в нашем случае 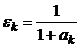 . Из этих двух характеристик сформируется оценка трудности достижения цели для
. Из этих двух характеристик сформируется оценка трудности достижения цели для 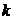 -той подсистемы:
-той подсистемы: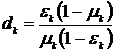 ,
, 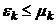 .
.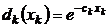 ,
, 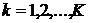 .
.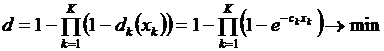
 групп имеют следующий вид
групп имеют следующий вид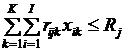 ,
, 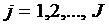 ;
; 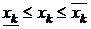 ,
, 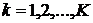 ;
; 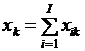 ,
, 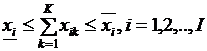
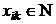 ,
, 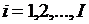 ,
,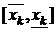 возможного изменения общего числа контрольных мероприятий в k-й группе. Пусть, кроме того, задан промежуток
возможного изменения общего числа контрольных мероприятий в k-й группе. Пусть, кроме того, задан промежуток 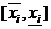 изменения допустимого числа контрольных мероприятий
изменения допустимого числа контрольных мероприятий 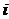 -того вида. Предположим, что
-того вида. Предположим, что 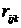 - затраты
- затраты 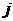 -го вида ресурса на реализацию одного контрольного мероприятия
-го вида ресурса на реализацию одного контрольного мероприятия 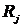 - объем имеющихся ресурсов j-го вида.
- объем имеющихся ресурсов j-го вида.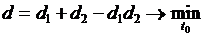 (1)
(1)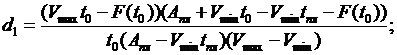 (2)
(2)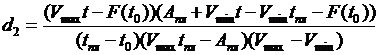 ; (3)
; (3) ; (4)
; (4)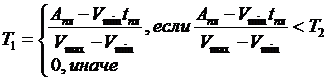 ; (5)
; (5)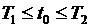 ; (6)
; (6)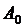 . Если объект попал в целевую область, то переход к шагу 7, иначе к шагу 5.
. Если объект попал в целевую область, то переход к шагу 7, иначе к шагу 5.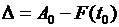 . Если величина отклонения критическая (например,
. Если величина отклонения критическая (например, 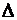 больше некоторого заданного
больше некоторого заданного 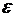 ), то необходимо произвести пересчёт траектории.
), то необходимо произвести пересчёт траектории. ,
, 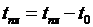 , где F есть оптимальная траектория движения (возможно пересчитанная на предыдущем шаге), t0 – текущий момент времени. Переход к шагу 2.
, где F есть оптимальная траектория движения (возможно пересчитанная на предыдущем шаге), t0 – текущий момент времени. Переход к шагу 2. ,
, 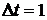 – задают целевой прямоугольник. Ниже приведено графическое представление задачи:
– задают целевой прямоугольник. Ниже приведено графическое представление задачи: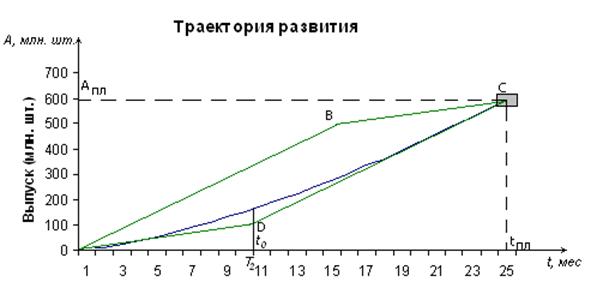
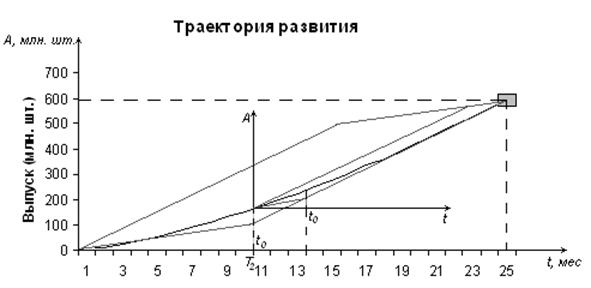
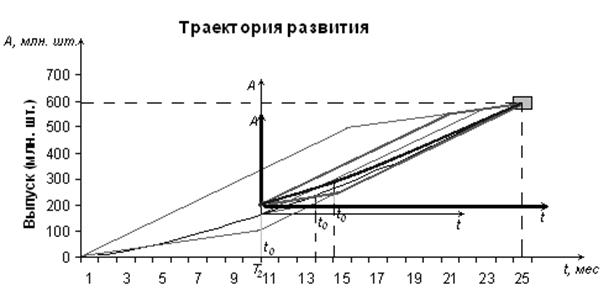
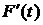 , а затем решая задачу (1)-(6) с новыми параметрами Aпл, tпл определяем очередной момент контроля t0=14.
, а затем решая задачу (1)-(6) с новыми параметрами Aпл, tпл определяем очередной момент контроля t0=14.