
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие сложности. Сложные системыОбъект или систему будем называть сложной, если выполнено одно из свойств: 1. элементы системы, которые можно назвать подсистемами или рядовыми элементами, сами являются системами. 2. система является крупномасштабной, состоит из большого числа элементов и разнообразной системы связей между элементами. Система считается крупномасштабной, если объем информации для описания элементов и связей между ними равен числу Баавермана 3. реакция системы на однотипный вход неоднозначна и часто определяется как нечеткая. При анализе систем используется 3 типа сложности: 1. организованная простота; 2. неорганизованная сложность; 3. организованная сложность. К первому типу задач относятся задачи моделирования сложных процессов на основе выделения основных закономерностей, характеристик и параметров, обеспечивающих достижение цели с минимальными информационными, техническими и материальными средствами. Примерами таких задач являются модель межотраслевого баланса, модель Новожилова, Канторовича, модели смешивания, развития и размещения отраслей. К задачам неорганизованной сложности относятся задачи, которые могут быть решены на основе исследования статистических закономерностей, причем каждый исследуемый элемент рассматривается как статистическая единица, а не как индивидуальный элемент. Самые сложные задачи – задачи организованной сложности, когда в качестве объекта исследования выступают отдельные единицы и взаимосвязи между ними, причем, чем больше единиц и глубже взаимосвязь, тем система сложнее. В качестве одной из основных характеристик сложности выступает мера сложности. Пусть задана некоторая система  1. 2. Если 3. Если Меры сложности изоморфных систем равны: Построение меры сложности любой системы включает в себя следующие этапы: 1. расчет числа элементов системы; 2. определение набора характеристик каждого элемента, необходимых для описания системы; 3. определение возможного числа состояний каждой характеристики; 4. расчет общее число единиц необходимое для описания системы; 5. выбор функции, удовлетворяющей требованиям меры, с помощью которой можно рассчитать сложность системы. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 308. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.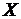 . Функция
. Функция  является мерой сложности системы
является мерой сложности системы  .
.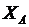 подсистема
подсистема  (
( 
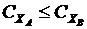 .
.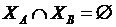 , то
, то  .
.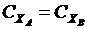 , если
, если  ), то
), то