
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функционирование целевых систем: понятие, описатели, примеры.Стр 1 из 11Следующая ⇒ ОСНОВЫ ТЕОРИИ СИСТЕМ И ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ СИСТЕМНОГО АНАЛИЗА
Методическое пособие для вузов
(издание переработанное и дополненное)
Составители: Н.Б. Баева, Д.В. Ворогушина, Е.В. Куркин
Издательско-полиграфический центр Воронежского государственного университета 2011
Утверждено научно-методическим советом факультета ПММ ВГУ от 25.05.11, протокол № 9
Рецензент профессор кафедры вычислительной математики и прикладных информационных технологий факультета прикладной математики, информатики и механики Т.М.Леденева
Рекомендуется для студентов 2 курса специальности бизнес-информатика и 4 курса специальности прикладная математика и информатика дневного отделения факультета прикладной математики, информатики и механики
Для специальностей: 010501 – Прикладная математика и информатика, 080700 – Бизнес-информатика
Содержание
§1. Основы проектирования систем…………………………………………....4 1.1. Основные понятия и факты. Простейший описатель системы…...4 1.2. Функционирование целевых систем: понятие, описатели, примеры……………………………………………………………….....13 1.3. Динамические системы: сущность, структура, классификация, способы описания. Система как черный ящик…………………………….…20
§2. Основы квалиметрии…………………………………………………….…31 2.1. Понятие качества. Качество ресурсов и качество результата……31 2.2. Методы оценки качества на основе измерения свойств объекта……………………………………………………………….. 31 2.3. Оценка качества объекта на основе коэффициентов  «трудности»…………………………………………………………………….33 2.4. Операционные основы построения производственно-квалитативных функций……………………………………………………….37 2.5. Управление качеством функционирования системы………….....42
§3. Основы теории управления………………………………………………..49 3.1. Понятие сложности. Сложные системы………………………......49 3.2. Управление сложными системами. Типы управления…………...51 3.3. Основная формула теории управления с обратной связью и ее приложения. Мультипликатор Кейнса…………………………………53 3.4. Модели контроля в системах управления…………………………59 3.4.1. Метод выбора точек неравномерного контроля………………...59 3.4.2. Модель равномерного контроля на основе трудности достижения цели ……………………………………………………………….61 3.4.3. Модели выбора оптимального набора контрольных мероприятий………………………………………………………………….....66
Литература………………………………………………………………………73
Основы проектирования систем. Основные понятия и факты. Простейший описатель системы В настоящее время нет единого определения понятия «система». Основоположник теории систем Людвиг фон Берталанфи определял систему как комплекс взаимодействующих элементов или как совокупность элементов, находящихся в определенных отношениях друг с другом и со средой. А. Холл понимал под системой множество предметов вместе со связями между предметами и между их признаками. Начиная с основоположника кибернетики У.Р.Эшби в определение понятия «система» наряду с элементами, связями и их свойствами и целями начинают включать наблюдателя. Под системой ( Элемент ( Подсистема – совокупность элементов, находящихся между собой в более тесных связях, принадлежащих системе в целом и способных выполнять относительно независимые функции, подцели. Система может быть разделена на элементы не сразу, а последовательным расчленением на подсистемы, которые представляют собой компоненты более крупные чем элементы, и в то же время более детальные, чем система в целом. Каждый элемент системы характеризуется некоторым набором свойств. Под свойством элемента ( При выделении элементов необходимо придерживаться следующих принципов: 1. Принцип целесообразности. Необходимо оценивать влияние элемента на конечную цель исследования системы. 2. Принцип минимальной достаточности. Для описания оригинала любой природы в виде системы используется минимально необходимое число элементов, обеспечивающее достижение цели исследования. 3. Принцип «часть-целое». Элемент системы и система в целом должны быть совместимы. Множество свойств системы Следует отметить, что характеристики системы не являются простой суммой характеристик свойств элементов, составляющих эту систему. Система может обладать характеристиками, которыми не обладает ни один из элементов, составляющих ее. Пусть Состояние – определенное значение, набора наиболее существенных показателей или свойств, которые приняты для оценки элемента ( Взаимодействие элементов в системе осуществляется по средствам связей. Связь Когда один элемент вступает в отношения с другим элементом, он теряет часть своих свойств и одновременно приобретает новые. Различают нейтральные и направленные связи, усиливающие и замедляющие, сильные и слабые. По характеру связи бывают равноправные, генетические, связи подчинения, управления; по месту приложения – внутренние и внешние, по направленности в системе – прямые и обратные. Особое место занимает обратная связь, как правило, замыкающая цепь. Ее наличию предшествует контроль состояния элементов. Внутренняя структура системы определяется перемещениями потоков от одних элементов к другим (отношениями между элементами). Структура объекта (процесса, явления) отражает наиболее существенные взаимоотношения между элементами и их группами (подсистемами), которые мало меняются при изменениях в системе и обеспечивают существование системы и ее свойств. Структура - это совокупность элементов и соединяющие их связи. Структура является основой целостности системы и представляет собой мало изменяющуюся категорию. Структуру системы обозначают следующим образом Для задания системы используются описатели. Простейший описатель системы имеет вид В зависимости от количества учитываемых факторов и степени абстрактности понятия «система» меняются ее описатели. Пример 1. Составим простейший описатель системы воспитания/образования в России. В качестве элементов выберем основные воспитательные и образовательные институты, а связи определим как возможность перехода из одного в другой. Элементы системы
Структура системы имеет вид
где Т.о. система воспитания и образования в России описана. Очевидно, что элементы сами являются крупными системами. Так дошкольное воспитание состоит из яслей, детского сада; школа включает в себя начальную школу, среднюю (до 9 класса), высшую (10-11 класс) и т.д. Т.е. выделенные элементы можно рассматривать как подсистемы. Более детальное описание системы имеет вид.
Связи представлены на рисунке.
Матрица, описывающая структуру системы, выписывается по графу, аналогично рассмотренному выше случаю. Пример 2. Опишем с помощью простейшего описателя систему, соответствующую модели Леонтьева. Пусть
В матричном виде:
здесь Элементами в данной задаче будут отрасли Пример 3. Составим простейший описатель системы, заданной оптимизационной задачей. Рассмотрим для простоты задачу линейного программирования,
Построим допустимое множество задачи
Точка (0,0) удовлетворяет неравенству (1) (0
Аналогично строим области заданные неравенствами (2)-(4). Т.о. построено множество
Из рисунка видно, что при увеличении константы С, прямая В данной задаче элементами являются вершины допустимого множества
А структура системы – граница допустимого множества, т.е. неравенства, участвующие в образовании граничных точек ((2)-(4)), записываемые как равенства. Т.о. построен простейший описатель системы (1)-(4). Пример 4. Рассмотрим случай, когда описывается как система многомерная задача линейной оптимизации. Аналогично с предыдущем примером элементами будут вершины допустимого множества, связями – все равенства и неравенства, которыми они связаны, а структурой – неравенства (записываемые как равенства), участвующие в образовании вершин допустимого множества. Если переменных больше двух( 1. Выписать все комбинации из 2. Каждую систему неравенств записать как систему равенств. Если система разрешима, найти решение. 3. Проверить удовлетворяют ли найденные в п.2 точки неравенствам, не входящим в систему, из которых точки были найдены. 4. Если точка удовлетворяет всем неравенствам, записать ее рядом с уравнениями, из которых она была найдена. 5. Найденные таким образом точки – вершины многогранника, а значит - элементы системы. 6. Структура состоит из уравнений, около которых записано не менее Рассмотрим построение простейшего описателя системы для следующей задачи
Здесь
Т.о. элементы системы Задачи 1.Постройте простейший описатель системы управления университетом: выделите элементы (ректор, проректоры…), связи, задайте структуру, подсистемы. 2.Опишите как систему карту дорог Воронежской области: опишите элементы, связи, структуру. Выберите не менее 7 населенных пунктов, а также учтите разные виды дорог (асфальтированная, грунтовая, железная дорога). 3.Представьте устройство компьютера в виде простейшей системы. Выделите не менее 9 элементов, определите различные типы связей (прямые, обратные, нейтральные, связи управления), подсистемы и связи между ними, опишите структуру системы. 4.Три отрасли выпускают продукцию, известна матрица коэффициентов прямых затрат и вектор конечного продукта
Составьте модель Леонтьева, опишите систему. 5.Четыре отрасли выпускают продукцию, известна матрица коэффициентов прямых затрат и вектор конечного продукта
Составьте модель Леонтьева, опишите систему. 6.Составьте простейшие системные описатели следующих оптимизационных задач
А.
В. 7. Предприятие выпускает 2 вида продукции 8. Решите задачу аналогичную задачи 7, если 9. Предприятие выпускает два вида продукции, используя три ресурса. Матрица производственных затрат 10. Кондитерская фабрика выпускает шоколадные конфеты двух видов. Для выпуска используются два основных продукта: какао-порошок и какао-масло, имеющиеся на предприятии в объеме 14 и 10 ц. Затраты продуктов на производство конфет 11. Потребность в азотных удобрениях составляет 10 т. Производится два вида удобрений: аммиачная селитра и аммиачная вода. Для их производства используется аммиак, расход которого не должен превышать 8 т. Суммарные капиталовложения в производство не должны превышать 42 тыс.руб. Технологические нормы материальных затрат, удельные капиталовложения, себестоимость даны в таблице
Определить план производства селитры и аммиачной воды с наименьшими суммарными затратами. Выписать простейший описатель системы. 12. На звероферме могут выращиваться черно-бурые лисы, нутрии и норки. Для их питания используются два вида кормов. В таблице приведены нормы расхода кормов, их ресурс в расчете на день, а также прибыль от реализации одной шкурки каждого зверя.
Построить математическую модель для определения того, сколько и каких зверьков следует выращивать на ферме, чтобы прибыль от реализации шкурок была максимальной. Выписать простейший описатель системы. 13. Для производства 3-х видов продукции используется 3 вида сырья и трудовые ресурсы. Запасы сырья: 100, 200, 150. Матрица затрат сырья на единицу производимой продукции имеет вид Функционирование целевых систем: понятие, описатели, примеры. Система называется функционирующей, если на нее оказывает влияние внешняя среда и если система, в свою очередь, передает во внешнюю среду поток, который соответствует сущности (миссии) системы. Для описания функционирующей системы необходимо ввести характеристики, связывающие систему с внешней средой. К ним относятся – входы и выходы системы, а также передаточная функция.
Обозначим через Описатель функционирующей системы имеет вид
Если сформулирована цель работы системы, то говорят о целевой функционирующей системе. Вводится функция цели
здесь Каждой функционирующей системе можно поставить в соответствие модель, которая состоит в отыскании такого входного потока
Модель считается разработанной, если определены множества Компоненты входного потока системы могут быть разнородными, измеряться в различных шкалах или единицах измерения. Чтобы учесть возможность разнородности компонент, необходимо произвести их фильтрацию с помощью фильтрующего устройства (
Схема 1. Элементарный преобразователь Если система способна переходить из одного состояния в другое, то говорят, что она обладает поведением. Поведение системы во многом зависит от состояния внешней среды – множества элементов, не входящих в систему, изменение состояния которых меняет поведение системы. Рассмотрим переход системы из одного состояния в другое. Пусть известен вектор начальных состояний
Т.о. состояние системы зависит от предыдущего состояния, от влияния окружающей среды, внутренних характеристик системы и входного потока. Важным свойством систем является способность находиться в состояние равновесия, т.е. при отсутствии внешних возмущающих воздействий сохранять свое состояние сколь угодно долго. Пусть на вход системы подается поток
Когда переход к новому состоянию не меняет выходной поток, говорят об устойчивости системы. Целевые системы называются устойчивыми, если из принадлежности входа определенному множеству Пример 1. Модель Леонтьева, с известной матрицей затрат Модель Леонтьева в матричном виде Пример 2. Найти максимум функции
Опишем данную оптимизационную задачу как функционирующую систему. Выпишем для данной задачи следующий описатель
Решение
Определим теперь входы и выходы системы. В общем виде данную задачу можно записать следующим образом
где
Приведем схему функционирования описанной системы
Следует заметить, что если решается задача, сводящаяся к оптимизационной, например, поиск оптимального ассортимента выпуска продукции с использованием ресурсов (задача 7 п. 1.1), часть параметров описанных выше как входные, могут считаться состояниями (внутренними характеристиками) системы, например, матрица Пример 3. Проверить, в какое состояние необходимо перейти системе, описание, которой приведено в предыдущем примере. Если считать, что ее начальное состояние характеризовалось параметрами ( 1. 2. 3. Опишите функционирование системы с помощью схемы. Логично предположить, что переход в новое состояние для системы, описываемой оптимизационной задачей, возможен, если значение функции цели улучшается на оптимальном плане при решении задачи с учетом нового состояния системы.
В какое состояние возможен переход для рассматриваемой системы определите самостоятельно (см. задачу 5), воспользовавшись схемой. Задачи 1.Две отрасли, конечный продукт которых составляет 120 и 70 единиц производят продукцию. Затраты на производство заданы матрицей 2.Три отрасли, конечный продукт которых 100, 200 и 150 единиц производят продукцию. Затраты на производство заданы матрицей 3.Составьте систему формирования валовых выпусков территориального экономического объекта, если рассматриваются 3 отрасли, конечный продукт которых
Выписать модель Леонтьева, составить простейший описатель системы, описать функционирование данного объекта с помощью схемы. 4.Составьте описатели функционирующих систем a)-г) в задаче 6 §1.1. 5.Выберите, в какое состояние необходимо перейти системе, описание которой приведено в примере 3. 6.Проверьте, в каком из приведенных состояний входных параметров (
где Опишите функционирование системы с помощью схемы, при условии, что необходимо запоминать все состояния, в которые возможен переход, а не только лучшее, как в разобранном примере 3. 7.Опишите как функционирующую систему процесс решения следующей оптимизационной задачи
Определить, возможен ли переход в новое состояние 8.Задана матрица коэффициентов прямых затрат Замечание. В данной задаче состояния характеризуются векторами конечного продукта, при этом переход в новое состояние возможен, если трудовые затраты ( |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 488. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ) будем понимать совокупность элементов, вступающих в отношения друг с другом и обладающих целостностью и единством.
) будем понимать совокупность элементов, вступающих в отношения друг с другом и обладающих целостностью и единством.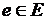 ) – неделимая часть системы, определяемая на основе заранее введенных общих принципов, для которых известны основные характеристики.
) – неделимая часть системы, определяемая на основе заранее введенных общих принципов, для которых известны основные характеристики.  - множество элементов системы. Элемент является пределом разбиения системы с точки зрения решения конкретной задачи и поставленной цели. Элементы системы могут задаваться, например, простым перечислением, множеством.
- множество элементов системы. Элемент является пределом разбиения системы с точки зрения решения конкретной задачи и поставленной цели. Элементы системы могут задаваться, например, простым перечислением, множеством. ) понимают характеристику, которая может быть определена с помощью набора операций или измерена с помощью какого-то инструмента.
) понимают характеристику, которая может быть определена с помощью набора операций или измерена с помощью какого-то инструмента.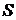 будем обозначать
будем обозначать  . Тогда справедливо следующее включение
. Тогда справедливо следующее включение  .
. - множество элементов, составляющих систему
- множество элементов, составляющих систему  .
. ), системы (С(S)) или подсистемы.
), системы (С(S)) или подсистемы. 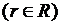 – некоторое отношение, возникающее между элементами. Связи задаются, как правило, отношениями (матрицами, графами, сечениями).
– некоторое отношение, возникающее между элементами. Связи задаются, как правило, отношениями (матрицами, графами, сечениями). .
. .
. , где - дошкольное воспитание;
, где - дошкольное воспитание;  -школа;
-школа;  -среднее образование;
-среднее образование; 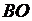 - высшее образование. Связи опишем графом.
- высшее образование. Связи опишем графом.



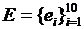 , где
, где  - ясли,
- ясли,  - детский сад,
- детский сад,  - начальная школа,
- начальная школа, 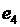 - средняя,
- средняя,  -высшая школа,
-высшая школа,  -колледж,
-колледж,  - бакалавриат,
- бакалавриат,  - магистратура,
- магистратура,  - специалисты.
- специалисты.
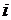 -порядковый номер «чистой» отрасли, производящей продукт,
-порядковый номер «чистой» отрасли, производящей продукт, 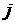 - потребляющий продукт (
- потребляющий продукт (  ). Под «чистой» понимается отрасль, выпускающая(потребляющая) один единственный продукт. Обозначим через
). Под «чистой» понимается отрасль, выпускающая(потребляющая) один единственный продукт. Обозначим через - валовой выпуск
- валовой выпуск  -конечный продукт
-конечный продукт  -ой отрасли;
-ой отрасли;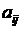 -количество (в стоимостном выражении) продукции
-количество (в стоимостном выражении) продукции 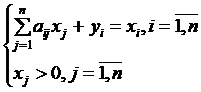 .
. ,
, - матрица коэффициентов прямых затрат,
- матрица коэффициентов прямых затрат, 
 - вектор валовых выпусков,
- вектор валовых выпусков,  - вектор конечного продукта,
- вектор конечного продукта, 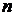 .
. . Связи определяются коэффициентами прямых затрат
. Связи определяются коэффициентами прямых затрат  - элемент
- элемент  - связи между элементами нет. Структура задается матрицей
- связи между элементами нет. Структура задается матрицей 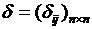 ,
,  .
.

 (1)
(1)
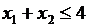 (2)
(2) (3)
(3) (4)
(4) . Данная прямая проходит через точки
. Данная прямая проходит через точки 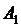 ,
, 

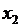
 4
4 13), принадлежит искомой плоскости, значит, полуплоскость под прямой задается неравенством (1)
13), принадлежит искомой плоскости, значит, полуплоскость под прямой задается неравенством (1)
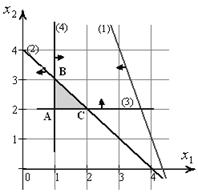

 , с вершинами
, с вершинами  ,
,  ,
,  .Найдем максимальное значение функции цели
.Найдем максимальное значение функции цели  на данном множестве. Для этого построим любые две линии уровня функции
на данном множестве. Для этого построим любые две линии уровня функции  ), например,
), например, 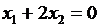 и
и  (т.е.
(т.е. 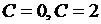 ). Таблицы точек для построения прямых
). Таблицы точек для построения прямых двигается вверх. Параллельным переносом будем сдвигать прямую
двигается вверх. Параллельным переносом будем сдвигать прямую  , максимальное значение функции цели на допустимом множестве
, максимальное значение функции цели на допустимом множестве  .
. , связи задаются всеми неравенствами
, связи задаются всеми неравенствами
 .
. ) и решать графически нельзя, предлагается следующий алгоритм нахождения вершин многогранника, заданного системой из
) и решать графически нельзя, предлагается следующий алгоритм нахождения вершин многогранника, заданного системой из  неравенств:
неравенств: систем неравенств.
систем неравенств.
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) . Т.о. необходимо решить 4 системы уравнений. Решение системы (1)-(3) (с заменой знаков неравенств на равенства) - точка
. Т.о. необходимо решить 4 системы уравнений. Решение системы (1)-(3) (с заменой знаков неравенств на равенства) - точка  . Проверим выполнение ограничения (4):
. Проверим выполнение ограничения (4):  .Запишем
.Запишем  , удовлетворяющая неравенству (3):
, удовлетворяющая неравенству (3):  . Из двух других систем уравнений, находим точки
. Из двух других систем уравнений, находим точки  , удовлетворяющие неравенствам, не входящим в системы из которых они найдены.
, удовлетворяющие неравенствам, не входящим в системы из которых они найдены.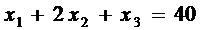
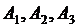

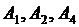
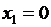



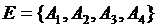 , связи
, связи 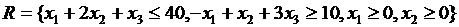 , структура
, структура  .
. ,
, 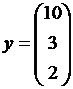 .
. ,
,  .
. Б.
Б. 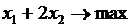



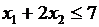
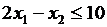
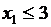
 Г.
Г. 

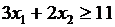



 , используя 2 ресурса
, используя 2 ресурса  . Известны затраты каждого ресурса на выпуск единицы продукции
. Известны затраты каждого ресурса на выпуск единицы продукции  :
:  . Общий объем ресурсов на предприятии
. Общий объем ресурсов на предприятии  . Выпуск каждого вида продукции должен составлять не менее двух единиц, т.е.
. Выпуск каждого вида продукции должен составлять не менее двух единиц, т.е.  ,
, 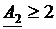 . Затраты времени на производство единицы продукции
. Затраты времени на производство единицы продукции  . Необходимо выпустить продукцию, минимизировав трудовые затраты. Составьте модель решения задачи и выпишите простейший описатель системы для полученной оптимизационной задачи.
. Необходимо выпустить продукцию, минимизировав трудовые затраты. Составьте модель решения задачи и выпишите простейший описатель системы для полученной оптимизационной задачи. ,
,  ,
,  ,
,  ,
, 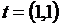 .
.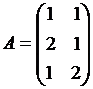 , общий объем ресурсов
, общий объем ресурсов  .Требуется найти максимальный выпуск продукции при использовании данных ресурсов. Составьте модель решения задачи и выпишите простейший описатель системы для полученной оптимизационной задачи.
.Требуется найти максимальный выпуск продукции при использовании данных ресурсов. Составьте модель решения задачи и выпишите простейший описатель системы для полученной оптимизационной задачи. , трудовые затраты
, трудовые затраты  . Вектор затрат трудовых ресурсов
. Вектор затрат трудовых ресурсов  . Минимальная потребность в каждом виде продукции задана вектором
. Минимальная потребность в каждом виде продукции задана вектором  . Выписать простейший описатель системы.
. Выписать простейший описатель системы.
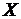 - набор входных переменных,
- набор входных переменных, 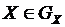 ,
, 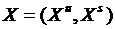 ,
,  -управляемые переменные;
-управляемые переменные; 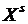 - случайные переменные. Система характеризуется состояниями, внутренними характеристиками
- случайные переменные. Система характеризуется состояниями, внутренними характеристиками 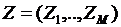 , которые могут быть измерены в любой момент времени.
, которые могут быть измерены в любой момент времени.  ,
,  - множество возможных состояний системы.
- множество возможных состояний системы.  - передаточная функция системы – оператор, позволяющий рассчитывать выходную переменную
- передаточная функция системы – оператор, позволяющий рассчитывать выходную переменную 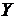 ,
,  ,
,  . Система функционирует, если она переходит из одного состояния в другое.
. Система функционирует, если она переходит из одного состояния в другое.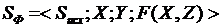 .
. , и описатель системы принимает вид
, и описатель системы принимает вид ,
, - параметры внутренних характеристик системы,
- параметры внутренних характеристик системы,  . Причем, передаточная функция обобщается и зависит не от состояний системы, а от внутренних параметров
. Причем, передаточная функция обобщается и зависит не от состояний системы, а от внутренних параметров 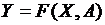 .
. . Модель целевой функционирующей системы имеет вид
. Модель целевой функционирующей системы имеет вид ,
, 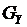 ,
,  , а также
, а также  ), с последующим интегрированием чистых потоков. Объединение (суммирование) потоков происходит в сумматоре (
), с последующим интегрированием чистых потоков. Объединение (суммирование) потоков происходит в сумматоре (  ), затем выходной поток направляется во внешнюю среду распределителем
), затем выходной поток направляется во внешнюю среду распределителем  . Такая система называется элементарным преобразователем.
. Такая система называется элементарным преобразователем.
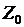 . Обозначим
. Обозначим  - порядковый номер состояния,
- порядковый номер состояния,  ;
;  - вектор влияния внешней среды на систему, тогда поведение системы определяется следующим образом
- вектор влияния внешней среды на систему, тогда поведение системы определяется следующим образом .
. и
и 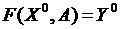 . Точка
. Точка  , точка выхода
, точка выхода  :
: .
. , следует, что изменение выходного потока будет лежать в пределах заданного множества выходных потоков
, следует, что изменение выходного потока будет лежать в пределах заданного множества выходных потоков  . Под устойчивостью понимается способность системы возвращаться в состояние равновесия после того, как она была выведена из него под влиянием внешних возмущающих воздействий.
. Под устойчивостью понимается способность системы возвращаться в состояние равновесия после того, как она была выведена из него под влиянием внешних возмущающих воздействий. , перепишем в виде
, перепишем в виде  . Т.о. входной поток – вектор конечного потребления (
. Т.о. входной поток – вектор конечного потребления (  , а передаточная функция
, а передаточная функция  . Т.о.
. Т.о.  .
. при условии
при условии
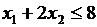 (1)
(1) (2)
(2) (3)
(3) . Простейший описатель
. Простейший описатель  определяется аналогично примеру 3 из 1.1. Допустимое множество данной задачи и линии уровня функции цели представлены на рисунке.
определяется аналогично примеру 3 из 1.1. Допустимое множество данной задачи и линии уровня функции цели представлены на рисунке.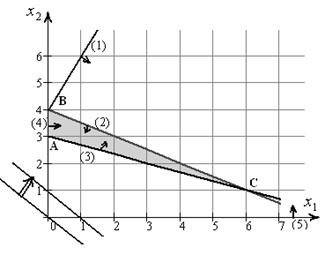
 ,
,  .
. ,
, 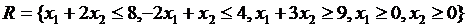 ,
,  .
.
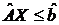
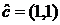 ,
,  ,
,  . Тогда входами системы являются
. Тогда входами системы являются 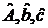 , выходы – решение задачи
, выходы – решение задачи  , передаточная функция – процесс решения задачи, например, в линейном случае, это может быть симплекс-метод (с-м). Получаем следующий описатель системы
, передаточная функция – процесс решения задачи, например, в линейном случае, это может быть симплекс-метод (с-м). Получаем следующий описатель системы

 характеризует технологический процесс и является внутренней характеристикой системы. В случае изменения состояний системы на схеме появляются обратные связи.
характеризует технологический процесс и является внутренней характеристикой системы. В случае изменения состояний системы на схеме появляются обратные связи. ), а три новых состояния (
), а три новых состояния (  ) определяются параметрами (
) определяются параметрами (  ):
): ;
;  :
:  ,
,  ,
, 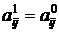 ,
,  ,
,  =
=  ;
;  =
=  .
. ;
; 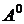 ;
;  ,
,  ;
;  ;
;  ,
,  .
. Опишем процесс решения задачи как функционирование системы с помощью схемы для случая, когда задача линейного программирования записана в произвольном виде и рассматривается возможность перехода в
Опишем процесс решения задачи как функционирование системы с помощью схемы для случая, когда задача линейного программирования записана в произвольном виде и рассматривается возможность перехода в  новых состояний.
новых состояний. . Составьте модель Леонтьева, найдите валовой выпуск отраслей, выпишите описатель функционирующей системы.
. Составьте модель Леонтьева, найдите валовой выпуск отраслей, выпишите описатель функционирующей системы. . Составьте модель Леонтьева, найдите валовой выпуск отраслей, выпишите описатель функционирующей системы.
. Составьте модель Леонтьева, найдите валовой выпуск отраслей, выпишите описатель функционирующей системы. , а матрица производственных затрат
, а матрица производственных затрат  . Матрица, характеризующая в данной задаче состояния системы, меняется следующим образом
. Матрица, характеризующая в данной задаче состояния системы, меняется следующим образом ,
, 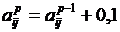 ,
,  ,
,  .
. ), значения выходных параметров (
), значения выходных параметров ( 




 ,
,  ,
,  ,
,  .
. 



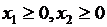
 ,
, 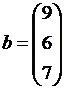 .
. , трудовые затраты
, трудовые затраты 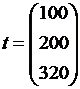 , вектор конечного продукта
, вектор конечного продукта  . Известны допустимые вектора конечного продукта
. Известны допустимые вектора конечного продукта  ,
,  ,
, 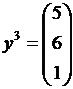 . Определить, в какое из 3 состояний системы возможен переход. Описать функционирование системы с помощью схемы и описателя.
. Определить, в какое из 3 состояний системы возможен переход. Описать функционирование системы с помощью схемы и описателя. ) не увеличатся.
) не увеличатся.