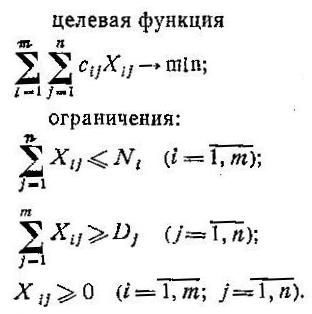Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моделирование задач управления производствомСущность моделирования заключается в создании такого аналога Изучаемого объекта или процесса, в котором отражены важнейшие точки зрения исследования свойства и не учитываются второстепенные. В практике управления при решении различных задач можно встретить все методы моделирования и все типы моделей. Модель представляет собой отображение определенного объекта, с помощью которого воспроизводятся его существенные признаки. Особое место в построении экономико-математической модели принадлежит выбору критерия оптимальности (экономического показателя эффективности, экстремального или другого определенного значения, которого необходимо достичь). Показатель эффективности выбирается исходя из сущности поставленной задачи. Прежде всего, необходимо ориентироваться на показатели, характеризующие народнохозяйственную эффективность моделируемого объекта. Для задач, решаемых методами математического программирования, уравнение критерия оптимальности называется уравнением цели, или целевой функцией. Каждой решаемой задаче соответствует одна целевая функция. Кроме целевой функции в модель входит ряд уравнений и неравенств, определяющих систему ограничений, накладываемых внешней по отношению к моделируемому объекту средой. Построению математической модели должен предшествовать всесторонний количественный и качественный анализ поставленной задачи управления. Этот анализ должен осуществляться в соответствии с принципами системного подхода. В результате анализа должны быть выявлены все существенные элементы задачи и их взаимосвязи. После этого переходят к построению экономико-математической модели: определяются необходимые входные данные, состав выходной информации, устанавливается математическая связь между отдельными элементами задачи. Чрезмерное усложнение и излишняя степень детализации модели могут привести к тому, что возможности ЭВМ окажутся недостаточными для решения поставленной задачи.  Основное внимание при количественном анализе уделяется определению чувствительности решения к вариациям различных характеристик модели, в том числе к вариациям входных данных и структурных компонентов. Применение экономико-математических методов и электронно-вычислительной техники в управлении производством существенно повышает обоснованность управленческих решений. К экономико-математическим методам относят методы математического программирования (линейного, нелинейного, целочисленного, динамического), а также сетевые методы планирования и управления, методы теории массового обслуживания, экстраполяции, системного анализа, статистического контроля, управления в динамических системах, игровые методы, методы имитационного моделирования, статистического моделирования и др. Сущность экономико-математических моделей можно рассмотреть на следующих примерах. Пример 1. Предприятие выпускает три различных вида продукции (I, II и III), каждый из которых получается путем определенной переработки одного и того же сырья. Сырье может поставляться двумя различными поставщиками. При этом объемы продукции I, II и III, которые можно получить из единицы сырья, различны в зависимости от поставщика сырья (значения характеристик сырья различны). Различна относительная прибыль предприятия в зависимости от поставщика. При принятии решения о количестве сырья, закупаемого у каждого из поставщиков (1 в 2), должны также учитываться еще два фактора: план выпуска каждого продукта н максимальное количество продукции каждого вида, которое предприятие может изготовить при заданных условиях производства. Оба эти фактора должны быть учтены соответствующими ограничениями. Оптимальным следует считать управленческое решение о количествах сырья (N1 и N2), закупаемого у каждого поставщика, при которых относительная прибыль предприятия максимальна. Исходные условия задачи представлены в табл. 16.1.
Таблица 16.1. Выход продукции на единицу объема перерабатываемого сырья
В таблице приняты следующие обозначения: а, b, c – относительные количества (доли) соответствующего вида продукции (I, II, III), которые можно получить из единицы объема сырья поставщика 1; a+b+c+d = 1, где d — доля отходов при изготовлении продукции из сырья поставщика 1; е, f, g — относительные количества соответствующего вида продукции (I , II или III), которые можно получить из единицы объема сырья поставщика 2; e+f+g+h = 1, где h — доля отходов при изготовлении продукции из сырья поставщика 2. Удельная относительная прибыль - это прибыль предприятия от реализации продукции, изготовленной из единицы объема сырья. Математическая модель задачи имеет следующий вид: целевая функция AN1+BN2 ограничения: aN1+eN2 ≤ X; bN1+fN2 ≤ Y; cN1+gN2 ≤ Z; N1 ≥ 0; N2 ≥ 0 Условия неотрицательности количества сырья, поставляемого каждым поставщиком N1 ≥ 0; N2 ≥ 0 приняты потому, что отрицательные значения этих величин не имеют физического смысла. Рассмотренная задача служит иллюстрацией модели линейного программирования и может быть решена симплексным методом. В случаях практического применения линейного программирования количество ограничений обычно достигает нескольких сотен, а количество переменных нескольких тысяч. Поэтому решение практических задач предполагает использование ЭВМ. Пример 2. Необходимо определить оптимальные объемы выпускаемой продукции для каждого промышленного предприятия, входящего в некоторое множество однотипных предприятий, за заданный интервал времени. Пусть отрасль, имеющая N промышленных предприятий, должна выпустить Д единиц однородной продукции в течение заданного интервала времени (например, за пятилетку). Следовательно, если обозначить через Xj объем продукции, выпускаемой на промышленном предприятии j, то Xl+X2+...+XJ+...+XN = D, (6.1) Где Xj≥0 для Если стоимость производства продукции Xj на предприятии выразить как Xj2/Cj (где Cj≥0 — постоянная для данного предприятия величина, характеризующая уровень технологии, организации труда, производства и управления), то оптимальные значения Xj находятся из условия:
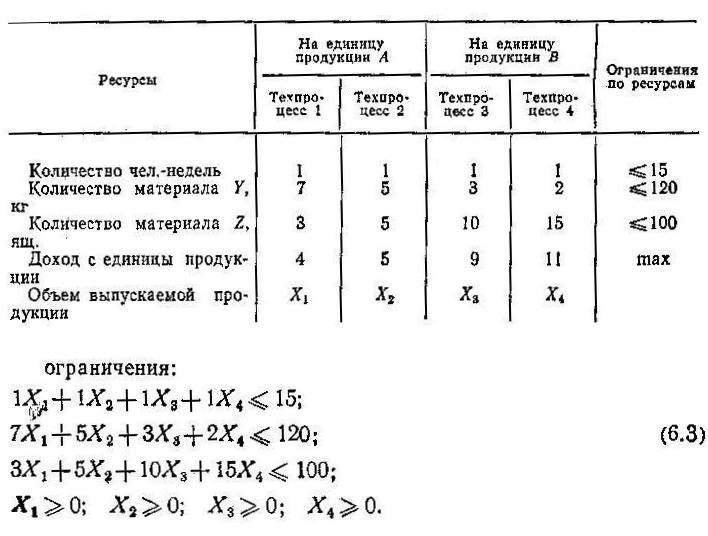
Эта задача оптимизации может быть решена методами динамического программирования, а также с помощью некоторых приемов нелинейного программирования. Пример 3. Необходимо определить оптимальные объемы продукции, выпускаемой одним предприятием в течение нескольких периодов времени. Пусть Xj — объем продукции, выпускаемой предприятием в течение периода времени j; М — количество рассматриваемых периодов времени; Д — количество единиц продукции, которое должно выпустить предприятие за все рассматриваемые периоды времени. Математическая постановка н возможные методы решения те же, что и в предыдущем примере. При этом рассматриваются лишь затраты, связанные с производством, и не учитываются издержки, обусловленные хранением продукции в интервале между началом 1-го и концом j-го периодов (пока весь объем продукции Д не будет полностью реализован). Пример 4. На предприятии, выпускающем неоднородную продукцию, руководитель стремится определить, какими должны быть уровни производства для каждого вида продукции в течение некоторого наперед заданного периода. Эти уровни ограничены технико-технологическими, организационно-экономическими и другими внутренними для данного предприятия условиями. В рамках этих ограничений руководство данного предприятия пытается оптимизировать некоторую конкретную целевую функцию, например, целью является получение максимальной прибыли. Пусть предприятие имеет возможность реализовать от одного до четырех различных типов технологических процессов. Технологические процессы 1 и 2 ориентированы на получение продукции А, а технологические процессы 3 и 4 — на получение продукции В. Поскольку затраты, связанные с различными технологическими процессами, неодинаковы, прибыльность процессов оказывается разной даже в том случае, когда они используются для получения продукции одного и того же вида. Производственно-экономические показатели и ограничения приведены в табл. 16.2. Математическая модель задачи имеет следующий вид: целевая функция
T а блиц а 21.2. Исходные данные для составления оптимального плана предприятия
Задача организованного управления заключается в том, чтобы найти значения всех неизвестных (X1, X2, X3, X4), удовлетворяющие соотношениям ф.6.3. и максимизирующие прибыль (ф.6.2). Данная задача как в примере 1 может быть решена симплексным методом. Пример 5. Отрасль имеет m промышленных предприятий, которые находятся в различных географических районах страны и выпускают одинаковую продукцию, являющуюся сырьем для n других промышленных предприятий, также расположенных в различных географических районах. Ежедневное производство сырья на заводе i (i=1,m) не превышает Ni единиц (например, т.) Чтобы удовлетворить имеющийся на сырье спрос отрасль должна ежедневно поставлять на каждый из n заводов не менее Дj (j= Пусть Xij – количество сырья, поставляемого потребителю j заводом i, а cij – соответствующие транспортные расходы в расчете на единицу сырья. Математическая задача формируется следующим образом:
Такая задача называется транспортной. Она является частным случаем общей задачи линейного программирования и имеет собственный алгоритм решения, хотя может быть решена и симплексным методом. Пример 6. Предприятие должно разработать календарный план выпуска некоторого вида изделий на плановый период, состоящий из N отрезков. Предполагается, что для каждого из этих отрезков известен точный объем реализации этих изделий. Время изготовления партии изделий бесконечно мало по сравнению с каждым из отрезков планового периода, т. е. изделия, изготовленные в течение отрезка t, могут быть использованы для полного или частичного покрытия спроса в течение этого же отрезка. Для разных отрезков спрос неодинаков. На экономические показатели производства влияют размеры изготавливаемых партий. Поэтому нередко бывает выгодно изготовить в течение некоторого месяца изделий больше, чем это необходимо, и хранить готовые изделия, используя их для удовлетворения последующего спроса. Вместе с тем хранение готовых изделий связано с определенными затратами. Эти затраты в общем случае обусловлены такими факторами, как проценты за банковский кредит, взятый для возможности создания запасов, арендная плата за складские помещения, страховые взносы и расходы по содержанию готовых изделий. Перечисленные выше затраты необходимо учитывать при разработке производственной программы. Программа должна быть такой, чтобы общая сумма затрат на производство и на содержание запасов была минимальной при условии полного и своевременного удовлетворения спроса на изделия. Для построения модели необходимо ввести следующие переменные и обозначения: Xt — объем выпуска изделий в течение отрезка периода t; it — уровень запасов на конец отрезка t; Dt — спрос на изделия на отрезке t (предполагается, что к началу планового периода все Dt известны); ct (Xt, it) —затраты на .отрезке t. Предполагается, что для каждого отрезка затраты зависят от выпуска продукции, уровня запасов на конец отрезка и, возможно, от значения t. Математическая модель при принятых обозначениях имеет вид: целевая функция
Если бы все величины затрат ct (Xt, it) линейно зависели от значений переменных, то решение можно было бы найти, используя сетевые методы. Однако в большинстве практических случаев функция затрат нелинейна. Для того чтобы решить задачи при нелинейности каждой ct (Xt, it) необходимо переформулировать ее в терминах динамического программирования (описать рекуррентным соотношением) и воспользоваться рекуррентным алгоритмом. |
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 535. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||
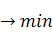 ;
;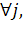 j=
j= 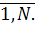
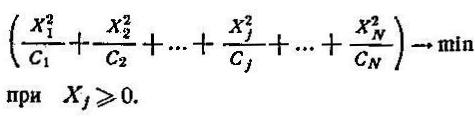
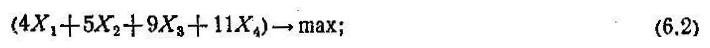
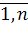 ) единиц сырья. Экономическая задача состоит в том, чтобы рассчитать каких потребителей сырья за какими завозами закрепить, чтобы суммарные транспортные издержки отрасли были минимальными.
) единиц сырья. Экономическая задача состоит в том, чтобы рассчитать каких потребителей сырья за какими завозами закрепить, чтобы суммарные транспортные издержки отрасли были минимальными.