
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы оптимизации в среднемПо меткому замечанию одного из исследователей, методы теории принятия решения дают возможность получать плохие результаты в тех случаях, когда другими способами получить результаты оказывается просто невозможно. Во многом это утверждение можно отнести и к методу сведения задачи к детерминированной. Вполне естественно желание улучшить результаты решения за счет максимально возможного учета характеристик случайного процесса. Считается, что наиболее полная информация о нем содержится в функции распределения. Функция распределения случайной величины
Рис. 19. Пример функции распределения случайной величины В зависимости от вида случайного процесса его функция распределения может описываться самыми разнообразными математическими выражениями. Случайная величина называется дискретной, если она может принимать только конечное или счетное множество значений. Для описания таких функций распределения пользуются, например, биноминальным, гипергеометрическим или пуассоновским распределениями [1]. Непрерывные случайные величины рассматриваются в совокупности с их плотностью распределения
Задание функции распределения случайного параметра предусматривает задание его вида, т.е. собственно математического выражения, и значений параметров, входящих в это математическое выражение. Среди многих известных функций распределения упомянем распределение Гаусса или нормальное распределение, для которого 
Здесь Примечание. Определение вида закона распределения, т.е. математического выражения, описывающего функцию распределения случайной величины, представляет собой самостоятельную задачу исследования, которая выходит за пределы настоящей дисциплины. В то же время если это выражение известно (задано), то параметры закона распределения Методы оптимизации в среднем предусматривают замену ранее выбранного критерия оптимизации. Поскольку параметр принимает случайные значения, рассчитанная на его основе критериальная функция также становится случайной, в связи с чем задача ее максимизации становится бессмысленной. В то же время можно ставить и решать, например, задачу максимизации среднего значения критериальной функции. В литературе [5] этот вариант получил название М‑постановки задачи. Еще одним вариантом постановки задачи можно считать обеспечение некоторого значения целевой функции с заданной вероятностью (Р‑постановка). Для линейной задачи с
где Аналитический метод решения задачи разработки управленческого решения предусматривает непосредственное вычисление выражения (6). На практике, если дополнительно принимать во внимание ограничения, это оказывается весьма затруднительным. Поэтому при изучении настоящей дисциплины аналитический метод использоваться не будет. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 434. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 определяет вероятность того, что значение случайной величины
определяет вероятность того, что значение случайной величины  будет меньше некоторого значения
будет меньше некоторого значения  . На рис. 19 показан пример функции распределения. Отметим, что может быть определена и обратная функция
. На рис. 19 показан пример функции распределения. Отметим, что может быть определена и обратная функция  , которая связывает значения вероятности с аргументом. На рис. 19 стрелками показан процесс вычисления прямой и обратной функции распределения.
, которая связывает значения вероятности с аргументом. На рис. 19 стрелками показан процесс вычисления прямой и обратной функции распределения.
 , где
, где .
. .
. математическое ожидание и
математическое ожидание и  стандартное отклонение ‑ параметры распределения. Особое значение нормального распределения в теории и практике основывается на так называемой центральной предельной теореме. В соответствии с ней, если случайная величина представляется как сумма большого числа не зависящих друг от друга слагаемых, каждое из которых вносит в сумму лишь незначительный вклад, то эта сумма распределена приблизительно нормально [1].
стандартное отклонение ‑ параметры распределения. Особое значение нормального распределения в теории и практике основывается на так называемой центральной предельной теореме. В соответствии с ней, если случайная величина представляется как сумма большого числа не зависящих друг от друга слагаемых, каждое из которых вносит в сумму лишь незначительный вклад, то эта сумма распределена приблизительно нормально [1].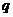 случайными параметрами выражение для функции распределения критериальной функции имеет вид
случайными параметрами выражение для функции распределения критериальной функции имеет вид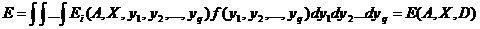 , (6)
, (6) ‑ массив статистических характеристик случайных величин, а
‑ массив статистических характеристик случайных величин, а  ‑ закон распределения вероятностей случайных величин. Как и в случае детерминированной задачи, решение представляет собой некое оптимальное действие
‑ закон распределения вероятностей случайных величин. Как и в случае детерминированной задачи, решение представляет собой некое оптимальное действие  , удовлетворяющее имеющимся ограничениям и обеспечивающее
, удовлетворяющее имеющимся ограничениям и обеспечивающее  . Если функция распределения целевой функции известна, то решение задачи управленческого решения сводится к отысканию значений управляемых параметров
. Если функция распределения целевой функции известна, то решение задачи управленческого решения сводится к отысканию значений управляемых параметров