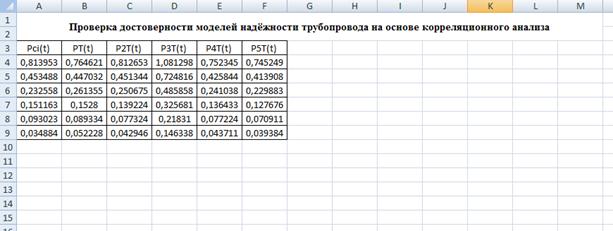
Лабораторная работа №4. Выбор оптимального метода моделирования и модели надежности магистрального трубопровода на базе корреляционного анализа в Microsoft Excel 2007

Цель лабораторной работы

Цель лабораторной работы - приобретение знаний по выбору оптимальной теоретической модели надёжности на базе корреляционного анализа. 

В результате выполнения лабораторной работы обучающийся должен:

- изучить основные теоретические положения, используемые при корреляционном анализе;

- провести ввод данных, расчёт эмпирических показателей надёжности и теоретических моделей надёжности по предыдущим лабораторным работам (№ 1,2,3) в среде Microsoft Excel;

- используя метод «корреляция» в Exсel, оценить модели надежности;

- проанализировать полученные результаты и подготовить отчет о проделанной работе.

Постановка задачи.

Введем следующие обозначения теоретических функций надежности трубопровода, полученных ранее разными методами компьютерного моделирования:

- P_Т (t )— для наименьших квадратов без коэффициента;

- P_2Т (t)— для наименьших квадратов с коэффициентом;

- P_3Т (t)— для линии тренда;

- P_4Т (t)—для экспоненциальной регрессии без коэффициента;

- P_5Т (t)— для экспоненциальной регрессии с коэффициентом.

Для выполнения данной работы следует выбрать новый вариант исходных данных. На рабочих листах Excel просчитать все теоретические модели по лабораторным работам №1,2 и 3.

На последнем рабочем листе Excel подготовим массив исходных данных для проведения корреляционного анализа. Для этого в диапазон ячеек A3-F9 скопируем значения эмпирической и теоретических вероятностей безотказной работы трубопровода: P_сi(t), P_T(t), P_2T(t), P_3T(t), P_4T(t) и P_5T(t). Образ экрана результатов копирования приводится на рис. 4.20.

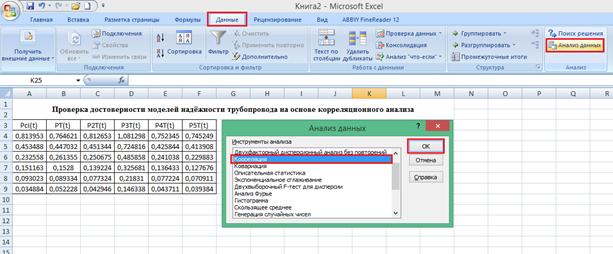
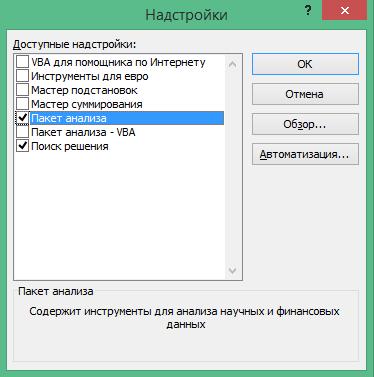
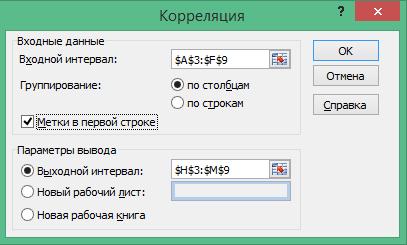
Рис. 4.20 Подготовка массива данных для проведения корреляционного анализа

Доступ к методу «Корреляция» осуществим с помощью выполнения цепочки команд «Данные - Анализ данных — Корреляция» (рис. 4.21). Если во вкладке «Данные» у вас не доступен «Анализ данных», его нужно подключить в надстройках Microsoft Excel 2007 (рис. 4.22).

Заполним поля в открывшемся диалоговом окне метода «Корреляция», образ которого приводится на рис. 4.23.

1. Входной интервал — диапазон ячеек А3 - F9, содержащий массив значений эмпирической и теоретических вероятностей безотказной работы трубопровода.

2. Группирование — это поле указывает на способ записи данных в Excel. Данные могут быть записаны «по столбцам» или «по строкам». Для нашего случая выберем способ записи данных «по столбцам».

Рис. 4.21 Выполнение команд «Данные - Анализ данных — Корреляция»

Рис. 4.22 Подключение надстройки "Пакет анализа"

3. Метки в первой строке —указывает наличие названия (заголовков) столбцов. Отметим это поле «галочкой», чтобы исключить из вычислений первые строки массива данных, содержащие названия столбцов P_сi(t), P_T(t), P_2T(t), P_3T(t), P_4T(t) и P_5T(t).

4. Параметры вывода — указывает место записи результатов анализа: конкретный интервал (диапазон ячеек), новый рабочий лист или книга. Укажем диапазон ячеек H3-N9.

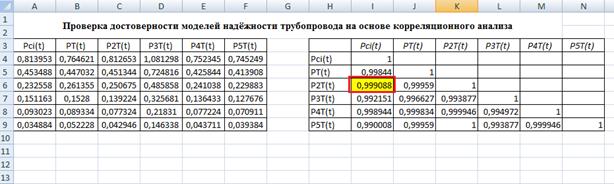
Рис. 4.23 Диалоговое окно метода "Корреляция"

Коэффициенты корреляции R_XY полученные в результате корреляционного анализа моделей надежности трубопровода, отражены в табл. 2, что соответствует образу экрана Excel, приводимого на рис. 4.24.

Таблица 2

Рис. 4.24 Результаты корреляционного анализа надёжности трубопровода

Проанализируем значения первого столбца P_ci(t) табл. 2. Наибольшее значение коэффициента корреляции R_XY = 0.999088 имеет экспоненциальная модель надежности трубопровода «с коэффициентом» P_2T(t), построенная с помощью метода наименьших квадратов.

В итоге проведенных исследований можно сделать следующие выводы:

I. Гипотеза об экспоненциальном законе распределения верна.

II. Все построенные разными методами компьютерного моделирования экспоненциальные модели надежности трубопровода достоверны и имеют весьма высокую тесноту связи с эмпирическими данными (согласно полученным значениям коэффициентов корреляции по шкале Чедокка).

III. Наиболее точной (достоверной) является модель надежности трубопровода «с коэффициентом», построенная методом наименьших квадратов которая имеет следующий вид

P_2T(t)= 1,09 e ^{-0,001960247t}

Оформление отчета

    Отчет должен содержать:

1. Титульный лист с названием работы.

2. Цель и задачи работы.

3. Конспект теоретической части.

4. Расчетные формулы и расчет всех величин.

5. График рассмотренных режимов.

6. Выводы.

Контрольные вопросы

1. Определение надёжности.

2. Какие эмпирические показатели надёжности использовались в работе, объяснить их назначение.

3. Что такое корреляция?

4. Чем проводилась оценка тесноты связи случайных величин?

5. Какие функции среды Microsoft Excel использовались в работе, объяснить их назначение.