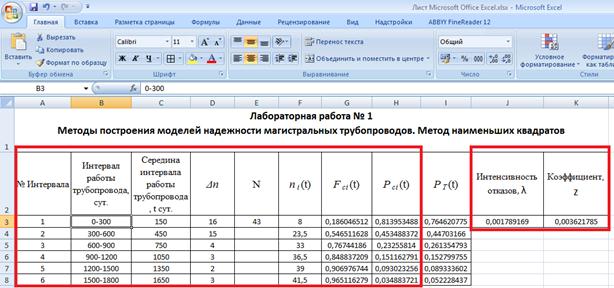
ГЛАВА 4 ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Лабораторная работа №1. Методы построения моделей надежности магистральных трубопроводов. Метод наименьших квадратов

Цель лабораторной работы

Цель лабораторной работы - приобретение знаний по расчёту эмпирических показателей надёжности и теоретической модели надёжности по методу наименьших квадратов. 

В результате выполнения лабораторной работы обучающийся должен:

- изучить основные теоретические положения, используемые при построении моделей надёжности;

- изучить теоретические положения метода наименьших квадратов;

- провести ввод данных, расчёт эмпирических показателей надёжности и теоретической модели надёжности по методу наименьших квадратов в среде Microsoft Excel;

- построить график;

- проанализировать полученные результаты и подготовить отчет о проделанной работе.

Постановка задачи.

Определение теоретической функции надежности (построение модели надежности) в Excel методом наименьших квадратов решается в три этапа.

Этап 1. На рабочем листе Excel подготовим диапазоны для «входной» и «выходной» информации компьютерного моделирования.  Для исходных данных выделим следующие диапазоны ячеек:

- в В3-В8 запишем интервалы работы трубопровода, сут.,

- в С3-С8 запишем значения середины временного интервала, t сут.,

- в D3-D8 запишем  эмпирическую частоту отказов в интервале, Δn,

- в E3 число отказов за весь период наблюдения, N,

- в F3-F8 суммарное число отказов в текущем интервале, вычисленное для середины интервала, n_i(t),

- в G3-G8 эмпирическую вероятность отказов для середины интервала ,

- в С7-С12 запишем значения эмпирических вероятностей безотказной работы трубопровода P_сi(t).

Для заполнения неизвестных исходных данных нужно воспользоваться формулам и для нахождения коэффициентов надёжности представленных в пункте 2.1 (2.1), (2.2), (2.3) и (2.4). Для получения исходных данных по своему варианту см. Приложение 1.

Этап 2. Определяется целевая функция, которая представляет собой сумму квадратов разностей отклонений теоретической от эмпирической вероятностей безотказной работы трубопровода.

Для размещения расчетных данных выделим ячейки для целевой функции K3 и интенсивности отказов J3. Пример размещения диапазонов исходных и расчетных данных приводится на рис. 4.1.

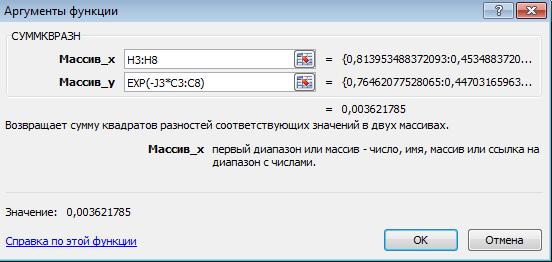
Рис. 4.1. Пример размещения диапазонов исходных и расчётных данных

Вычисление суммы квадратов разностей при начальном значении λ = 0 осуществим с помощью стандартной функции СУММКВРАЗН. С помощью цепочки команд ≪Формулы => Вставить функцию≫ вызовем диалоговое окно мастера функций, в котором выберем функцию СУММКВРАЗН. Из списка предложенных функций выберем функцию СУММКВРАЗН, в результате чего откроется диалоговое окно данной функции с двумя аргументами, приводимое на рис. 4.2. В качестве массива X запишем диапазон адресов ячеек H3-H8, в которых находятся значения эмпирических вероятностей безотказной работы трубопровода P_сi(t). В качестве массива Y запишем формулу расчета значений теоретической функции надежности (t) , которая примет следующий вид: = ЕХР(-J3*H3: H8).

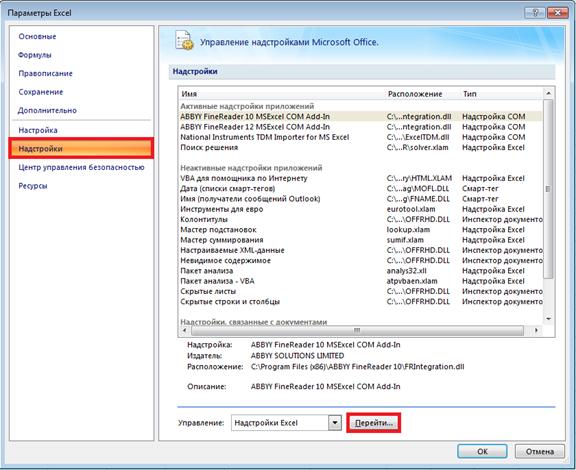
Рис 4.2 Диалоговое окно стандартной функции СУММКВРАЗН

Где J3 — адрес ячейки, в которой хранится значение интенсивности отказов, в данном случае оно равно нулю; С3:С8 — диапазон ячеек, содержащих значения времени t.

В итоге в ячейке K3 получим следующую формулу для вычисления целевой функции Z:

= СУММКВРАЗН(H3:H8;ЕХР(-J3*C3:C8))

Нажав клавишу ≪ОК≫, получим значение целевой функции Z  при λ= 0 в ячейке J3.

Этап 3. С помощью метода ≪Поиск решения≫ определяется значение коэффициента интенсивности отказов λ, при котором сумма квадратов разностей Z будет минимальной.

Для этого потребуется открыть параметры Microsoft Excel 2007 и подключить метод «Поиск решения» рис 4.3, рис 4.4.

Рис 4.3 Активация метода «Поиск решения» в Microsoft Excel 2007

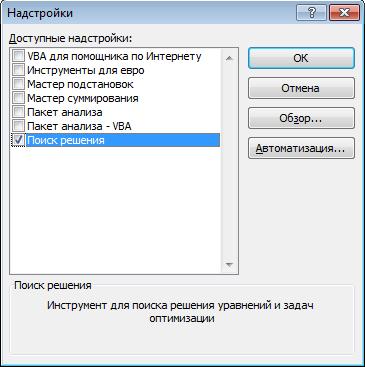
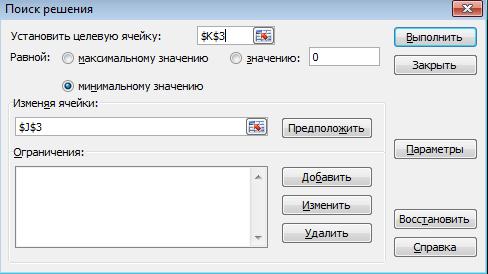
Рис 4.4 Доступные надстройки Excel

Рассмотрим описание полей диалогового окна ≪Поиск решения≫. Установить целевую ячейку — задается ссылка на целевую функцию, которая минимизируется, либо максимизируется, либо строго приравнивается конкретному значению.

Группа ≪Равной≫— переключатель устанавливается на любой из трех следующих вариантов:

1. Максимальному значению — ищется максимальный результат для целевой ячейки.

2. Минимальному значению — ищется минимальный результат для целевой ячейки.

3. Значению — находятся точные значения для изменяемых ячеек так, что величина в целевой ячейке равна выделенной здесь величине.

Изменяя ячейки — указывается ячейка или смежные ячейки, которые должны изменяться в процессе поиска наилучшего решения. Кнопки ≪Добавить≫, ≪Изменить≫, ≪Удалить≫ — позволяют ввести и работать с ограничениями в специальном диалоговом окне. Выполнить — осуществляет поиск наилучшего решения. Чтобы прервать слишком затянувшийся процесс поиска решения следует нажать клавишу <Esc>.

Заполним открывшееся диалоговое окно ≪Поиск решения≫, как показано на рис. 4.5, установив следующие значения: - для целевой ячейки укажем адрес  K3, где находится значение целевой функции Z; - переключатель для целевой функции установим в положение равное ≪минимальному значению≫; - в поле ≪изменяя ячейки≫ укажем адрес ячейки J3, где находится значение интенсивности отказов. Здесь указываются ячейки, которые должны изменяться в процессе поиска решения задачи, т. е. ячейки, отведенные под переменные задачи. Ограничения в нашем случае отсутствуют, поэтому данное поле мы не заполняем. Теперь следует нажать кнопку ≪Параметры≫ в диалоговом окне ≪Поиск решения≫ (рис. 4.5), для того чтобы проверить, какие параметры заданы для поиска решений. В открывшемся окне, образ которого приводится на рис. 4.6, можно изменять условия и варианты поиска решений исследуемой задачи, а также загружать и сохранять оптимизируемые модели.

Рис 4.5 Диалоговое окно метода «Поиск решений»

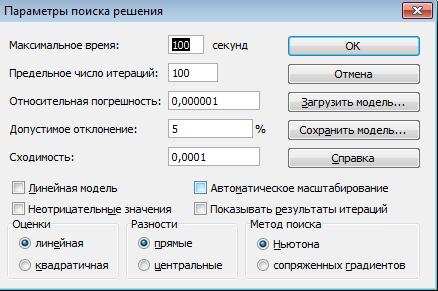
Рис 4.6 Диалоговое окно параметров метода «Поиск решения»

Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач и для нашего случая тоже, поэтому ничего менять не будем. Нажмем кнопку ≪ОК≫, чтобы выйти из среды диалогового окна ≪Параметры поиска решения≫ и кнопку ≪Выполнить≫, чтобы выйти из среды диалогового окна ≪Поиск решения≫. После команды на выполнение поиска оптимального значения интенсивности отказа появится диалоговое окно «Результаты поиска решения». Для сохранения результата нужно выбрать «Сохранить найденное решение» и указать ячейку значения интенсивности отказа J3.

Получили новое значение целевой функции (суммы квадратов разностей), при новом значении интенсивности отказа.

Таким образом, в результате компьютерного моделирования на основании использования метода наименьших квадратов мы определили теоретическую функцию надежности трубопровода (построили модель надежности) ≪без коэффициента≫ (С = 1), имеющую вид:

P_T(t)=e^-λt

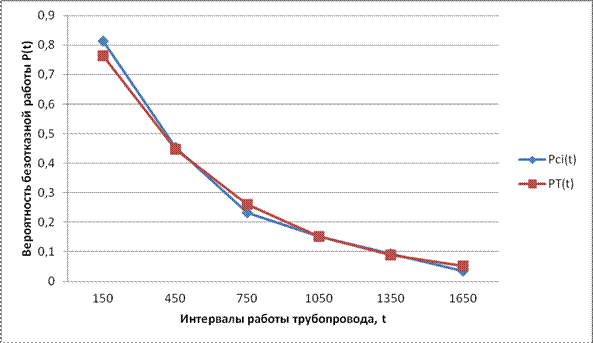
На основании экспериментальных и теоретических данных построим графики функций P_сi(t) и P_T(t). Как видно на рис. 4.7 графики теоретической и экспериментальной моделей находятся близко друг от друга.

Рис 4.7 График сравнения эмпирических и теоретических значений вероятности безотказной работы

Аналогично следует повторить поиск теоретической модели P_2T(t) с коэффициентом С. Для поиска параметра Z задать интенсивность отказов λ₂ и коэффициент С равными 0.

Оформление отчета

    Отчет должен содержать:

1. Титульный лист с названием работы.

2. Цель и задачи работы.

3. Конспект теоретической части и метода построения модели надёжности.

4. Расчетные формулы и расчет всех величин.

5. График рассмотренных режимов.

6. Выводы.

Контрольные вопросы

1. Определение надёжности.

2. Какие эмпирические показатели надёжности использовались в работе, объяснить их назначение.

3. Какая теоретическая модель использовалась в работе, объяснить принцип действия данной модели.

4. Что такое аппроксимация?

5. Какие функции среды Microsoft Excel использовались в работе, объяснить их назначение.