
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Описание метода экспоненциальной регрессииДостаточно много статистических моделей описывается экспоненциальным законом распределения случайной величины, поэтому в Excel разработан специальный метод для построения и анализа подобных моделей — с помощью статистической функции ЛГРФПРИБЛ. Функция ЛГРФПРИБЛ вычисляет коэффициенты экспоненциальной кривой, которая наилучшим образом аппроксимирует имеющиеся данные, а также выдает дополнительную регрессионную статистику. Функция возвращает массивзначений, который описывает полученную кривую. Поскольку данная функция возвращает массив значений, она должна вводиться как формула массива. y = b ∙ mx или y = (b ∙ (m1x1) ∙ (m2x2) ∙...) (в случае нескольких переменных x1, х2, ...), Синтаксис функции: ЛГРФПРИБЛ(известные_y; [известные_x]; [константа]; [статистика]) Известные_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y=b ∙ mx. Известные_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y=b ∙ mx. Если аргумент известные_x опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и известные_y. Константа. Необязательный аргумент. Логическое значение. Если аргумент Константа = 0, то b принудительно полагается равным единице, т.е. y=mx. Если аргумент Константа имеет значение ИСТИНА или опущен, то b вычисляется обычным образом. Статистика. Необязательный аргумент. Логическое значение. Если аргумент Статистика = 0 или опущен, то вычисляются только коэффициенты m и b, а если = 1, то выдаётся ещё и дополнительная статистика по регрессии. Экспоненциальная модель надёжности описывается уравнением (2.17):  Y = C ∙ mx (2.17) В нашем случае неизвестной зависимой величине Y соответствует РТ(t),а величине хсоответствует t. Параметр т определяется формулой (2.18): m = e-λ (2.18) Поэтому искомый параметр — интенсивность потока отказов определяется соответствующим выражением (2.19) через натуральный логарифм: λ = -ln(m) (2.19) Отсюда происходит название функции ЛГРФПРИБЛ — ≪логарифм приближенный≫. Данный метод позволяет получить полную статистику экспоненциальной регрессии.
2.4 Описание выбора оптимального метода моделирования и модели надежности магистрального трубопровода на базе корреляционного анализа в Microsoft Excel 2007 При оценке надежности технических систем одной из важных задач является исследование стохастической (вероятностной) зависимости между изучаемыми переменными. Зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого. Для количественной оценки связи между изучаемыми переменными используются показатели корреляции. Линейный коэффициент корреляции характеризует степень зависимости между двумя коррелируемыми признаками. Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон. Коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Если же связь между переменными X и Y не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение. Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях. Знак коэффициента корреляции очень важен для интерпретации полученной связи. Подчеркнем еще раз, что если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости. Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. В общем виде формула для подсчета коэффициента корреляции такова:
где Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать или убывать по линейному закону. Если две исследуемые случайные величины X и Y связаны точной линейной функциональной зависимостью, то коэффициент корреляции равен ±1, т. е. RXY = ±1. Знак «минус» означает, что при возрастании одной случайной величины другая убывает. В общем случае, когда случайные величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции RXY принимает значение в пределах от 1 до -1 (-1 < Rn < 1). Тогда оценка корреляции случайных величин может быть определена по шкале Чеддока, приводимой в таблице 1 в зависимости от значения коэффициента корреляции RXY. Таким образом, по значению коэффициента корреляции можно проверить соответствие построенных теоретических моделей статистическим моделям. Комплекс методов статистической обработки данных, представленный в виде пунктов меню «Анализ данных» в Excel, позволяет проводить анализ статистических данных. Каждый метод реализован в виде отдельного режима работы. Таблица 2.2 Шкала Чеддока
Достоверность построенных моделей надежности трубопровода проверяется с помощью метода «Корреляция». |
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 462. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||
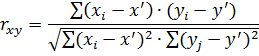
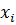 - значения, принимаемые в выборке Х,
- значения, принимаемые в выборке Х, 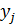 - значения, принимаемые в выборке Y;
- значения, принимаемые в выборке Y; 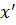 - средняя по Х,
- средняя по Х, 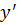 - средняя по Y.
- средняя по Y.