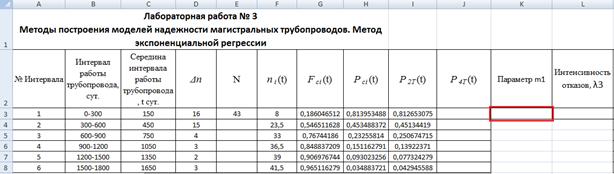
Лабораторная работа №3. Методы построения моделей надежности магистральных трубопроводов. Метод экспоненциальной регрессии

Далее следует выделить свободную колонку под ожидаемый результат электронной таблицы в Excel размером 5х1, содержащей ячейки I3-I8.

Значения параметров С и m экспоненциальной регрессии (см. формулы 1, 2) определяются с помощью статистической функции ЛГРФПРИБЛ.

Подготовив на листе ячейки (рис.4.15), выделим ячейку параметра m K3.

Рис. 4.15 Рассчитанные исходные данные и выделенные ячейки для ожидаемого результата

После выделения ячейки параметра m, следует открыть вкладку ≪Формулы≫, затем ≪Вставить функцию≫. В открывшемся диалоговом окне ≪Мастер функций≫ выбрать функцию ЛГРФПРИБЛ (рис.4.16, рис. 4.17).

Рис. 4.16 Вставка функции в ячейку параметра m

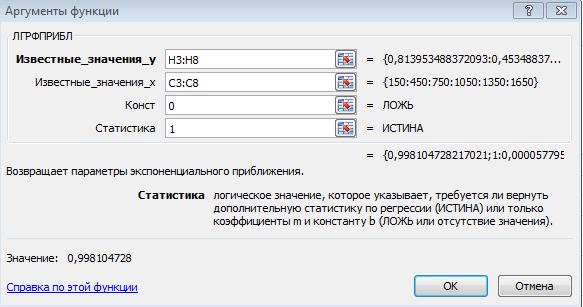
Рис. 4.17 Выбор функции ЛГФПРИБЛ в диалоговом окне ≪Мастер функций≫

Функция имеет четыре аргумента, которые представлены на рис. 4.18, заполним их данными.

1. Известные значенияу— массив известных значений зависимой наблюдаемой величины. В поле первого параметра введем адреса ячеек H3-H8, в которых находятся значения эмпирических вероятностей безотказной работы магистрального трубопровода P_ci(t).

2. Известные значениях— массив известных значений независимой наблюдаемой величины. В поле второго параметра введем адреса ячеек C3-C8, в которых находятся значения середины временного интервала t.

3. Конст— логическое значение, которое указывает на наличие в формуле (1) коэффициента С.

Если данный аргумент имеет значение ИСТИНА, что соответствует наличию значения ≪1≫ в диалоговом окне аргумента. Если аргумент Констимеет значение ЛОЖЬ, что соответствует наличию значения ≪0≫ в диалоговом окне аргумента, то коэффициент С ≪отсутствует≫, т. е. не вычисляется (С = 1).

В поле третьего параметра введем значения ≪0≫, т.е. построим модель надежности трубопровода ≪без коэффициента≫. Соответственно, для расчёта экспоненциальной регрессии для функции Р_2Т, имеющую коэффициент С в поле третьего параметра следует вводить значение ≪1≫.

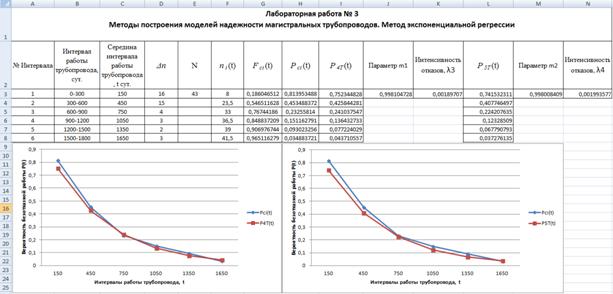
Рис. 4.18 Аргументы функции ЛГРФПРИБЛ

В результате всех проведённых расчётов должны быть получены теоретические значения обработки по методу экспоненциальной регрессии эмпирических данных Р_4Т(t) и теоретических данных с коэффициентом С - Р_5Т (t). Так же должны быть построены сравнительные графики для найденных величин (рис. 4.19).

Рис. 4.19 Окно выполненной лабораторной работы на третьем листе Microsoft Excel 2007