
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Описание метода наименьших квадратовСуть данного метода заключается в том, чтобы для некоторого набора эмпирических дискретных значений (x1,y1) при i = 1, ..., п подобрать такую теоретическую функцию y1= f(x), значения которой ≪наилучшим образом≫ приближались бы к y1 при заданных x1. В качестве критерия точности приближения, что соответствует понятию ≪наилучшим образом≫, используется минимум суммы квадратов разностей отклонений теоретической функции от эмпирических значений. В итоге задача аппроксимации (научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми) сводится к задаче оптимизации, т. е. ищутся такие коэффициенты теоретической функции, при которых сумма квадратов разностей отклонений теоретической функции от эмпирических значений была бы минимальна. Проиллюстрируем практическое использование данного метода на реальном примере определения функции надежности (построения модели надежности) линейной части трубопровода по данным обработки статистической информации об отказах. Сначала, используя исходные данные, следует подсчитать число (частоту) значений случайной величины в каждом интервале (например, число отказов в интервале исследуемого объекта ТС)– эмпирическую частоту отказов в интервале Δn и число отказов к моменту ni(t) (суммарное число отказов в текущем интервале, вычисленное для середины интервала). ni (t)=a1+a2+…+ai /2, (2.1) где a1…an значения эмпирической частоты отказа в интервалах (Δn); ai значение эмпирической частоты в текущем интервале. Следовательно, для первого интервала формула примет вид:  ni (t)=ai /2 (2.2) Далее следует определить эмпирическую вероятность отказов для середины интервала
где Исходя из положения, что полная группа событий равна 1, т.е.
Полученные данные представить в виде таблицы в среде Excel. В результате обработки статистических данных по отказам линейной части магистрального трубопровода получено эмпирическое распределение времени безотказной работы магистрального трубопровода, которое приводится в табл. 1.3. Необходимо определить теоретическую функцию надежности для данного трубопровода на основании эмпирических данных, приводимых в таблице. Для решения поставленной задачи на первом этапе необходимо выдвинуть гипотезу о типе теоретической функции надежности (экспоненциальный, Вейбулла, Пуассона и т. п.). Воспользуемся накопленным практическим опытом в области построения функций надежности объектов трубопроводов. Известно, что надежность линейной части трубопровода хорошо описывается экспоненциальным законом. Поэтому выдвигаем гипотезу, что теоретическая функция надежности имеет экспоненциальную зависимость вероятности от времени безотказной работ трубопровода. Табл. 2.1. Дискретные эмпирические значения распределения времени безотказной работы магистрального трубопровода
Однако экспоненциальная функция надежности может принимать один из двух следующих видов (без коэффициента и с коэффициентом): PT (t) = е-λt (2.5) P2T (t) = C е-λt (2.6) где PT (t), P2T (t) — вероятность безотказной работы трубопровода; t— время; λ — интенсивность отказов; С — коэффициент. Остановимся на более простом выражении (5), где функция надежности представляется без коэффициента. Целью является аппроксимировать эмпирические (статистические) дискретные данные Pci экспоненциальной кривой, теоретические значения которой PT в заданных точках ti , максимально совпадали бы с эмпирическими данными. Это означает, что нужно минимизировать отклонения теоретических значений PT от эмпирических значений Pci вероятности при заданных значениях времени ti , что наглядно можно видеть на рис. 1.1. Отклонения теоретических значений PT от эмпирических Pci могут быть как со знаком «плюс», так и со знаком «минус», поэтому вычисляют квадрат отклонений (Pci (t) - (PT (t))2 чтобы избежать негативного влияния знака «минус» на результат вычислений). Эмпирические значения вероятностей Pci (t) и значение времени t представлены в табл. 1.3, а теоретические значения вероятностей (PT (ti) согласно выдвинутой гипотезе можно вычислить по формуле (5). Для учета всех отклонений при заданных шести значениях t следует вычислить сумму квадратов разности отклонений Z, которая в данном случае будет определяться формулой:
Таким образом, мы определили целевую функцию Z, для которой неизвестным параметром является интенсивность отказов λ.
Рис 1.1 Графическое представление метода наименьших квадратов В итоге задача сводится к поиску оптимального значения интенсивности отказов λ, при котором целевая функция стремится к минимуму. Поэтому формулу (7) можно представить в ином виде (8): Для решения задач оптимизации в Excel есть специальный метод ≪Поиск решения≫. |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 502. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
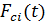 по следующей формуле:
по следующей формуле: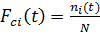 (2.3)
(2.3)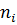 (t) – число отказов к моменту (суммарное число отказов в текущем интервале, вычисленное для середины интервала); i – номер интервала; N – суммарное количество всех наблюдений (число отказов за весь период наблюдения).
(t) – число отказов к моменту (суммарное число отказов в текущем интервале, вычисленное для середины интервала); i – номер интервала; N – суммарное количество всех наблюдений (число отказов за весь период наблюдения).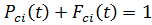 , определяется распределение эмпирической функции надежности
, определяется распределение эмпирической функции надежности 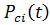 , таким образом, вычисляется ее значение на каждом интервале:
, таким образом, вычисляется ее значение на каждом интервале: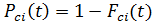 (2.4)
(2.4)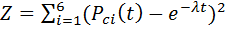 (2.7)
(2.7)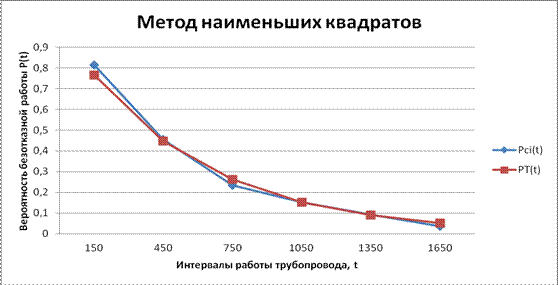
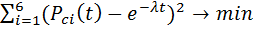 (2.8)
(2.8)