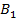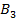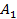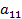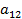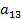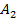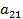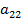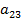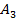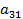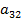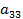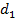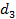Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задач принятия решений в условиях неопределенности1. Нахождение оптимальной стратегии работы транспортного предприятия в условиях неопределенности при помощи критерия Сэвиджа. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений:
Необходимо выбрать оптимальную стратегию. (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.) 2. Нахождение оптимальной стратегии работы транспортного предприятия в условиях неопределенности при помощи критерия Гурвица. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений: 
Необходимо выбрать оптимальную стратегию. ( (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.) 3. Нахождение оптимальной стратегии работы транспортного предприятия в условиях неопределенности при помощи критерия Лапласа. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений:
Необходимо выбрать оптимальную стратегию. (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.) 4. Нахождение оптимальной стратегии работы транспортного предприятия в условиях неопределенности при помощи критерия Вальда. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений:
Необходимо выбрать оптимальную стратегию. (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.) 5. Нахождение оптимальной стратегии работы транспортного предприятия в условиях неопределенности. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений:
Необходимо выбрать оптимальную стратегию. (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.) 6. Решение задачи выбора станков для изготовления партии изделий в условиях неопределенности. Один из пяти станков должен быть выбран для изготовления партии изделий, размер которой Q может принимать три значения:
Данные для
Решите задачу для каждого из следующих критериев Лапласа, Вальда, Сэвиджа и Гурвица (положите (Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с: ил.)
Теория игр 1. Аналитическое решение игры
Найти решение игры. (Вентцель Е.С. Введение в исследование операций. Москва: Изд-во «Советское радио», 1964.) 2. Решение тактической задачи вооружения при помощи теории игр. Красные посылают в район расположения Синих два бомбардировщика
Оба бомбардировщика имеют одинаковое вооружение: стрелковые установки одного бомбардировщика сбивают истребитель с вероятностью Задача бомбардировщиков — донести бомбу до цели; задача истребителя — воспрепятствовать этому, т. е. сбить самолет-носитель. Требуется выбрать оптимальные стратегии сторон, а именно: для Красных: — какой бомбардировщик сделать носителем? для Синих: — какой бомбардировщик атаковать? (Вентцель Е.С. Введение в исследование операций. Москва: Изд-во «Советское радио», 1964.) 3. Решение задачи нахождения стратегий спортивных клубов при помощи метода итераций.Спортивный клуб А располагает тремя вариантами состава команды Al, A2 и А3. Клуб В— также тремя вариантами B1, В2 и В3. Подавая заявку для участия в соревновании, ни один из клубов не знает, какой состав изберет противник. Вероятности выигрыша клуба А при различных вариантах составов команд, примерно известные из опыта прошлых встреч, заданы матрицей.
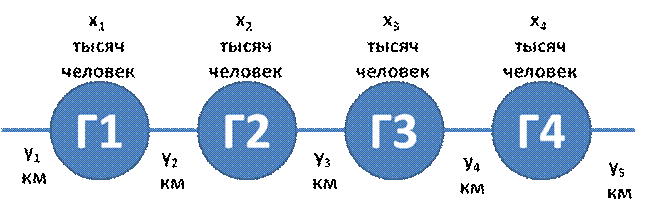
Найти, с какой частотой клубы должны выставлять каждый из составов во встречах друг с другом, чтобы добиться наибольшего в среднем числа побед. Для решения задачи провести n итераций. (Вентцель Е.С. Элементы теории игр. М: Государственное издательство физико-математической литературы, 1961.) 4. Решение задачи нахождения оптимальной стратегии фирм при использовании теории матричных игр. Две конкурирующие крупные торговые фирмы Ф1 и Ф2 планируют построить в одном из четырех городов Г1,Г2, Г3 и Г4, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и численность населения показаны на следующей схеме. Распределение оборота, получаемого каждой фирмой, определяется численностью населения городов, а также степенью удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследование показало, что торговый оборот в универсамах будет распределяться между фирмами так, как это показано в следующей таблице.
Представить описанную ситуацию как игру двух лиц и определить, в каких городах целесообразно фирмам построить свои универсамы. (Афанасьев М.Ю., Багриновский К.А., Матюшок В.М. Прикладные задачи исследования операций: Учеб. пособие. – М.: ИНФРА-М, 2006. – 352 с.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 523. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
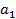 ,
, 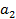 ,
, 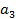 или
или 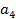 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Ниже приводится таблице, определяющая возможные прогнозируемые затраты на развитие провозных возможностей:
тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Ниже приводится таблице, определяющая возможные прогнозируемые затраты на развитие провозных возможностей: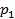
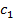
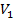
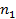
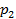
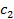
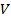
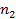
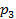
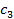
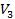
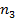
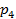
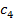
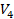
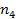
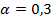 )
)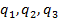 . Производительные затраты
. Производительные затраты 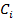 для станка
для станка 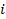 задается следующей формулой:
задается следующей формулой: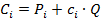 .
.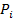 и
и 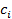 приведены ниже в таблице:
приведены ниже в таблице: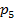
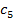
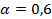 ). Полученные решения сравните.
). Полученные решения сравните.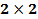 . У «Красных» имеется два вида вооружения
. У «Красных» имеется два вида вооружения 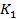 и
и 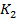 ; у противника («Синие») – два вида помех:
; у противника («Синие») – два вида помех: 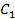 и
и 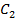 . Вероятность выполнения боевой задачи при различных комбинациях «вооружение» - «помехи» задана матрицей
. Вероятность выполнения боевой задачи при различных комбинациях «вооружение» - «помехи» задана матрицей 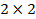 :
: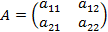 .
.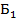 и Б2; Б1 летит впереди, Б2 — сзади. Один из бомбардировщиков — заранее неизвестно какой — должен нести бомбу, другой выполняет функцию сопровождения. По пути к цели бомбардировщики подвергаются нападению истребителя Синих. Если истребитель атакует передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков Б1 и Б2 (Рис. 1). Если он атакует задний бомбардировщик, то по нему ведут огонь только пушки заднего бомбардировщика Б2 (передний не может стрелять, так как в зону обстрела попадает задний бомбардировщик) (рис. 2).
и Б2; Б1 летит впереди, Б2 — сзади. Один из бомбардировщиков — заранее неизвестно какой — должен нести бомбу, другой выполняет функцию сопровождения. По пути к цели бомбардировщики подвергаются нападению истребителя Синих. Если истребитель атакует передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков Б1 и Б2 (Рис. 1). Если он атакует задний бомбардировщик, то по нему ведут огонь только пушки заднего бомбардировщика Б2 (передний не может стрелять, так как в зону обстрела попадает задний бомбардировщик) (рис. 2).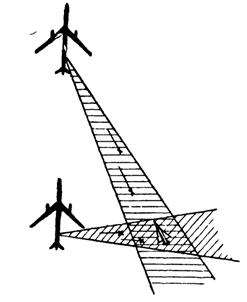 Рис. 1
Рис. 1
 Рис. 2
Рис. 2