Закон убывающей эффективности производства

Этот закон утверждает, что при увеличении одного из основных факторов производства, например, капитальных затрат х, прирост производства начиная с некоторого значения х₀ является убывающей функцией. Иными словами, объем произведенной продукции U как функция от х описывается графиком со сменой выпуклости вниз на выпуклость вверх.

Пример12.2. Пусть зависимость объема произведенной продукции U от капитальных затрат х имеет вид:

U(x) = U₀(1+e^-bx+c)^-1,

где b и с — известные положительные числа (они определяются, прежде всего, структурой организации производства и для нашего частного случая b=3, c=5), а U₀– предельно возможный объем выпускаемой продукции, для нашего частного случаяU₀= 350. Необходимо найти значение х₀, при котором начнет снижаться прирост производства.

Решение.

Аналитическое решение задачи в общем виде выглядит следующим образом. Прирост производства определяется первой производной функции U(x):

.

Скорость изменения прироста определяет ее вторая производная:

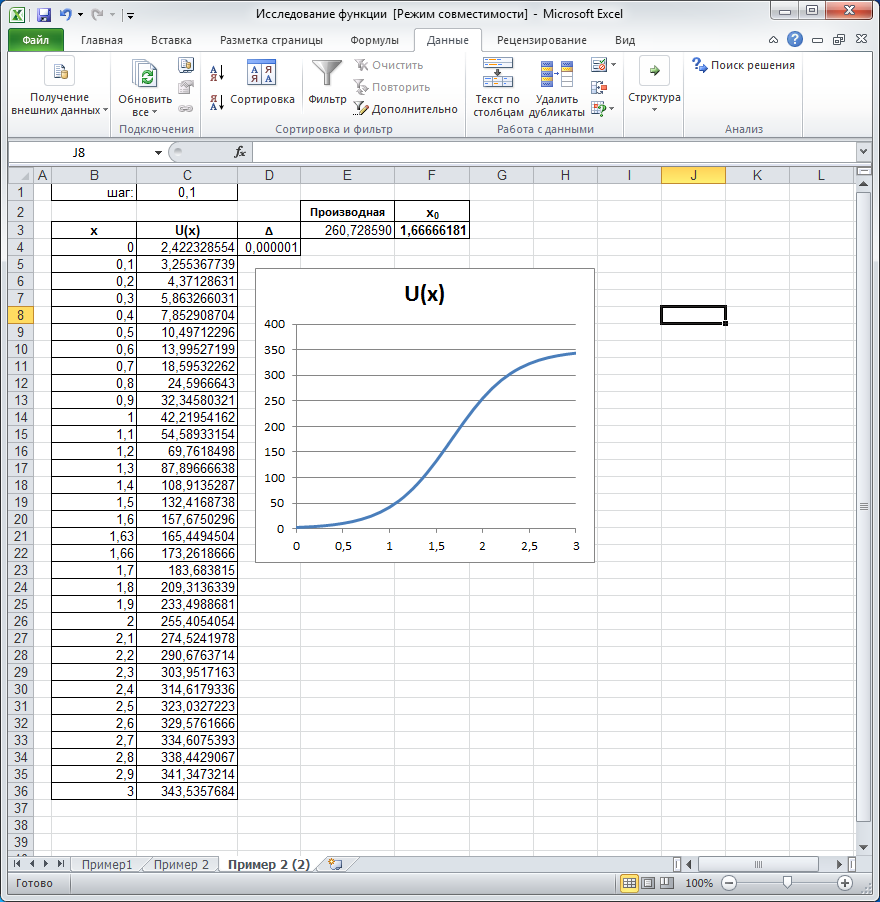
Критическая точка находится из условия: U’’=0Þe^-bx+c – 1Þe^-bx+c= 1Þ -bx + c=0 Þx = c/b, т.е. х₀ = с/b– критическая точка.

Построим таблицу значений аргумента и значений функции. Аргумент х положителен, это капитальные затраты, установим его в интервале от 0 до 3 с шагом 0,1 (определяем опытным путем, проанализировав несколько различных вариантов) и отобразим эту зависимость на точечной диаграмме (рис.79).

Программное вычисление производной и нахождение такого значения х, при котором производная равна 0, приведено на рис. 80. Производная равна 0 в точке х₀= 1,66667. Это критическая точка, которая является либо точкой экстремума, либо точкой перегиба.Полученное значение критической точки х₀ = с/b= 5/3 = 1,66667 совпадает с аналитическим.

Критическая точка находится из условия U’’(x)= 0, однако можно обойтисьбез вычисления второй производной, т.к. аналитически не определили уравнение первой производной. Мы пойдем другим путем. Получим значения производной на выбранном интервале для ее анализа (рис. 81). Производная не меняет знак в окрестности точки х₀, значит это точка перегиба.

Рис. 79. График функции и вычисление производной

Рис. 80. Вычисление максимального значения производной

Рис. 81. Табличные значения производной на отрезке

Добавим также на график точку перегиба функции х₀ и перпендикуляр к оси 0х. В точке перегиба вогнутость графика производственной функции меняется на выпуклость. До этой точки увеличение капитальных затрат хприводит к интенсивному росту объема продукцииU: темп прироста объема продукции (аналог первой производной) возрастает. При х >1,66667 темп прироста объема выпускаемой продукции снижается, и эффективность увеличения капитальных затрат падает.

Предел функции при х® +¥ равен 350 (рис. 82), таким образом, у = U₀ является горизонтальной асимптотой. Добавим ее на график.

Рис. 82. Предел функции на +¥

Таким образом, в стратегии капиталовложений оказывается очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приводить все к меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производства: "улучшать" показатели b, с и U₀ в сторону повышенияэффективности капиталовложений.