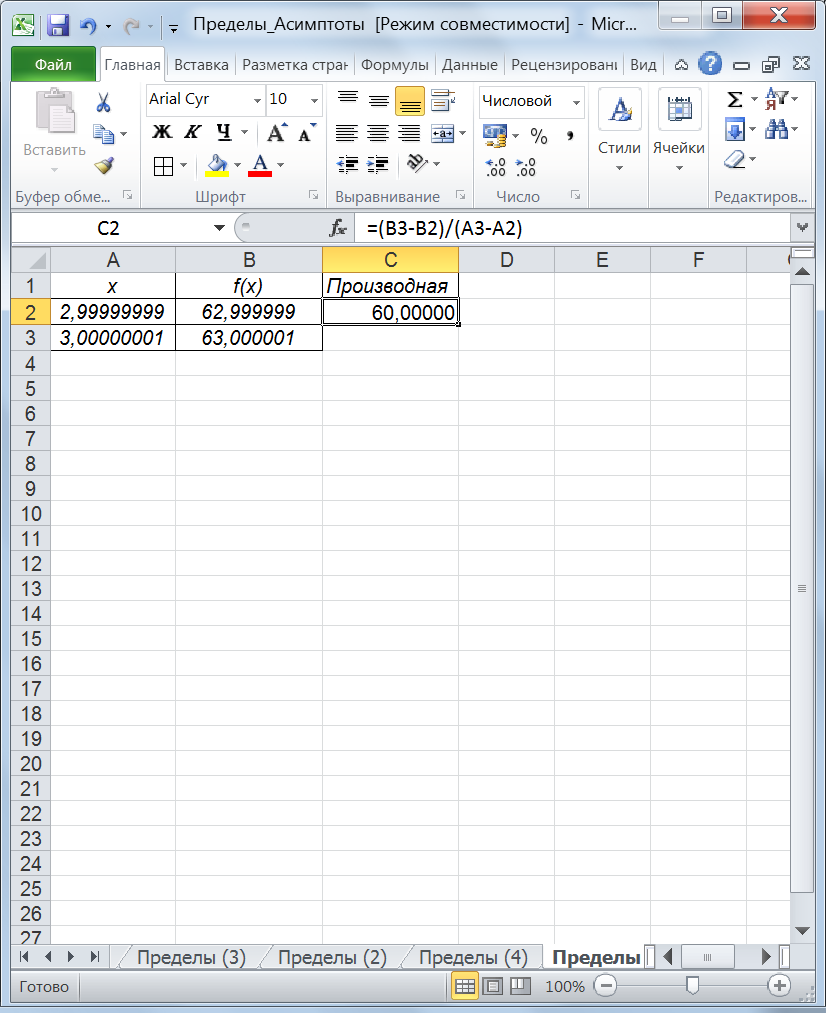
Приближенное вычисление производной функции (2 часа)

Выражение для вычисления производной функцииодного переменной в точке x_k, записанное в конечных разностях, имеет вид:

F’(x_k) = ΔF/Δx = (F(x_k+1) – F(x_k))/(x_k+1 – x_k),

где Δx – очень малая конечная величина.

При достаточно малых значениях Δх, можно с приемлемой точностьюполучить величину производной функции в точке. Для вычисления производной в MS Excel будем использовать приведенную выше формулу. В качестве x_k+1иx_kможно использовать достаточно малую окрестность точки x_k, или в качестве x_kсамо значение x_k, а в качестве x_k+1– достаточно малое приращение аргумента.

Рассмотрим технологию вычисления производной на примерах.

Пример 11.1. Найти производную функции у= 2x³ + x² в точкех=3.

Решение. Вычислим аналитически производную функции в точке х=3: у’ = 3·2·3^2 + 2·3 = 60. Это значение нам понадобится для проверки результата, вычисленного в Excel.

Введем в ячейки А2 и А3(x_k+1иx_k соответственно) значения из окрестности точких=3, достаточно близкие к 3слева исправа, В ячейки В2 и В3 – формулы, соответствующие заданной функции, в ячейку С2 – отношение приращения функции к приращению аргумента (рис. 70).

Рис. 70. Приближенное вычисление производной

В результате выполненных вычислений мы получим результат, совпадающий с аналитическим вычислением производной.

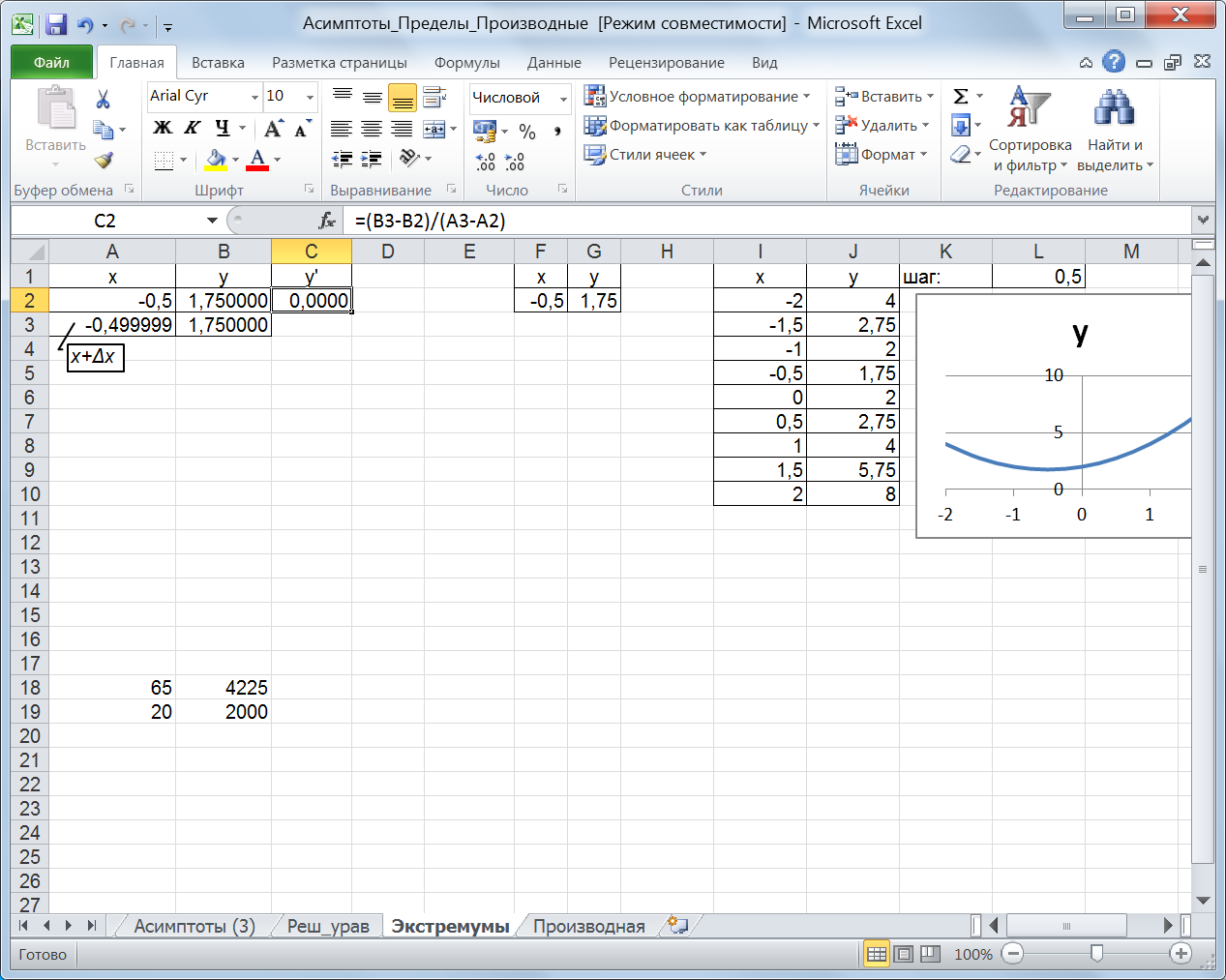
Пример 11.2. Проверим, является ли точка x = -0,5 точкой экстремума функции у= х²+х +2 (пример 10.4).

Решение. Введем в ячейку А3 значение аргумента, а в ячейку А4 достаточно малое приращение аргумента (рис. 71). В ячейки В3 и В4 – значения функции в заданных точках, в ячейке С3 – производную (отношение приращения функции к приращению аргумента). Производная в найденной точке равна нулю, следовательно, найденное ранее значение функции (у=1,75) является ее экстремальным значением.

Рис. 71. Приближенное вычисление производной

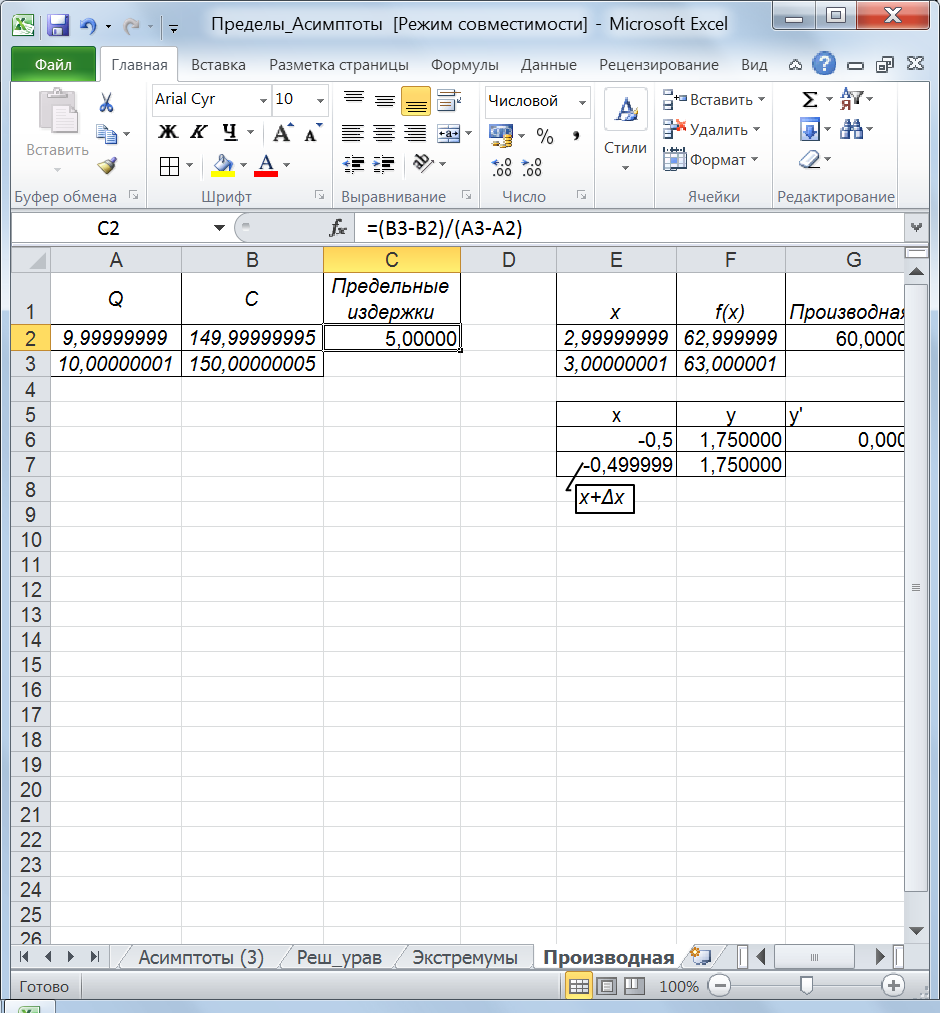
Пример 11.3. Пусть зависимость издержек производства Сот объема выпускаемой продукции в денежных единицах Qвыражается формулой

C=20Q – 0,05Q³.

Требуется определить предельные издержки производства при объеме выпускаемой продукции 10ден.ед.

Решение.В ячейках А2 и А3 поместим значения для левой и правой окрестности аргументаQ. В ячейкуВ2 – формулу =20*A2-0,05*A2^3и скопируем ее в В3.

В ячейку С2 введем формулу вычисления производной =(B3-B2)/(A3-A2). Результат вычислений приведен на рисунке 72.

Рис. 72. Вычисление предельных издержек

Пример 11.4. Зависимость затрат от объема производства задана приведенной ниже таблицей.

Таблица 31.

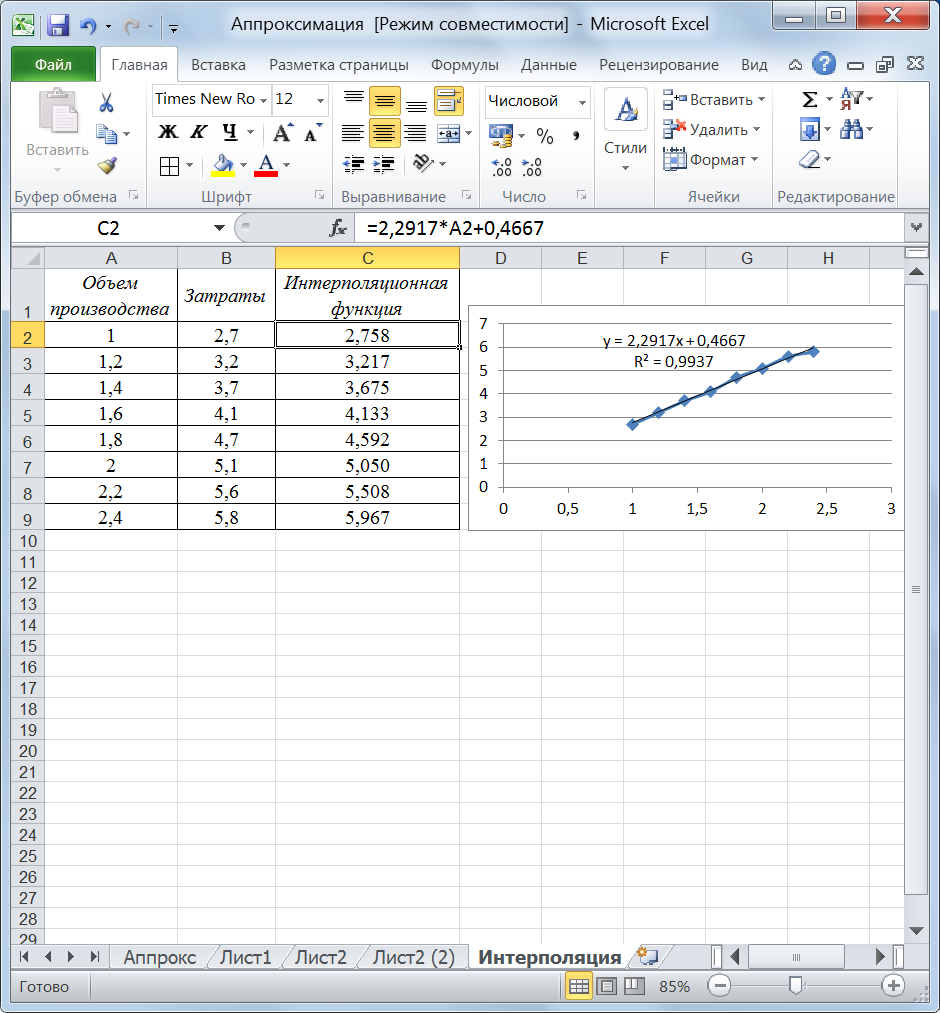
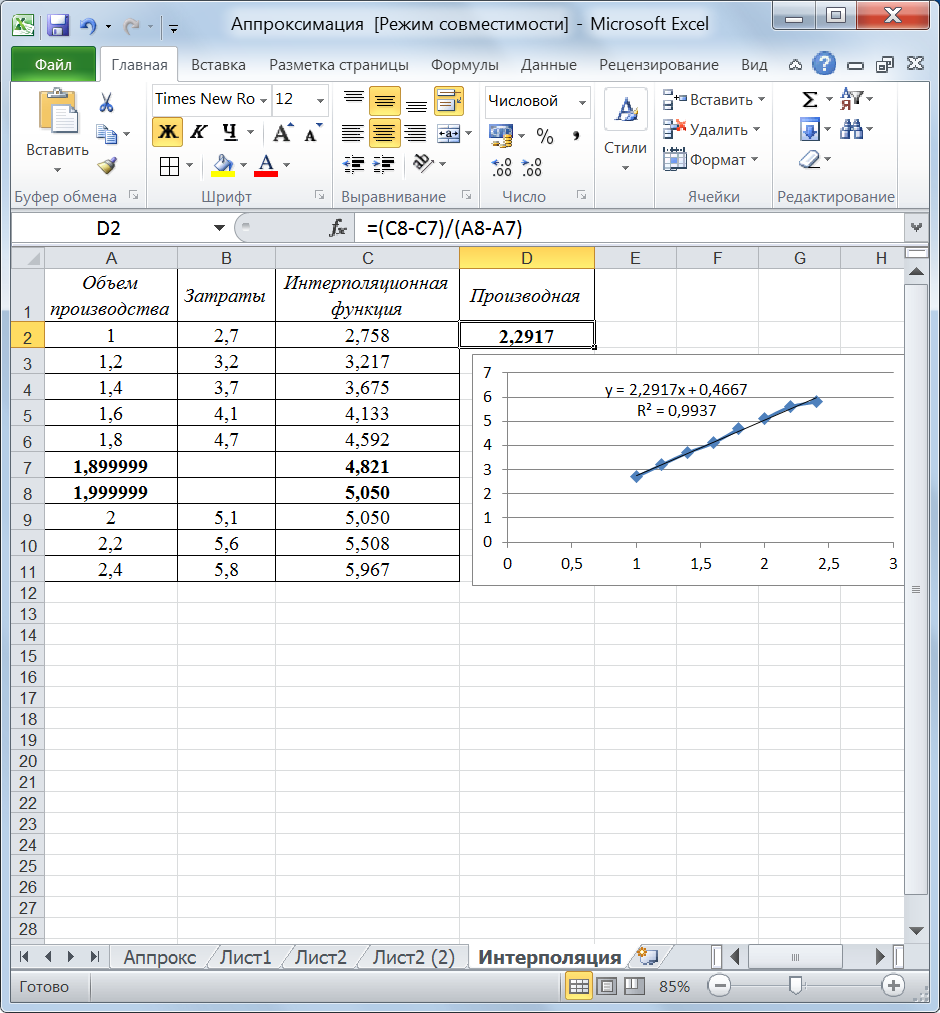
Требуется найти предельные издержки производства при объеме выпуска х=1,9.

Решение. В задаче функция зависимости затрат от объема производства задана не аналитически, а таблично. Поэтому, прежде всего,нужно получить аналитическую зависимость в виде интерполяционной функции и далее использовать ее для решения задачи (рис. 73).

Рис. 73. Аппроксимация табличных значений

Следующим шагом, имея аналитическую зависимость затрат об объема производства, вычислим производную этой функции. Для этого зададим некоторую окрестность точки х=1,9 (можно вставить строчки в таблицу), вычислим значения функции в этих точках и найдем отношение приращения функции к приращению аргумента (рис. 74).

Рис. 74. Решение задачи 11.4