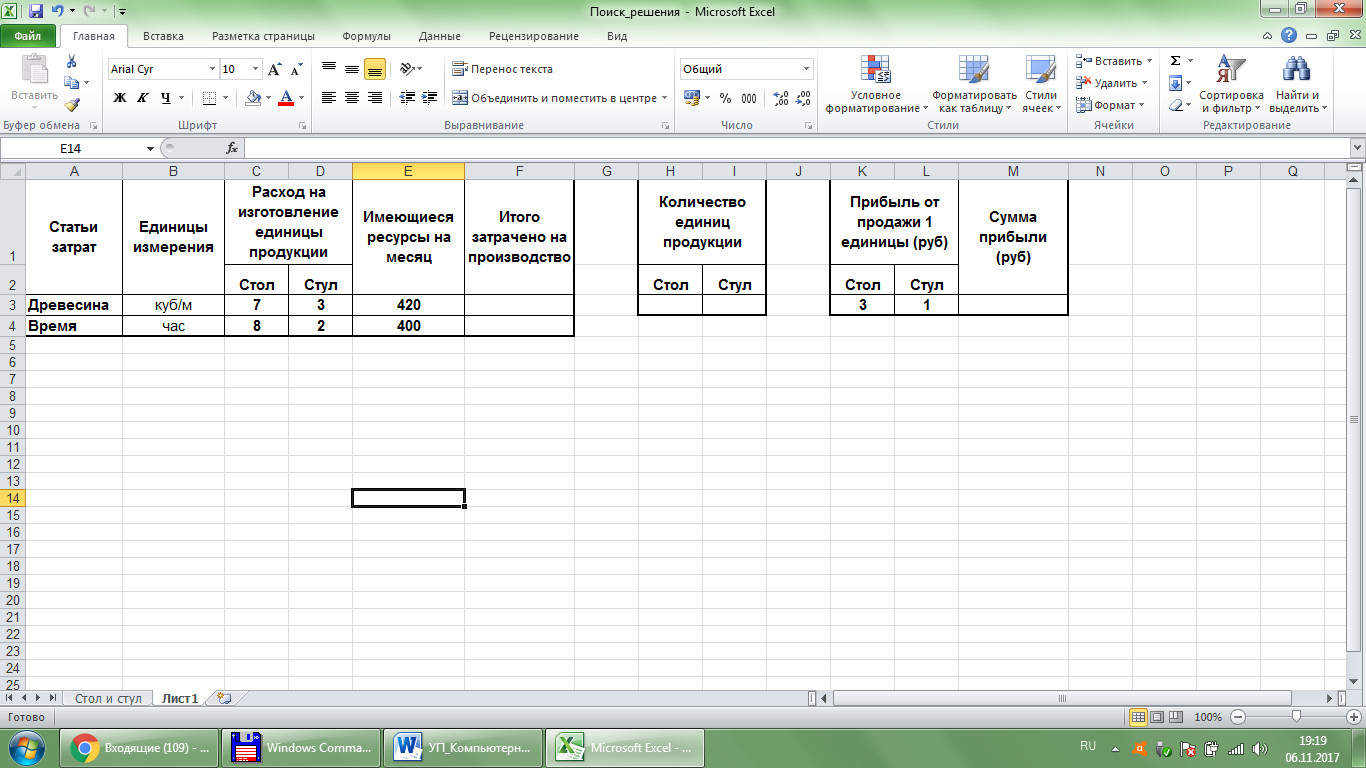
Тема 10. Средство анализа «Поиск решения» (4 часа)

Средство анализа «Поиск решения» является инструментом оптимизации. С помощью этой надстройки Excel можно найти оптимальное или заданное значение некоторой ячейки путем подбора значений нескольких ячеек, удовлетворив нескольким граничным условиям.

Целевая ячейка – это ячейка, для которой нужно найти максимальное, минимальное или заданное значение.

Изменяемые ячейки – это ячейки, от которых зависит значение целевой ячейки. Целевая ячейка должна содержать формулу, прямо или косвенно зависящую от изменяемых ячеек. Поиск решения подбирает значения изменяемых ячеек до тех пор, пока не будет найдено решение.

Ограничение – это условие, накладываемое на некоторую ячейку. Ограничения могут быть наложены на любые ячейки таблицы, включая целевую ячейку и изменяемые ячейки.

Пример 10.1. Фирма производит два вида продукции: столы и стулья.Расход на изготовление единицы продукции дан в виде таблицы (рис. 57). Каждый стул приносит 1 руб. прибыли, а каждый стол – 3 руб. Сколько стульев и столов должна изготовить фирма, если она располагает 420 куб/м древесины и 400 часов рабочего времени и хочет получить максимальную прибыль?

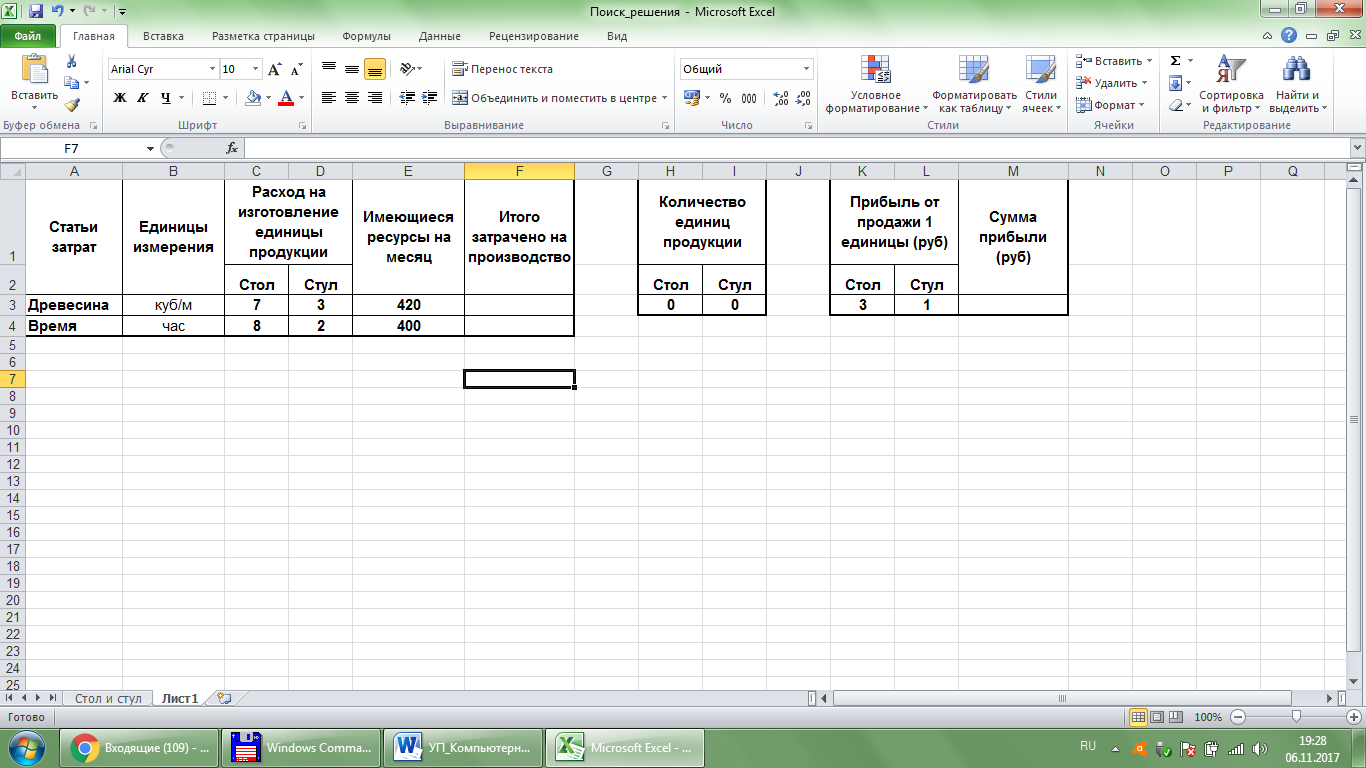
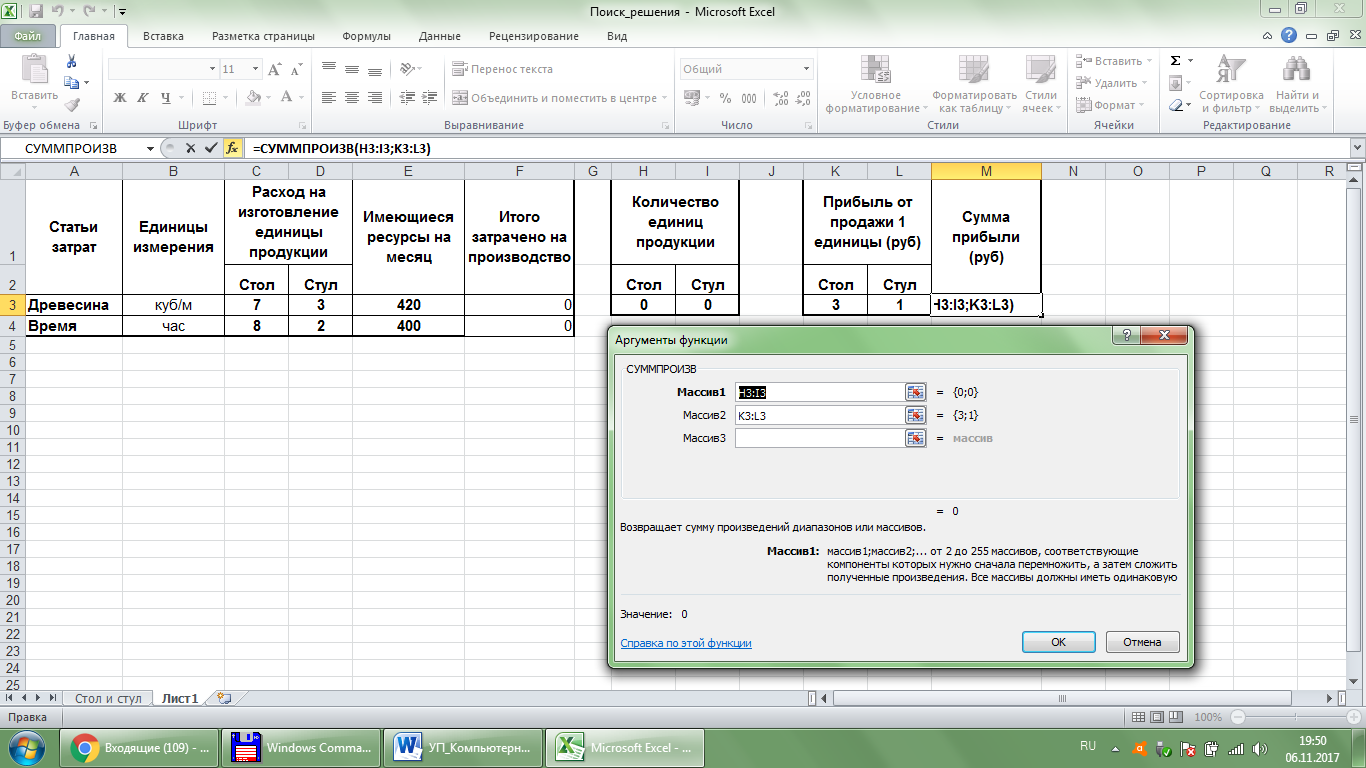
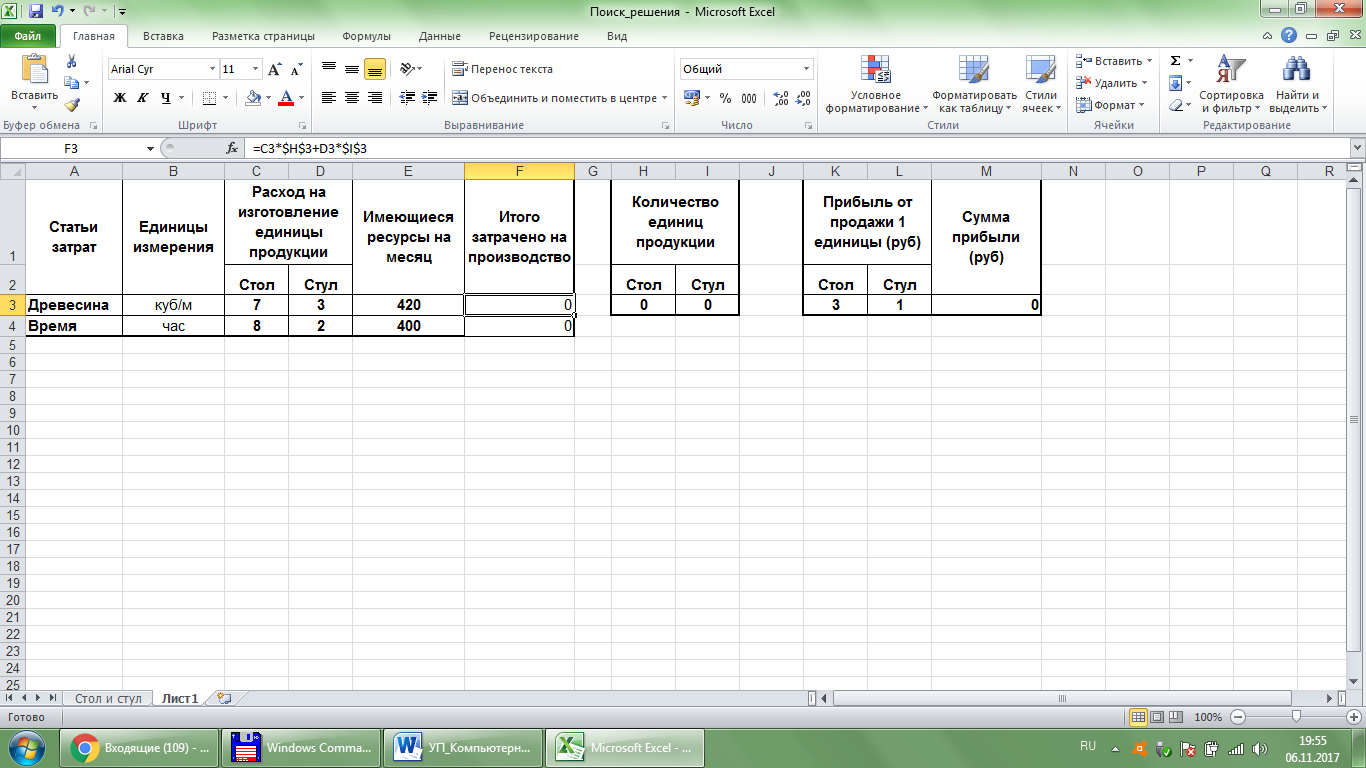
Решение.Определим переменные задачи (рис. 58), от которых будут зависеть величины затраченных ресурсов и будущей прибыли, это количество столов и количество стульев, которые изначально можно установить равными нулю (или 1, или любому другому значению), а далее в этих ячейкахотобразится решение.

Определим целевую ячейку: она должна содержать формулу прибыли от продажи данного количества продукции (СУММПРОИЗВ(Н3:I3;K3:L3)). Будьте внимательны, целевая ячейка и ячейки «Итого затрачено на производство» должны содержать формулы, включающие в себя изменяемые ячейки (рис. 59,60)!

Рис. 58. Переменные задачи

Далее вызовем инструмент «Поиск решения». Обычно он находится на вкладке Данные. Если он у вас отсутствует, необходимо подключить соответствующую надстройку следующими действиями: Файл / Параметры / Надстройки / Поиск решения, нажать кнопку Перейти и снова выбрать Поиск решения.

Рис. 59.Целевая ячейка

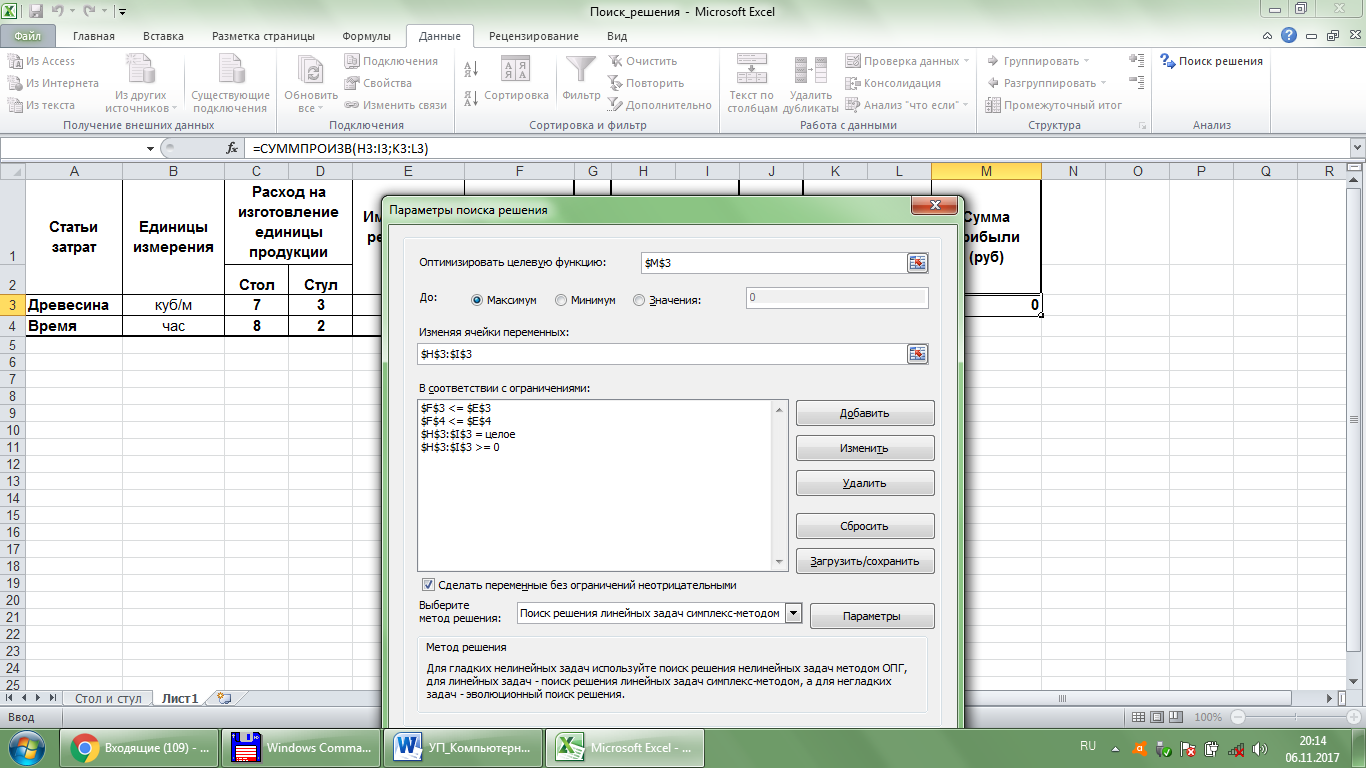
Рис. 60.Ячейки "Итого затрачено на производство"

Заполним окно поиска решениясогласно рисунку 61. Получим решение, представленное на рисунке 62.

Рис. 61.Окно «Поиск решений»

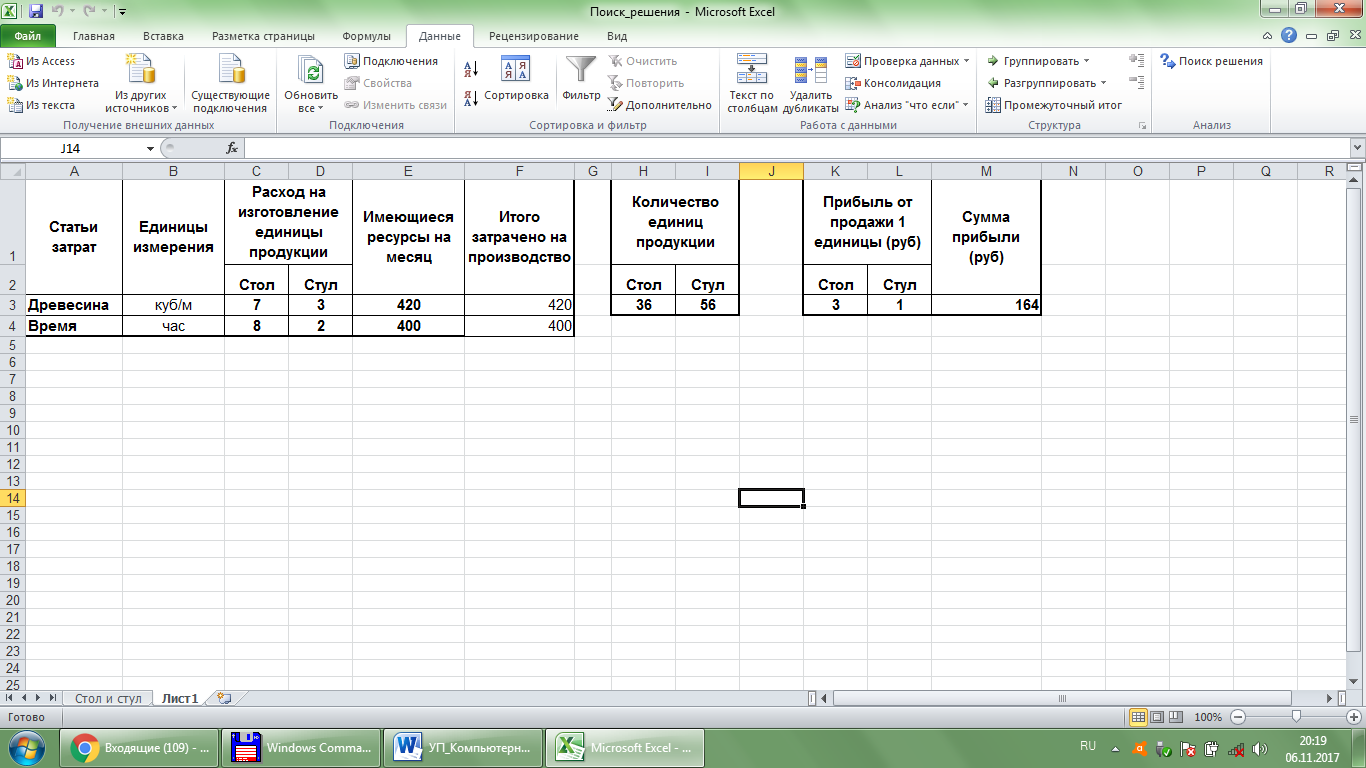
Рис. 62. Решение задачи

Пример 10.2.Фирма «Фасад» производит двери для продажи местным строительным компаниям. Репутация фирмы позволяет ей продавать всю производимую продукцию. Нафирмеработает 10рабочихводнусмену(8 рабочихчасов),5дней в неделю,чтодает 400 часов в неделю.Рабочеевремяподеленомеждудвумя существенноразличнымитехнологическими процессами: собственно производствомиконечнойобработкойдверей.Из400рабочихчасоввнеделю 250отведены под производство и 150под конечную обработку.

«Фасад» производит три типа дверей:стандартные, полированные и резные.В таблицеприведенывременные затратыиприбыльотпродажиоднойдвери каждоготипа.Сколько дверей различных типов нужно производить, чтобы максимизировать прибыль?

Таблица 28.

Решение.Преждевсего,определимцельзадачиивидцелевойфункции.В данномслучае мыхотиммаксимизироватьприбыль,следовательно,целевая функциядолжна вычислять полную прибыль.В задаче заданаприбыль от продажи каждойпроизведенной двери. Поэтомуполнаяприбыль P будет определяться этой прибылью и тем, сколько дверей произведено.

Эти соображения приводят нас к выводу, что в качестве переменных задачи следует выбрать количествадверей каждого типа, которые следует произвести.Значит,взадачебудет3переменных:Х1– количествостандартных дверей,Х2–количествополированныхиХ3–количестворезныхдверей.Целевая функция запишется, очевидно, следующим образом: P = Х1*45+ Х2*90+ Х3*120($).

ЛучшевсегоорганизоватьданныеналистеMSExcelследующимобразом:

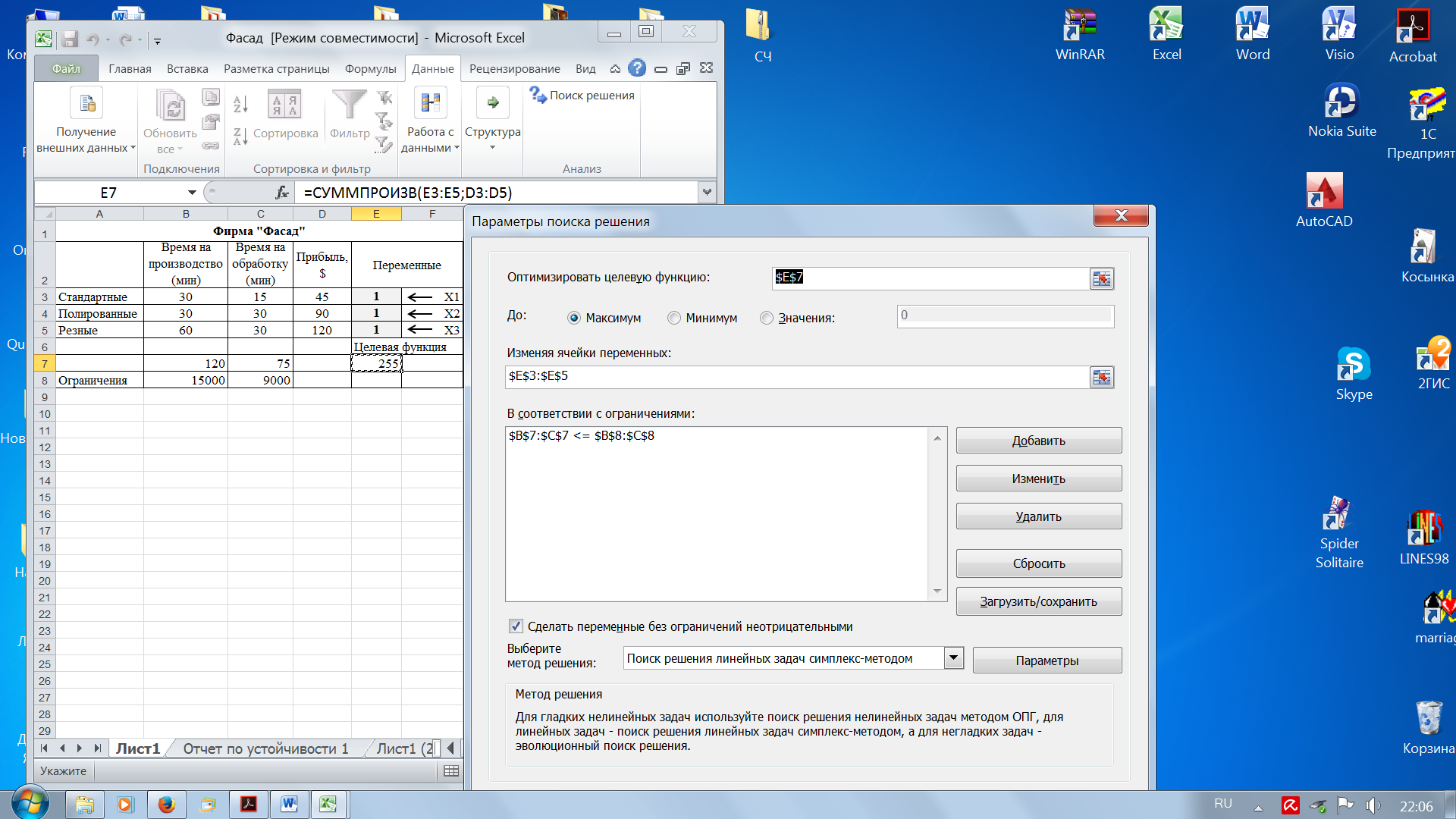
Рис. 63. Исходные данные задачи

Удобновыделить ячейки, в которых будут располагаться переменные цветом, (вданномслучаесерым),и ввести туда любые значения, например, 1, т.к. начальныезначенияпеременных неизвестны, ассылаться напеременные при вычислениях необходимо. Целевая функциязаданас помощьюстандартнойфункции MSExcelСУММПРОИЗВ()(илиSUMPRODUCT()ванглийскойверсии),котораяивычисляет приведенное выше выражение дляP.

Наследующемэтаперешения следует выяснить, при каких ограничениях нужнонайтимаксимальнуюприбыль.Вданномслучаеиз условияследует,что можнозатратитьнапроизводственнуюстадиюнебольше250часоввнеделю,а наобработкунебольше150часов.Других существенныхограниченийвзадаче нет. Итак,следуетподсчитать,сколько временинакаждой стадии потребуется для реализации произвольногопланапроизводства дверей. Для стадии производстваэто время будетравно t1=X1*30+X2*30+X3*60(мин), а для стадии обработки t2=X1*15+X2*30+X3*30(мин), внесем эти формулы в ячейки В7 и С7 соответственно. Поусловию задачи t1<=250*60(мин), аt2<=150*60(мин), добавим эти формулыв ячейки В8 и С8 (рис. 64).

Теперь имеется вся информация, необходимая надстройке «Поиск решения» для определения оптимального по прибыли плана производства (рис. 64).

Рис. 64. Компьютерная модель задачи

Не забудем отметить, чтозадачасоответствует линейноймодели и что переменные неотрицательны. Больше никаких изменений здесь делать не нужно.

ТеперьможнонажиматькнопкуНайти решение,послечегоибудетнайдено решение. Сохраним найденное решение ипроверим,что получилсяследующийрезультат (рис.65).

Рис. 65. Оптимальное решение задачи

Вданномслучаеоказывается,чтомаксимальновозможнаяприбыльравна 33000$и полученаонабудет,еслипроизводитьзанеделю100 полированных дверейи200 резных.Этоиестьоптимальныйплан производства.

Пример 10.3.Сталепрокатныйзаводпроизводитстальныелистытрех различных размеров:100дюймов,80дюймови55дюймов.Поступилзаказнастальные листы размером45, 30 и 18 дюймов в количестве150, 200 и 185 штук соответственно.Какимобразомкомпания должнаразрезать стальныелисты, чтобы минимизировать отходы?

Решение.Этазадачапредставляет своеобразныйтипзадач,вкоторых условие задачи нужнорасшифровать, после чегорешение оказывается очень легким.Вреальнойпрактикеменеджератакиеобстоятельствавстречаютсяочень часто.Чтобыпоставить задачу, нужно перевести формулировкупроблемы на языкколичественныхметодов.

В данной задаче переформулировать условиеоказывается несложно. Из листов каждого из размеров (100, 80 и 55) можно выкроитьпо несколькуразличных наборов заказанныхлистов.Например,излистаразмера55дюймовможнополучить1листразмером45дюймов(10дюймов–вобрезки), или1 листв30дюймов и1в18 дюймов (7–вобрезки),или3листав18дюймов (1 дюйм– вобрезки).Еслиперебратьвсевозможныевариантыраскроя,их окажетсянетак ужмного.Так какдлякаждоговариантаизвестно иколичество полученныхлистов, иколичество обрезков,товыбрав в качестве переменных количестволистов раскроенных по каждомуиз описанныхвариантов, можно построитьзадачулинейнойоптимизации.Целевойфункцией будет общее количествоостатков (сумма произведений (встроенная функция СУММПРОИЗВ()) числа разрезанных листов (диапазон F3:F17) на остаток для каждого типа разрезки (столбец G3:G17)).

Таблица 29.

Цель–минимизация остатковпри условииисполнения заказа.Для проверки условия исполнения заказа необходимо определить полученное количество листов каждого типа как сумму произведения числа разрезанных листов каждого типа (диапазон F3:F17) на количество листов каждого типа для каждого варианта разрезки (диапазон С3:С17 для размера листов в 45 дюймов,диапазон D3:D17 для размера в 30 дюймов,Е3:Е17 для размера в 18 дюймов). Пример организации таблицы для расчета всех нужных для решения задачи величин приведен в таблице 29.

Данные для Поискарешениябудут выглядеть очень просто: целевая ячейка – G19, цель – минимум, изменяемые ячейки – F3:F17.По смыслузадачи следуетпотребовать,чтобы переменныебыли целыми числами (F3:F17 = целое).Как обычно во вкладке параметры отмечаем, что задача линейная ипеременные неотрицательны.

Условиевыполнениязаказаможет бытьзаписанопо-разному. Можно потребовать точноговыполнениязаказа(C18:E18=C19:E19),что,очевидно, соответствует недопустимостиполучениялишних листов заказанных размеров. Можноиспользоватьболеемягкое условие: количествополученныхлистовне менее заказанного (C18:E18>= C19:E19), что допустимо в случае, когда оставшиеся листы могут быть проданы другомузаказчику.

Приответенавопросразумнопотребовать точноговыполнениязаказа. При этомобщее количество остатков будет равняться 675 дюймам. Для выполнения заказа придетсяразрезать44листапо3-емуварианту,3листапо5-омуварианту,106листовпо8-му,44–по10-му и 1 лист по 15-муварианту.