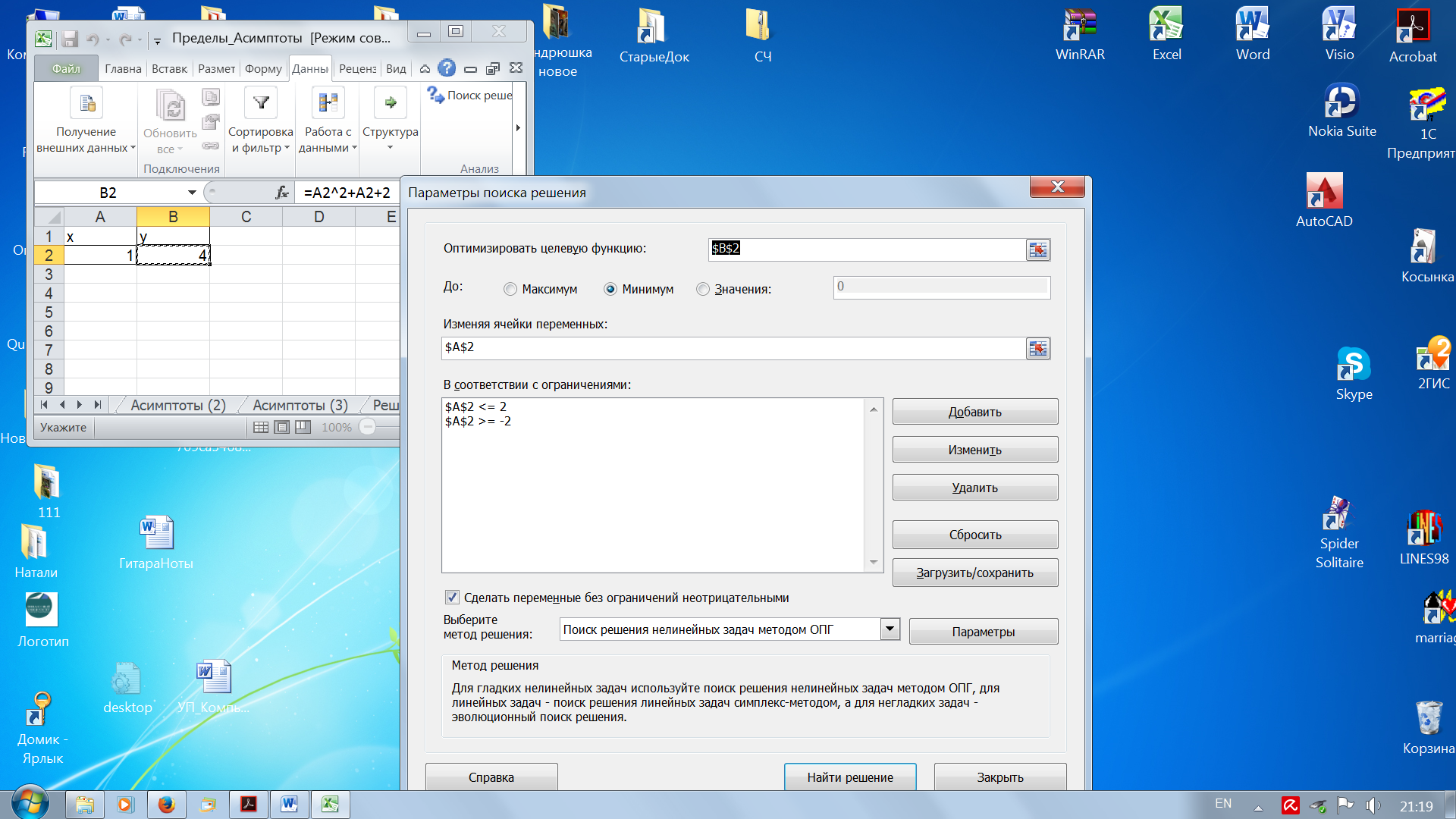
Нахождение локальных экстремумов функции

Если функция F(x) непрерывна на отрезке [a, b] и имеет внутри этогоотрезка локальный экстремум, то его можно найти, используя надстройкуExcel Поиск решения.Рассмотрим последовательность нахождения экстремума функции напримере.

Пример 10.4.Задана неразрывная функция y= x²+ x + 2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2, 2].

Решение. В ячейку А2 рабочего листа введем любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение х (рис. 66).

В ячейку В2 введем формулу, определяющую заданную функциональную зависимость =A2^2 + A2 +2.

Выполним команду меню Сервис Поиск решения.

В открывшемся окне диалога Поиск решенияукажем целевую ячейку (В2), изменяемую ячейку (А2), установим переключатель Минимум, введем ограничения: A2 >= -2 и A2 <= 2. Метод решения в этом случае – Поиск решения нелинейных задач методом ОПГ.

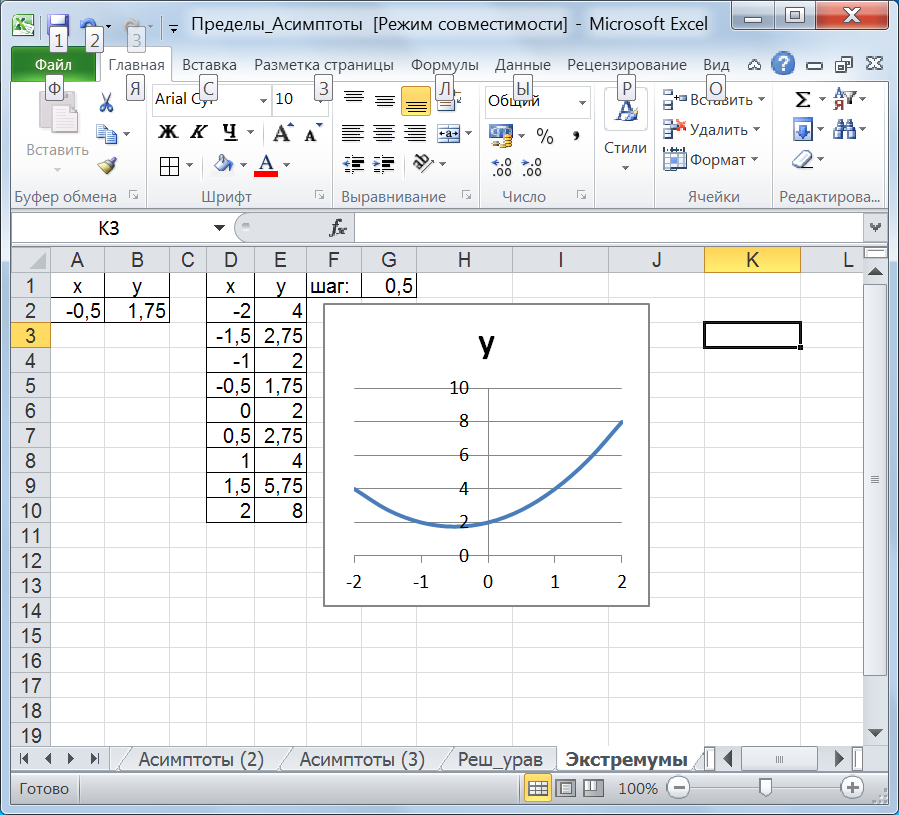
Рис. 66. Компьютерная модель задачи

Щелкнем на кнопке Найти решение. В ячейке А2 будет вычислено значение аргумента х функции, при котором она принимает минимальное значение, а в ячейке В2 – минимальное значение функции.В результате выполнения вычислений в ячейке А2 будет получено значение -0,5переменнойх, при котором функция принимает наименьшее значение в ячейке В2, равное 1,75.

Построим график заданной функции и убедимся, что решение найдено верно (рис. 67).

Рис. 67. Компьютерная модель задачи

Примечание: в частном случае при нахождении локального экстремума с использованием рассмотренной технологии, можно получить значение, которое не является экстремумом, а просто является минимумом или максимумом функциив заданном диапазоне изменения аргумента.Поэтому необходима дополнительная проверка, т.е. вычисление производной функции в найденной точке.Механизм вычисления производной в Excel рассмотрен в следующей главе.