Решение систем нелинейных уравнений

Для решения системы нелинейных уравнений нужно выполнить операции:

1. Выделить рабочие ячейки для неизвестных переменных и ввести в них любые числовые значения переменных из предполагаемой области их определения.

2. В рабочих ячейках записать формулы каждой из функций, составляющих систему в терминах табличного процессора.

3. Включить инструмент Поиск решения. В качестве целевой ячейки указать ячейку, в которой записана формула одной из функций системы. Установить переключатель Значению и в соответствующем поле ввести числовое значение ноль. В поле изменяемых ячеек указать диапазон ячеек, которые определены для вычисления неизвестных переменных. На вычисляемые значения в других ячейках, содержащих формулы оставшихся функций, наложить ограничения на равенство нулю. Выполнить решение.

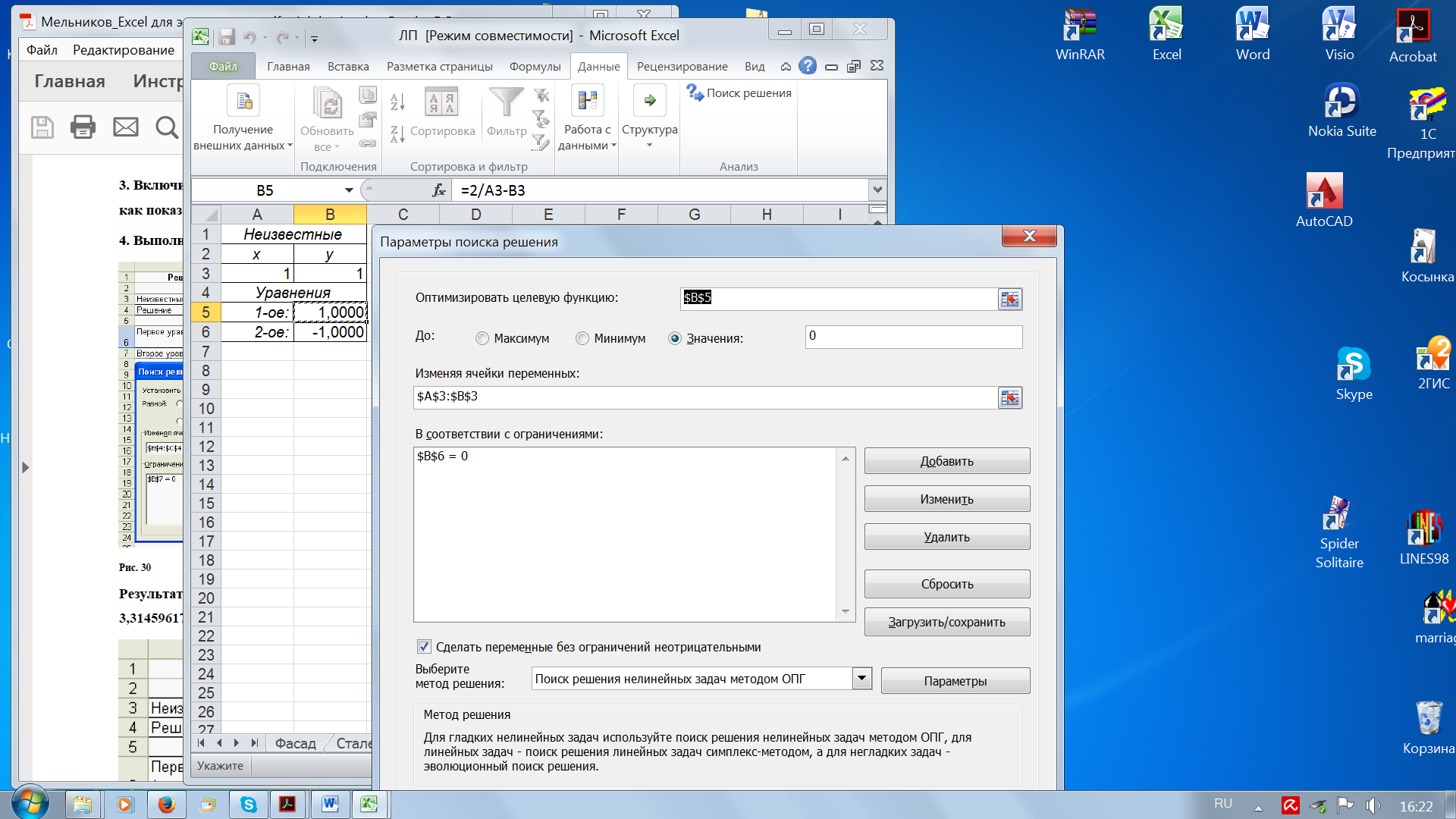
Пример 10.5.Решить систему нелинейных уравнений:

у = 2/х

у² = 2х

на отрезке х ϵ [-2, 2].

Решение. В ячейкиА3и В3рабочего листа введем любые числа из диапазона, например, 1 и 1. В ячейки В5 и В6 – формулы: =2/A3-B3 и =B3^2-2*A3 соответственно (рис. 68). Вызовем Поиск решения. В качестве целевой функции укажем ячейку В5 и установим переключатель Значение равным 0. В качестве изменяемых ячеек укажем ячейки А3 и В3, а в качестве ограничения – равенство 0 второго уравнения, находящегося в ячейке В6. В результате поиска будет найдено решение: х = 1,259921; у = 1,587401.

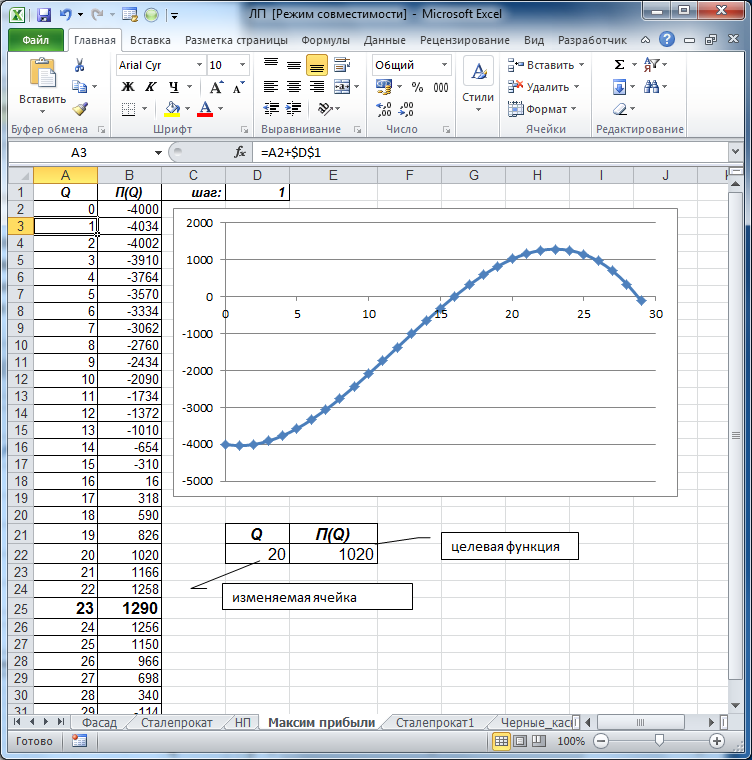
Рис. 68. Решение системы нелинейных уравнений

Максимизация прибыли

Пусть Q – количество реализованного товара, R(Q) – функция дохода; C(Q) – функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой

П(Q) = R(Q) – C(Q).

Пример11.6. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

R(Q) = 100Q – Q²

C(Q) = Q³ – 37Q² + 169Q + 4000.

Решение. Согласно приведенной выше формуле, прибыль П(Q) = -Q³ + 36Q² – 69Q – 4000.

Поскольку количество – величина положительная, построим график функции на отрезке [0; 30] с шагом 1, для чего построим таблицу значений для Qи П(Q) (В2 = –A2^3+36*A2^2–69*A2–4000). Проанализировав внешний вид графика, можно утверждать, что максимум функции находится в окрестности точки со значением х = 20. Введем это значение в изменяемую ячейкуD22, а в ячейку Е22 скопируем формулу вычисления прибыли: = –D22^3+36*D22^2–69*D22–4000(рис. 69).

Рис. 69. Решение системы нелинейных уравнений

Ячейка Е22 содержит целевую функцию, которую необходимо максимизировать. В надстройке Поиск решения укажем ее в качестве целевой ячейки, в качестве изменяемой ячейки укажем ячейкуD22, ограничения в этой задаче отсутствуют. В результате поиска решения получим значение Q = 23, при этомП(Q)=1290, это и есть максимальная прибыль.

Можно проверить решение задачи аналитически: приравнивая производную функции прибыли к нулю, получаем уравнение

C’(Q) = 3Q² – 72Q + 169®-Q²+ 24Q– 23 = 0.

Корни этого уравнения Q₁ = 1, Q₂ = 23, причем при переходе через точкуQ = 23производная меняет знак с плюса на минус. Следовательно, Q = 23 – точка локального максимума, при этом прибыль равна: П_mах = 1290.