Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
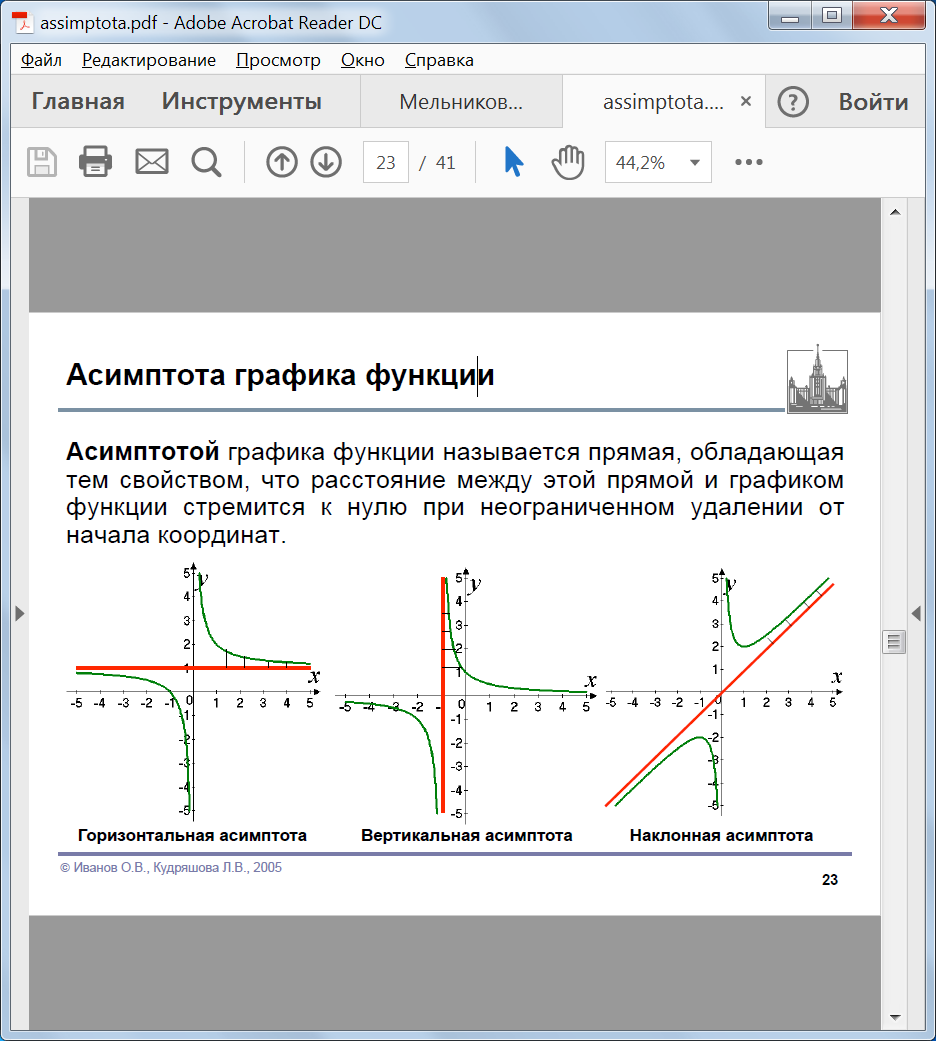
Тема 9. Графическое построение асимптот(4 часа)Асимптотой графика функции называется прямая, обладающаятем свойством, что расстояние между этой прямой и графикомфункции стремится к нулю при неограниченном удалении отначала координат. Различают следующие типы асимптот: - вертикальная - горизонтальная - наклонная
Рис. 46. Типы асимптот Если в точке разрыва функции или граничной точке области определения хотя бы один односторонний предел бесконечен, то в этой точке есть вертикальная асимптота. График функции y = f(x) при x → aимеет вертикальную асимптоту,если
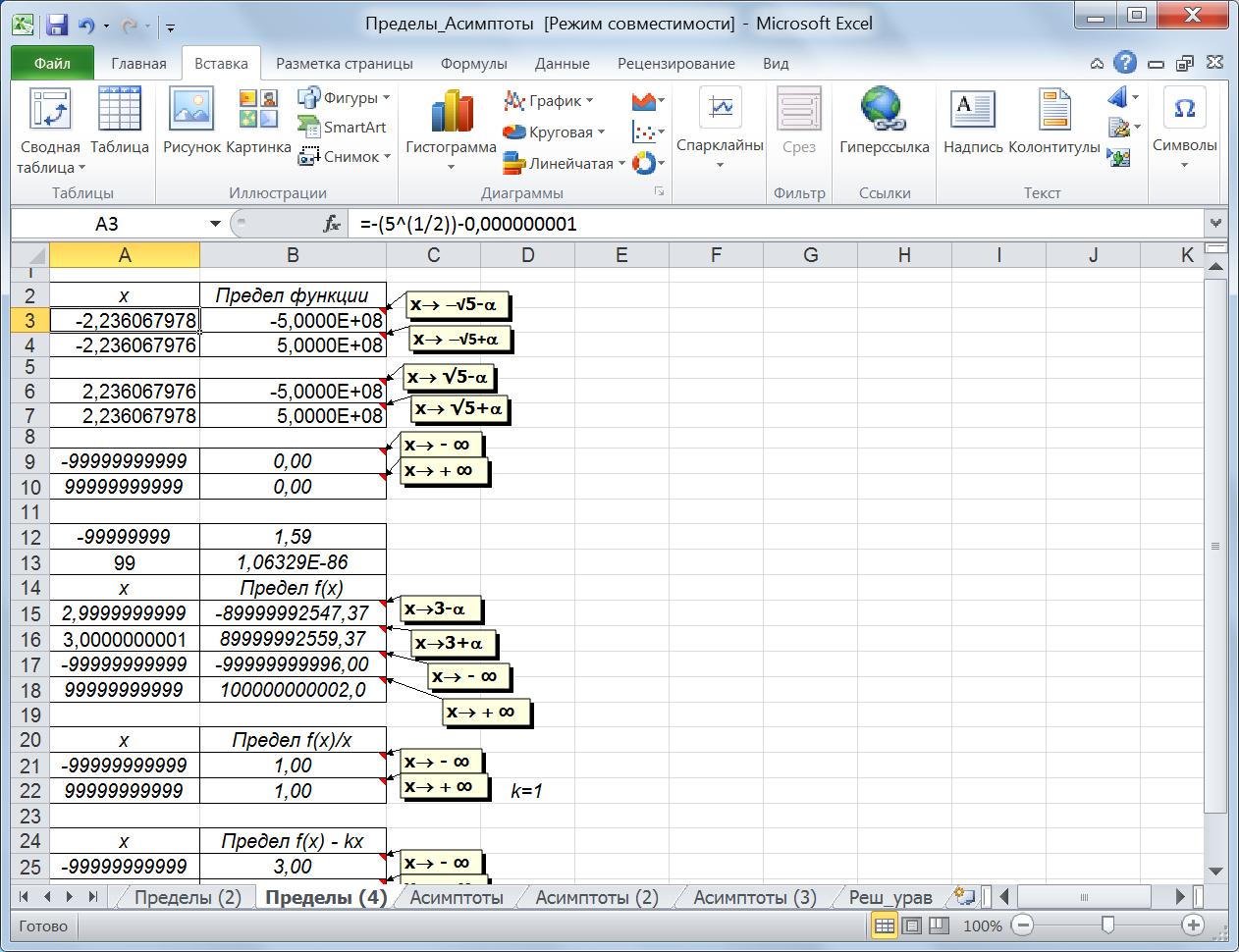
Если предел функции в ±∞ конечен, то получаем уравнение горизонтальной асимптоты, равной этому конечному значению. График функции y = f(x) при x → +∞ или x → – ∞имеет горизонтальную асимптоту,если Если в ±∞ конечного предела нет, то ищем пределы для наклонной асимптоты. Если соответствующие пределы конечны, то получаем уравнение наклонной асимптоты. Наклонной асимптотойграфика функции называется прямая y = kx+b.Для ее существования необходимо, чтобы существовали конечные пределы Пример 9.1.Проанализируемфункцию Решение. Данная функция имеет разрывы в точках Все односторонние пределы бесконечны (рис. 47), таким образом, в этих точкахесть вертикальные асимптоты:
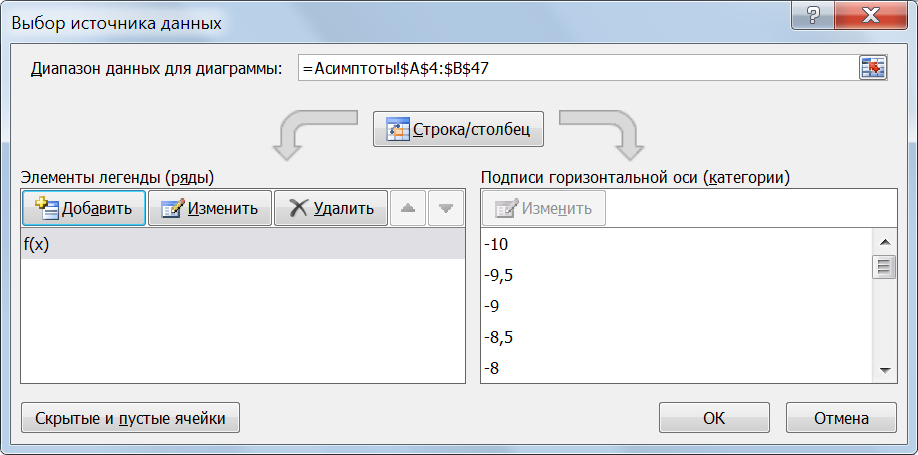
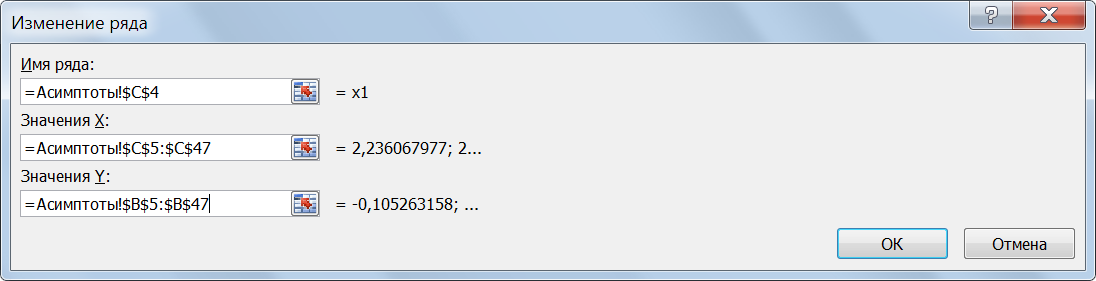
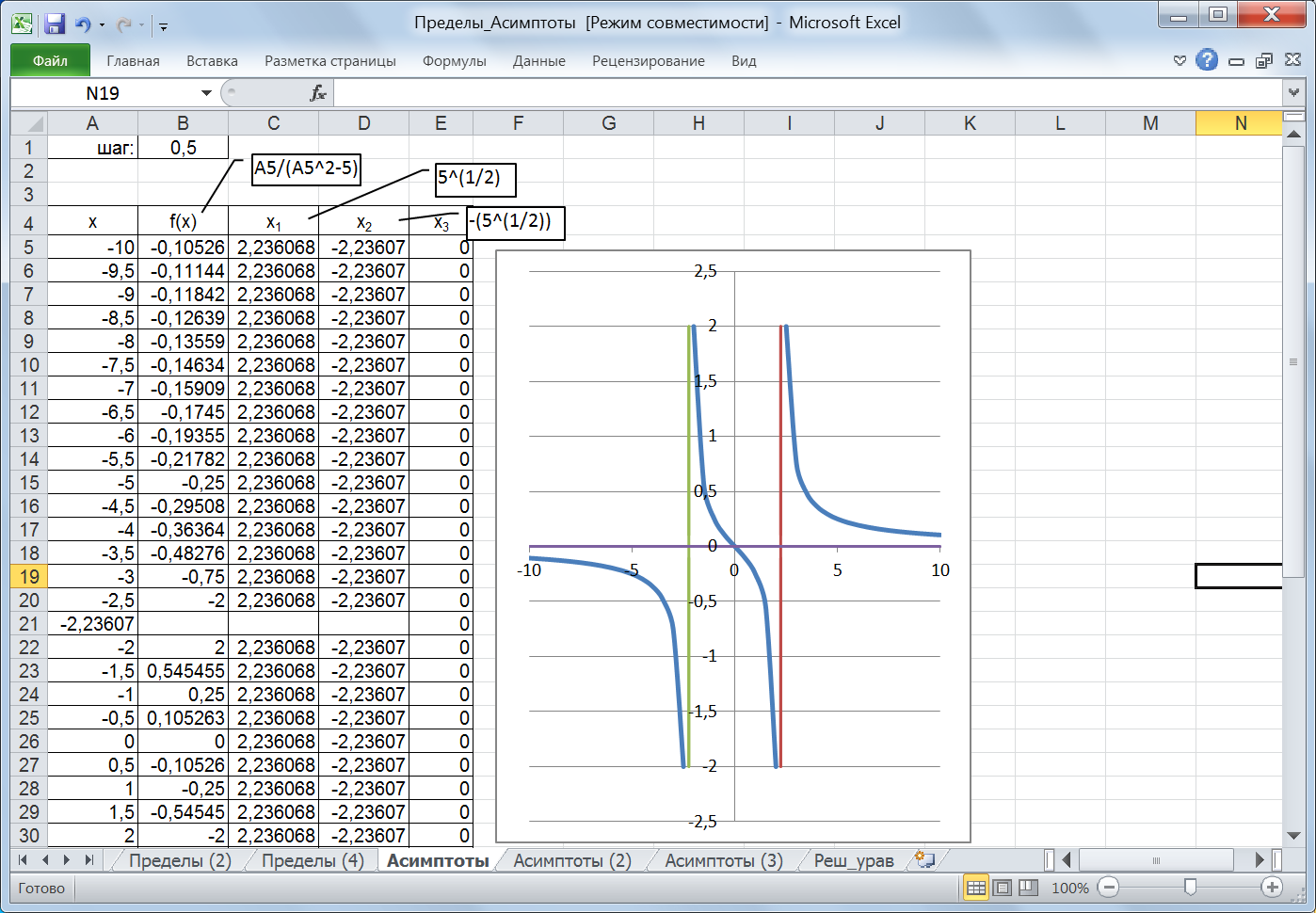
Рис. 47. Левые и правые пределы функции бесконечны Предел функции в ±∞ конечен и равен 0, получаем уравнение горизонтальной асимптоты: у1 = 0.  Построение графика функции y(x)осуществим на отрезке [-10; 10] с шагом 0,5(шаг изменения аргумента занесем в ячейку B1).Начальное значение аргумента занесем в ячейку A5, а в ячейку А6занесем формулу вычисления следующего значения аргумента:=A5+$B$1. Дополнительно вставим по одной пустой ячейке между значениями:-2,5 и-2; между 2 и 2,5. В эти ячейки введем значения В ячейки С5 и D5 занесем формулы для асимптот и скопируем ее в другие ячейки. На рисунке 48 приведен результат получения рядов данных для построения графика функции и асимптот. На основании полученных данных построим график функции, горизонтальную асимптоту и две вертикальных асимптоты. Для построения графика функции выделим диапазон А4:В47 и построим точечную диаграмму. Для построения первойвертикальной асимптотывызовем из контекстного меню области построения диаграммы пункт «Выбрать данные» (рис. 49). В окне «Выбор источника данных» воспользуемся кнопкой «Добавить». В результате откроется окно «Изменение ряда» (рис.50).
Рис.48. Табличные значения функции и асимптот
Рис.49. Диалоговое окно выбора данных
Рис.50. Диалоговое окно изменения ряда В первой строке укажем имя второго ряда (первый ряд – это функция), выбрав содержимое ячейкиС4, во второй строке укажем значения аргумента, выделив диапазон С5:С47, в третьей строке укажемзначение функции (предварительно убрав все имевшиеся в ней символы), выделив диапазон В5-В47.Завершим ввод данных нажатием на кнопку «ОК». Для построения второй вертикальной асимптоты повторим действия, указав в качестве имени рядасодержимое ячейкиD4, в качествезначения аргумента – диапазон D5:D47, вкачествезначения функции – диапазон В5-В47. Для построения горизонтальной асимптоты выполним те же действия, в качестве значения аргумента укажем диапазон А5:А47, вкачествезначения функции – диапазон Е5-Е47. Результат построения представлен на рисунке 51.
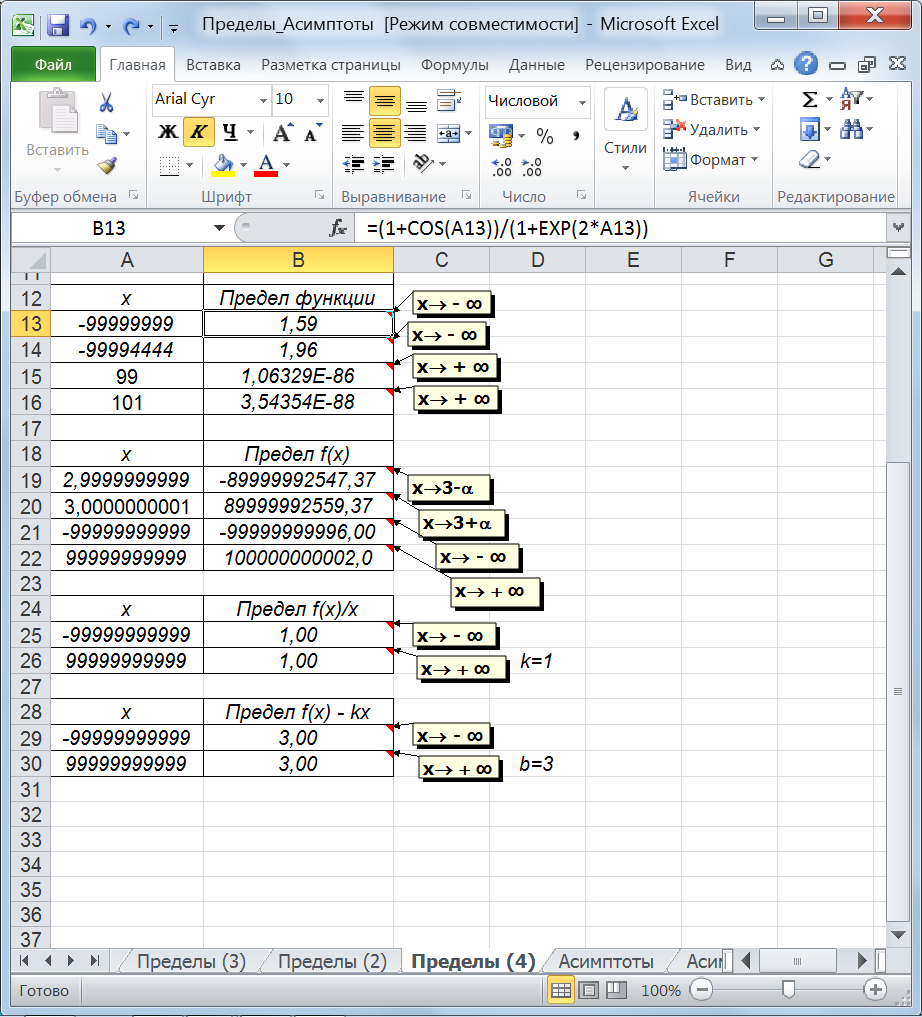
Рис.51. График функции с асимптотами Пример 9.2.Построим график функции Решение. Данная функция имеет разрыв в точке х = 3. Найдем пределы функции в этой точке и на ±∞ (рис. 52). Все эти пределы бесконечны. Таким образом, можно сделать вывод о наличии вертикальной асимптоты х = 3 и об отсутствии горизонтальных асимптот. Для ответа на вопрос о наличии наклонных асимптот найдем предел f(x)/x на ±∞, он равен 1. Предел f(x)–kxравен 3, отсюда следует, что наклонная асимптота имеет вид: y = x + 3.
Рис. 52. Пределы функции и для наклонной асимптоты Область определения: хϵ(-∞;3)U(3;+∞). Выберем из области определения подходящий диапазон и шаг для построения функции. Результат построения представлен на рисунке 53.
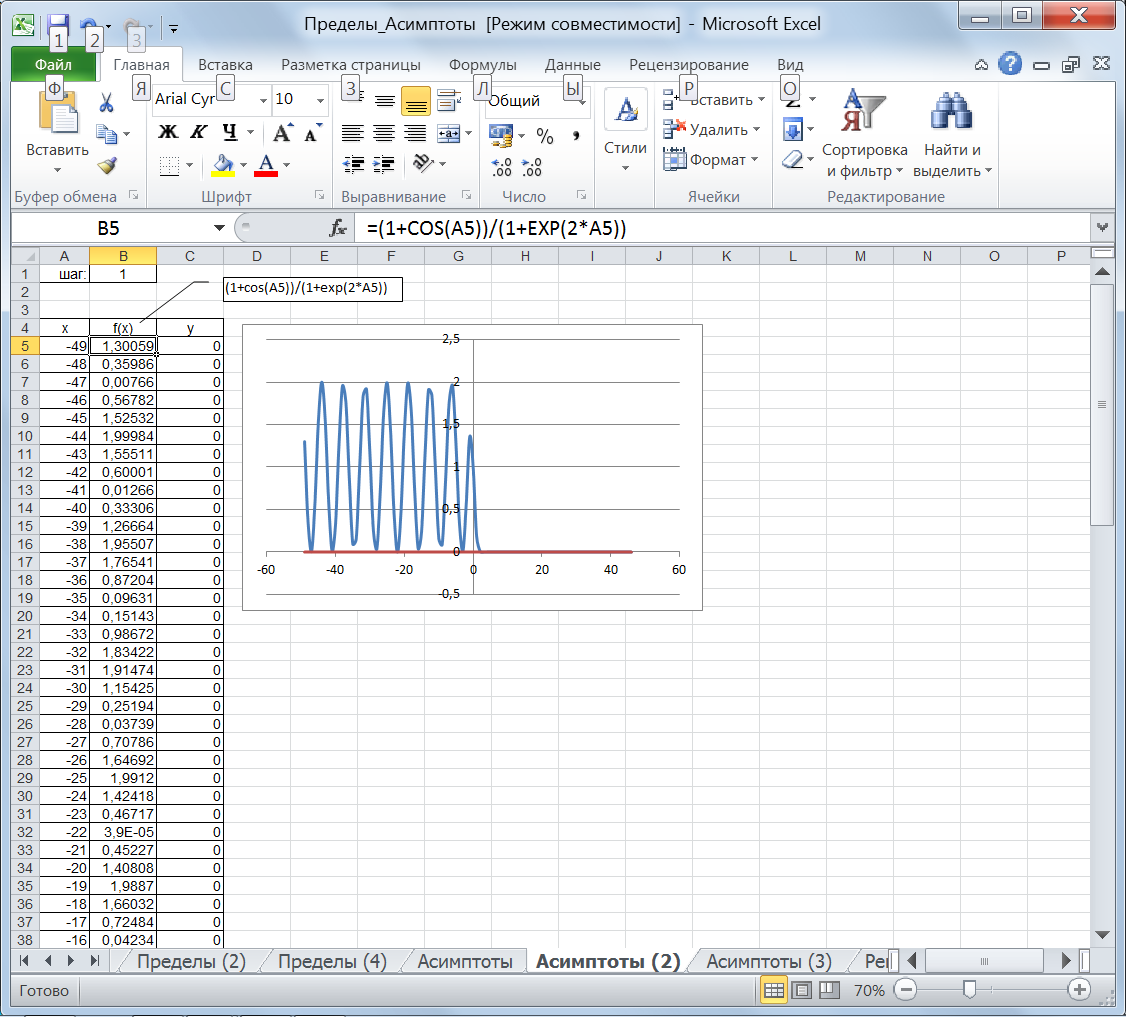
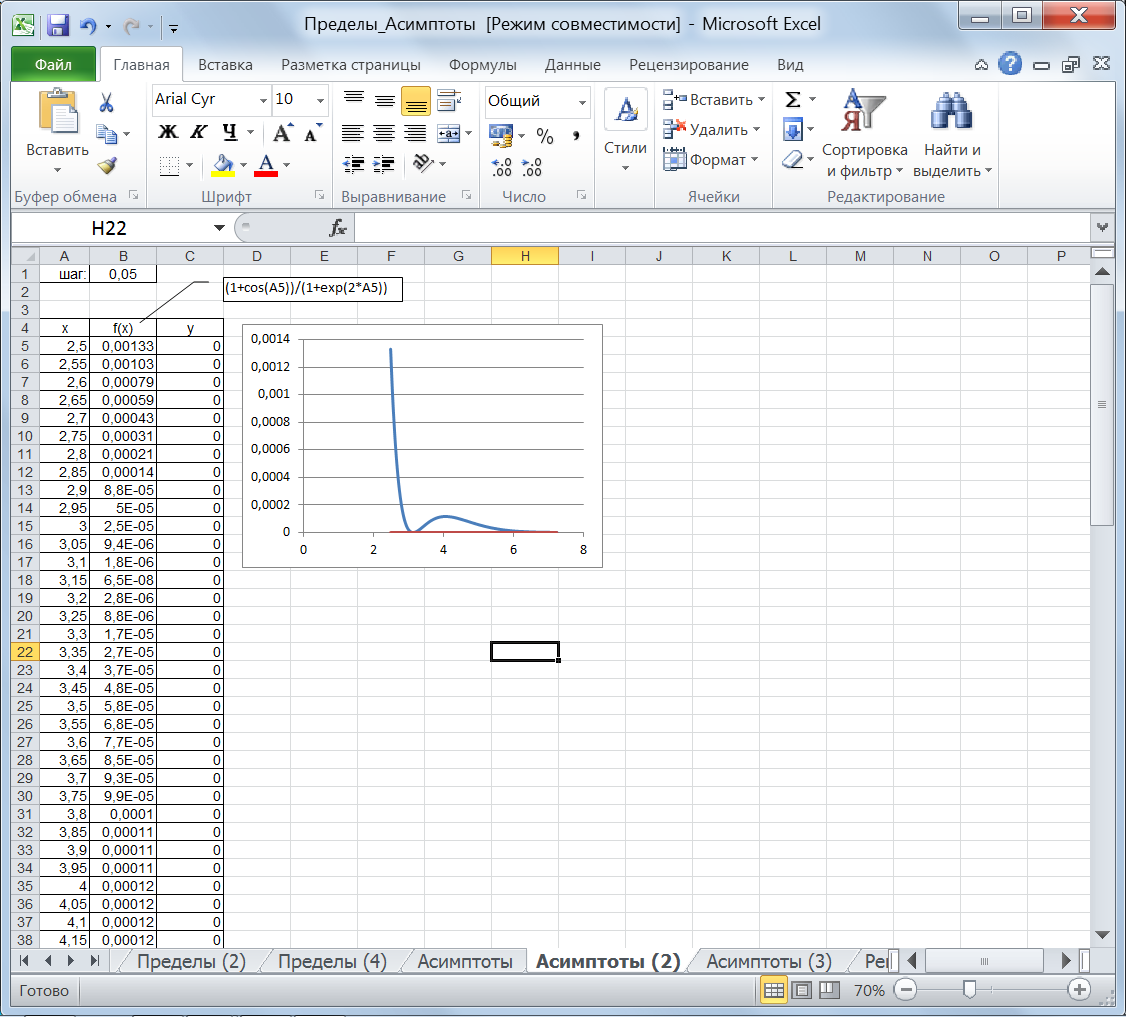
Рис. 53. График функции с асимптотами Пример 9.3.Построим график функции Решение. Данная функция не имеет точек разрываона определена на всем промежутке (-∞; +∞). Найдем пределы функции на бесконечности (рис. 54). Если полученный конечный предел на -∞ противоречит внешнему виду функции и ожидаемому отсутствию конечного предела, то необходимо найти пределы еще в некоторых точках на -∞ (рис. 54). Конечные пределы не совпадают, что свидетельствует о бесконечном пределе на -∞. Пределы на +∞ равны 0, т.е. существует горизонтальная асимптота у = 0. График функции с асимптотой представлен на рисунке 55. Для более детального анализа функции в положительной области х поменяем в таблице начальное значение на 2,5 и шаг на 0,05, на рисунке 56 видно изменение в поведении функции, и ее периодическое приближение к асимптоте.
Рис. 54. Пределы функции
Рис. 55. График функции с асимптотой
Рис. 56. График функции с асимптотой |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 564. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
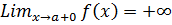 или
или 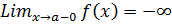 .При этом точка x = a есть точка разрыва. Уравнение вертикальной асимптоты имеет вид: x=a.
.При этом точка x = a есть точка разрыва. Уравнение вертикальной асимптоты имеет вид: x=a.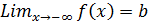 и (или)
и (или) 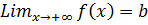 .Уравнение горизонтальной асимптоты имеет вид: y=b.
.Уравнение горизонтальной асимптоты имеет вид: y=b.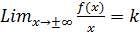 и
и 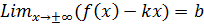 .
.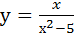 и построим графикфункции и асимптоты.
и построим графикфункции и асимптоты.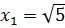 (2,23607) и
(2,23607) и 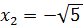 (-2,23607). Найдем пределы функции в окрестностях точек разрыва и пределы функции на ±∞.
(-2,23607). Найдем пределы функции в окрестностях точек разрыва и пределы функции на ±∞.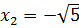 .
.
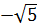 (–2,23607) и
(–2,23607) и 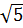 (2,23607) соответственно. В ячейкуВ5 введем функцию (=A5/((A5^2)-5)), формулу скопируем на весь столбец, и из ячеек В21 и В31 удалим бесконечно большие значения (-2,5Е+15), так как в этих точках функция разрывная.
(2,23607) соответственно. В ячейкуВ5 введем функцию (=A5/((A5^2)-5)), формулу скопируем на весь столбец, и из ячеек В21 и В31 удалим бесконечно большие значения (-2,5Е+15), так как в этих точках функция разрывная.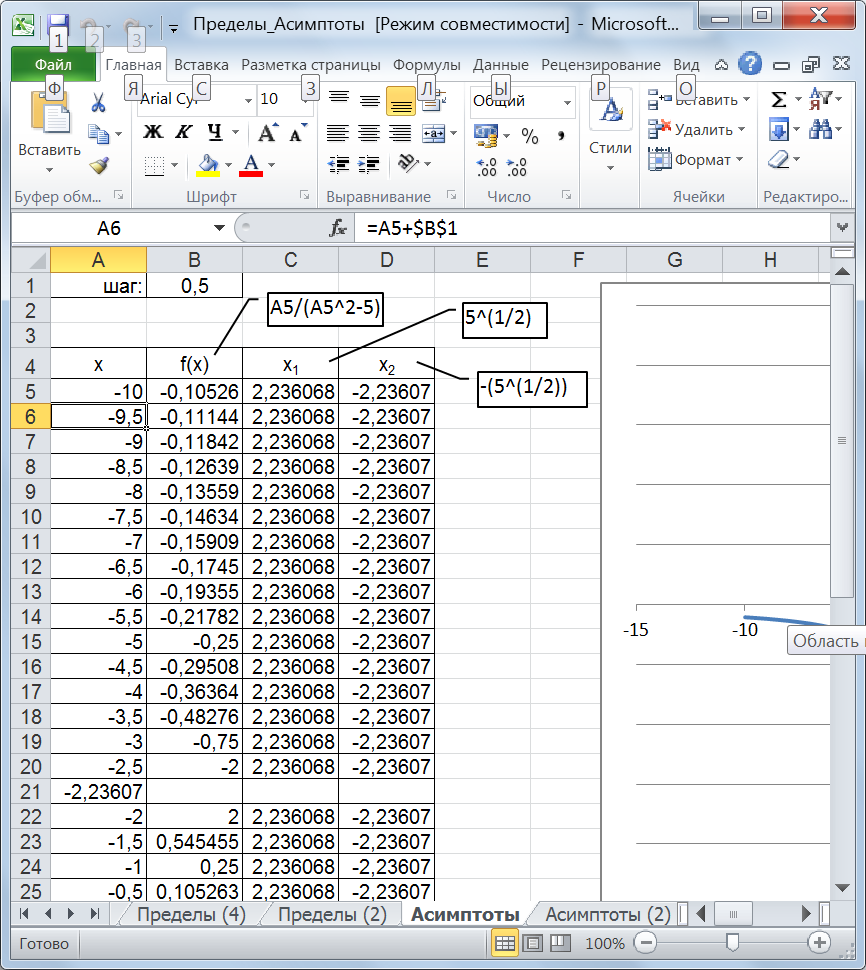
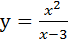 и ее асимптоты.
и ее асимптоты.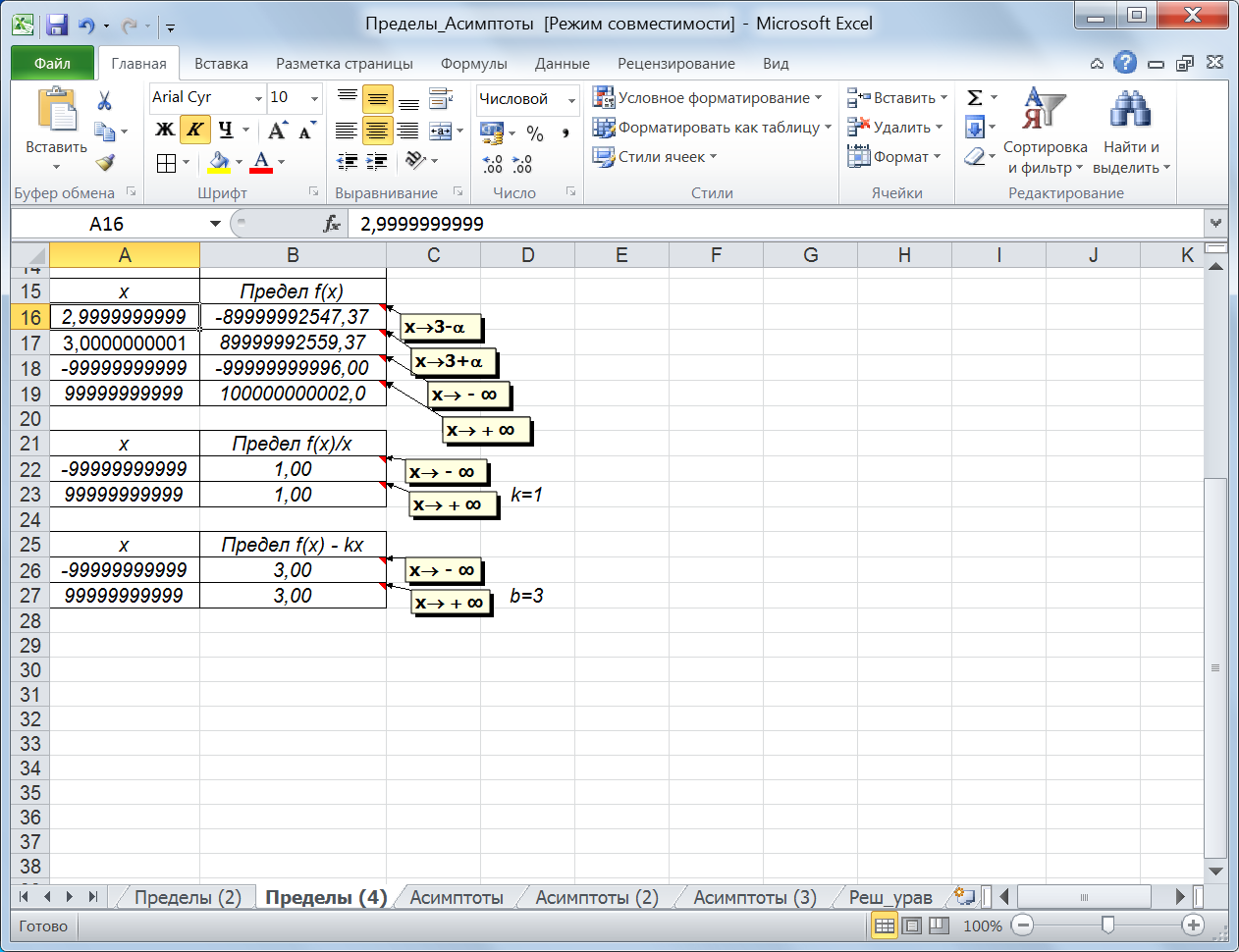
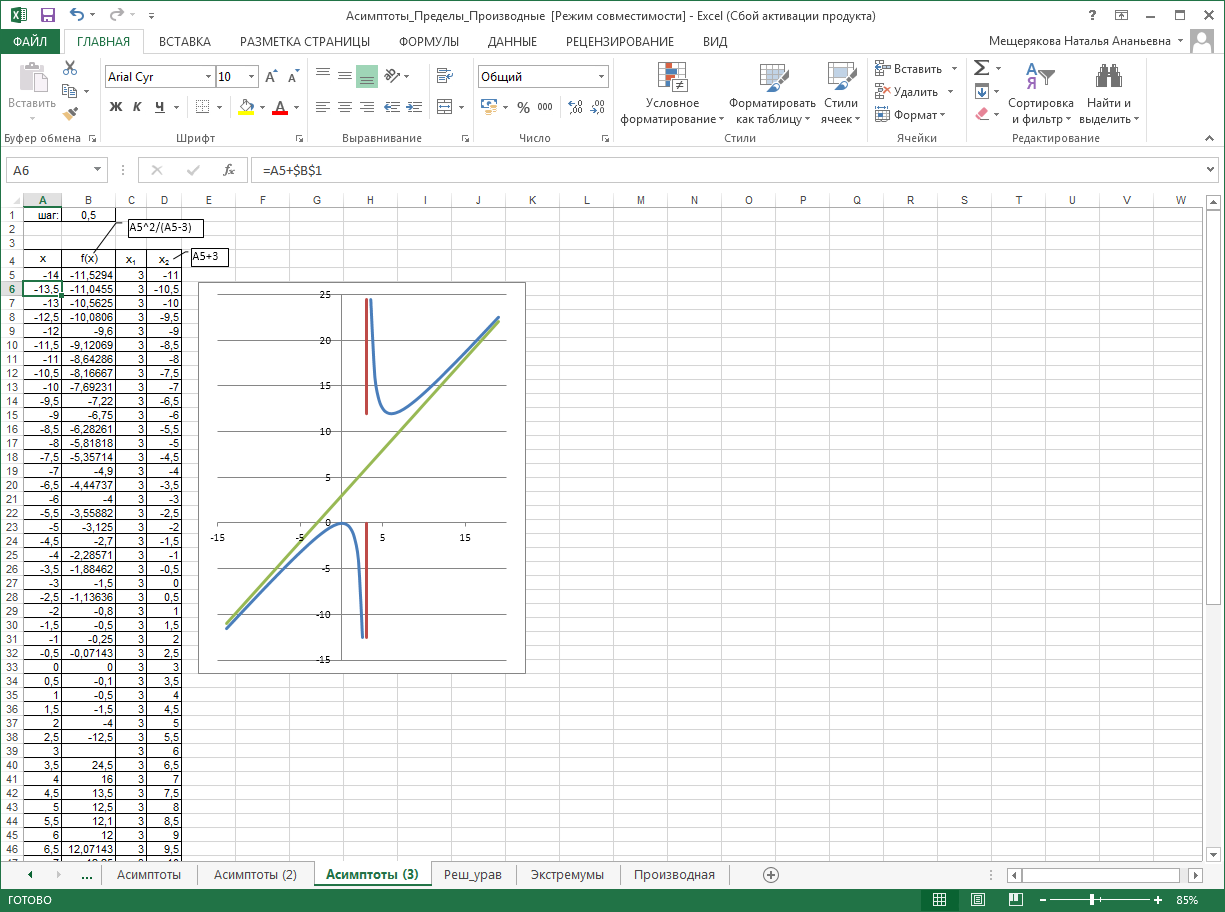
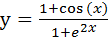 и ее асимптоты.
и ее асимптоты.