
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление предела числовой последовательностиЧисло a ∈ Rназываетсяпределомчисловойпоследовательности {xn}, еслипоследовательность{xn – а} является бесконечно малой, то есть все её элементы, начиная с некоторого, по модулю меньше любого заранее определенного положительного числа.
Если число a ∈ Rявляетсяпределомчисловойпоследовательности{xn}, тоговоряттакже, чтопоследовательность{xn}сходится к a. Если никакое вещественное число не является пределом последовательности {xn}, её называют расходящейся. Для некоторых последовательностей предел полагают равным бесконечности. А именно, говорят, что последовательность {xn} стремится к бесконечности, если для любого вещественного числа все члены последовательности, начиная с некоторого, оказываются по модулю больше этого числа. Формально,
Рассмотрим технологию приближенного вычисления предела числовой последовательности. В некоторую ячейку листа Excel вводится большое число, например, 1012. В соседнюю ячейку вводится функция, которая в качестве аргумента будет иметь ячейку с введенным большим числом. Полученное в этой ячейке значение и будет искомым пределом функции. Вычисление предела функции Функция f(x) имеет предел в точке а тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. Используя электронную таблицуExcelдля нахождения предела функции можно применить следующую технологию: в две ячейки на рабочем листе ввести числа, близкие к точке а слева и справа, всоседние к ним ячейки рабочего листа ввести одинаковые формулы, соответствующиевыражениюфункциональной зависимости, в которых значения аргумента указываются адресными ссылками на ячейки с числами, близкими к а. Если в ячейках получим одно и то же значение, то оно и будет искомым пределом.  При нахождении предела функции при х ® ∞ в ячейку с аргументом введите достаточно большое число. Пример 8.1. Найдите предел числовой последовательности {n/(n+1)}. Решение. В ячейку А2 введем большое число, примерно равное 1012. В ячейку рабочего листа В2 введем формулу =A2/(A2+1). После ввода числа в ячейке В2 отобразится приближенное значение предела числовой последовательности (рис. 41).
Рис. 41. Нахождение предела последовательности Пример 8.2. Пусть начальный вклад равен 1000 денежных единиц, процентная ставка составляет 10% годовых, начисление процентов непрерывное. Требуетсяопределить, какая сумма вклада будет по истечении двух лет. Решение. Известно, что формула сложных процентов имеет вид:
Необходимо найти Введем исходные данные на рабочий листExcel, как представлено на рисунке42 идостаточно большое число m. В ячейку Е2 введем формулу для вычисления суммы вклада по истечении двух лет(наращенной суммы): =D2*(1+B2/A2)^(A2*C2). Результат вычисления приведен на рисунке40:S(t) = 1221,2075 рублей.
Рис. 42. Нахождение наращенной суммы при непрерывном начислении процентов
Пример 8.3. Найти Решение. Введем в ячейкиА3 и А4 (рис. 43) значения, достаточно близкие кзначению 2: слева 1,99999999999 и справа – 2,00000000001. В ячейкуВ3введем формулу, реализующую аналитическое выражение= (A3^2-5*A3+6)/(A3^2-3*A3+2), которую скопируем в ячейку В4.После вычисления можно заметить, что значения в ячейках В3 иВ4 совпадают, значит это и есть приближенное значение предела функции.
Рис. 43. Нахождение предела функции Пример 8.4. Найти Решение. Введем в ячейкуА3достаточно большое число (рис. 44). В ячейкуВ3введем формулу, реализующую аналитическое выражение= (4*A3+2)/(A3+1).Значение, полученное в ячейкеВ3, и есть приближенное значение предела функции.
Рис. 44. Нахождение предела функции Пример 8.5.Исследовать поведение функции спросау = 100/(х + 5)принеограниченном увеличении цены х (x®∞). Решение. Введем в ячейкуА3достаточно большое число (рис. 45). В ячейкуВ3введем формулу, отображающую поведение функции спроса: = 100/(A3+5).
Рис. 45. Нахождение предела функции Мы получили очень ожидаемый результат – при увеличении цены до бесконечности спрос стремится к нулю!
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 541. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



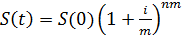 ,где i – номинальная годовая ставка сложных процентов; m – число начислений в году, n – количество лет.
,где i – номинальная годовая ставка сложных процентов; m – число начислений в году, n – количество лет.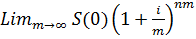 .
.
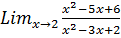 .
.
 .
.
