
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Типовые звенья и передат ф-ии(уже есть).интегрирующеее звено.Ду,передат и переходн хар-киДифференциальное уравнение интегрирующего звена имеет вид:
Коэффициент
Записываем дифференциальное уравнение звена (2.10) в алгебраической операторной форме, получим:
откуда находим передаточную функцию звена:
Дифференциальное уравнение интегрирующего звена можно записать в другой форме:
При этом передаточная функция звена примет вид: На рис. 2.4 представлен характер изменения выходной величины интегрирующего звена при подаче на его вход постоянной входной величины
Рис. 2.4 Передаточная функция и переходный процесс интегрирующего звена
Тогда из уравнения (2.11) получим
если входное воздействие является единичным, т.е.
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 2.5.
Рис. 2.5. Примеры реализации интегрирующих звеньев
Часто в качестве такого звена используется операционный усилитель в режиме интегрирования. Интегрирующим звеном является также обычный гидравлический демпфер (рис.2.5, б). Входной величиной здесь является сила 
где Часто в качестве интегрирующего звена используется интегрирующий привод (рис. 2.5, г). Это особенно удобно делать при необходимости длительного интегрирования. Примечание: Здесь и в дальнейшем будем иметь ввиду следующие соответствия ( |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 426. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (2.10)
(2.10) называется коэффициентом усиления интегрирующего звена. При нулевых начальных условиях (т.е если при
называется коэффициентом усиления интегрирующего звена. При нулевых начальных условиях (т.е если при  имеем
имеем  ) у интегрирующего звена выходная величина пропорциональна интегралу входной величины:
) у интегрирующего звена выходная величина пропорциональна интегралу входной величины:
 ,
, (2.11)
(2.11)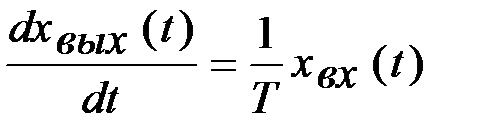 , где
, где  .
. (2.12)
(2.12)
 А(амплитуда), изображение которой (см. приложение 1)
А(амплитуда), изображение которой (см. приложение 1)  .
.
 как реакцию звена (цепи) на единичное входное воздействие, выраженную в алгебраической форме. Запишем данное равенство в форме оригинала функции, выполнив обратное преобразование Лапласа:
как реакцию звена (цепи) на единичное входное воздействие, выраженную в алгебраической форме. Запишем данное равенство в форме оригинала функции, выполнив обратное преобразование Лапласа: , (2.13)
, (2.13) соответствует
соответствует  , или по таблице Лапласа -
, или по таблице Лапласа -  , тогда преобразование можно записать:
, тогда преобразование можно записать: (2.14)
(2.14)
 , действующая на поршень, а выходной перемещение поршня
, действующая на поршень, а выходной перемещение поршня  . Так как скорость движения поршня пропорционально приложенной силе (без учета инерционных сил):
. Так как скорость движения поршня пропорционально приложенной силе (без учета инерционных сил): ,
, – коэффициент скоростного сопротивления, его перемещение будет пропорциональным интегралу от приложенной силы:
– коэффициент скоростного сопротивления, его перемещение будет пропорциональным интегралу от приложенной силы: 
 ).
).