
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Типовые звенья и их передат ф-ии. Запаздывающее звено. ДУ,передат и переход хар-ки.Выходная величина в запаздывающем звене точно повторяет входную величину, но с некоторым запаздыванием на величину
Для определения передаточной функции звена найдем изображение выходной величины по Лапласу:
Вынося постоянную величину
Так как согласно формуле (2.7)
Таким образом, запаздывающее звено имеет передаточную функцию
Переходный процесс запаздывающего звена при ступенчатом изменении входной величины на
Рис. 2.17. Передаточная функция и переходный
Соединение звеньев,передат ф-ии соединений,последоват соед-е звеньев. В системах автоматического регулирования звенья могут соединяться в самых различных сочетаниях. Однако систему любой сложности можно всегда рассматривать как совокупность трех видов соединений элементарных звеньев: последовательного, параллельного и встречно-параллельного. Последовательное соединение звеньев При последовательном соединении звеньев выходная величина предыдущего звена является входной величиной последующего.
Рис. 3.32. Последовательное соединение звеньев Так, для трех последовательно соединенных звеньев, изображенных на рис. 3.32, можно записать: Входной величиной  В соответствии с выражением
Учитывая, что
Так как передаточная функция соединения в целом равна Таким образом, передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. В качестве примера определим передаточную функцию системы, состоящей из двух последовательно соединенных инерционных звеньев первого порядка: Передаточная функция всей системы
Из этого примера следует важный для практики вывод, что два последовательно соединенных инерционных звена первого порядка создают одно инерционное звено второго порядка. При этом оно не может быть колебательным, если корни его характеристического уравнения вещественны и отрицательны: Коэффициент передачи системы В свою очередь любое апериодическое (неколебательное) инерционное звено второго порядка можно разбить на два элементарных инерционных звена первого порядка.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 477. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 :
: .
. . Введём новую переменную
. Введём новую переменную  , тогда запишем:
, тогда запишем: .
. за знак интеграла и учитывая, что дифференциал
за знак интеграла и учитывая, что дифференциал 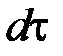 постоянной величины равен нулю, получим:
постоянной величины равен нулю, получим: .
. интеграл в этом выражении является изображением
интеграл в этом выражении является изображением  функции
функции  , получим:
, получим: .
. . (2.53)
. (2.53) представлен на рис. 2.16.
представлен на рис. 2.16.

 .
. всего соединения служит входная величина первого звена. Выходной величиной
всего соединения служит входная величина первого звена. Выходной величиной  соединения является выходная величина последнего звена.
соединения является выходная величина последнего звена.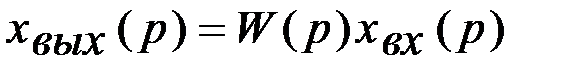 имеем:
имеем:
 и
и  , находим:
, находим: .
. , то с учетом того, что
, то с учетом того, что  и
и  , получим:
, получим:  . (3.42)
. (3.42)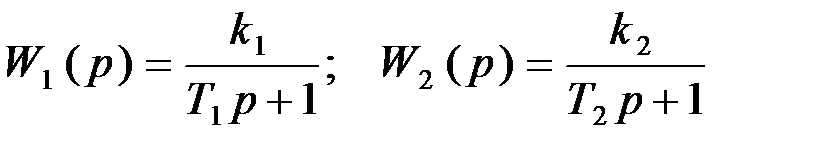 .
. .
. .
.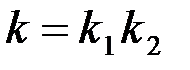 .
.