
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Соед-е звеньев,предат ф-ии соед-й. Параллель соед-е звеньев.В системах автоматического регулирования звенья могут соединяться в самых различных сочетаниях. Однако систему любой сложности можно всегда рассматривать как совокупность трех видов соединений элементарных звеньев: последовательного, параллельного и встречно-параллельного. Входная величина системы, состоящей из параллельно соединенных звеньев, одновременно подается на входы всех звеньев, а ее выходная величина равна сумме выходных величин отдельных звеньев. На рис.2.19 представлена система, состоящая из трех параллельно соединенных звеньев:
Рис.3.33. Параллельное соединение Изображения выходных величина звеньев через их передаточные функции запишутся так:
Так как то находим
Передаточная функция системы
Таким образом, передаточная функция системы, состоящая из параллельно соединенных звеньев, равна сумме передаточных функций этих звеньев. Например, при параллельном соединении инерционного звена первого порядка с усилительным (безынерционным) звеном получим:
откуда
Это интегро-дифференцирующее звено (см. выражение 2.29), постоянные времени и коэффициент передачи которого равны:
Из приведенного примера следует, что любое интегро-дифференцирующее звено можно представить в виде инерционного звена первого порядка и усилительного (безынерционного) звена, соединенных параллельно.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 516. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
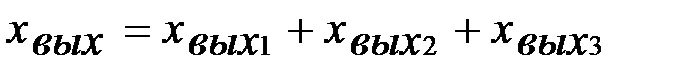 .
.

 ,
, .
. . (3.43)
. (3.43) .
. .
. .
.