
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Типовые звенья и их передат ф-ия.Интегро-дифференцир звено. ДУ,передат и переход хар-ки. Пример реализации.Интегро-дифференцирующее звено имеет дифференциальное уравнение Выполнив алгебраические преобразования, получаем передаточную функцию звена: Постоянная времени Постоянная времени Определим характер переходного процесса интегро-дифференцирующего звена при скачкообразном изменении входной величины на Изображение выходной величины По таблице Лапласа (приложение 1) найдем оригинал функции по его изображению: Переходный процесс интегро-дифференцирующего звена представлен на рис. 2.12.
интегро-дифференцирующего звена
Как следует из рисунка и выражений для переходного процесса (2.30) и передаточной функции (2.29), интегро-дифференцирующее звено при определенных относительных величинах постоянных При Так, если
Если Если 
Таким образом, интегро-дифференцирующее звено имеет большие возможности для настройки в целях получения необходимых динамических свойств систем регулирования. На рис. 2.13 даны примеры интегро-дифференцирующих звеньев. Для электрической цепи (рис. 2.13, а) можно записать:
Решив это уравнения, найдем
Передаточная функция звена соответствует выражению (2.34), при этом
Для электрической цепи (рис. 2.13, б) согласно второму закону Кирхгофа запишем:
Определив из этих уравнений значения токов через напряжения и учитывая, что по первому закону Кирхгофа найдем дифференциальное уравнение цепи (рис. 2.13, б).
Передаточная функция определяется выражением (2.29), согласно которому запишем коэффициент передачи звена и постоянные времени
При
8.Типовые звенья и их предат ф-ии. Инерц звено 2-го порядка.ДУ,передаточ хар-ка и переходн процессы при различ хначениях отношений Т1/Т2>2 , =2 и <2. Инерционное звено второго порядка имеет дифференциальное уравнение Передаточная функция звена либо, разложив соотношение на линейные множители Переходный процесс инерционного звена второго порядка можно исследовать путем аналитического решения дифференциального уравнения (2.31), которое является неоднородным линейным дифференциальным уравнением второго порядка. Для получения общего решения неоднородного дифференциального уравнения достаточно к какому-либо частному решению его прибавить общее решение однородного с ним уравнения, т.е. уравнения, в котором Одним из частных решений неоднородного уравнения (2.34) при скачкообразном (ступенчатом) изменении Так как производная постоянной величины равна нулю, то частное решение неоднородного уравнения (2.34) при новом состоянии равновесия системы после входного воздействия будет иметь вид: Однородное дифференциальное уравнение получим из уравнения (2.34) при
Его характеристическое уравнение имеет вид:
что получается, если приравнять нулю оператор левой части неоднородного дифференциального уравнения, или, что есть то же самое, приравнять нулю знаменатель передаточной функции Характеристическое уравнение в общем случае может иметь Определив все корни характеристического уравнения, общее решение однородного дифференциального уравнения можно найти по известной формуле
где Для дифференциального уравнения (2.31), характеристическое уравнение (2.37) примет вид:
Корни характеристического уравнения (2.39)
Частное решение дифференциального уравнения (2.31) инерционного звена второго порядка как вынужденная составляющая переходного процесса согласно (2.35) будет:
Характер переходного процесса звена или цепи, определяемого дифференциальным уравнением (2.31), зависит от расположения на комплексной плоскости корней его характеристического уравнения, следовательно – от знака подкоренного выражения (2.40). Здесь могут возникнуть три случая. 1. При Тогда согласно уравнению (2.38) общее решение однородного уравнения инерционного звена второго порядка как свободная составляющая переходного процесса, имеет вид:
Прибавив к нему частное решение неоднородного дифференциального уравнения (2.41) получим общее решение неоднородного дифференциального уравнения (2.31) переходного процесса инерционного звена второго порядка при
Так как до подачи входного воздействия система находилась в равновесии, то при Следовательно, исходя из начальных условий, находим:
Решив эти уравнения, получим: Таким образом, переходный процесс звена при
Производя обратное преобразование Лапласа, найдем для апериодического режима передаточной функции (2.33) инерционного звена второго порядка соответствие между оригиналом и изображением, имея в виду, что
Таким образом, получили табличную форму преобразования Лапласа (см. Приложение 1). 2. При
Согласно (2.38) находим свободную составляющую переходного процесса
Общее решение уравнения (2.31) как сумма свободной и вынужденной составляющих переходного процесса для этого случая
Производная выходной величины Так как при
находим:
Таким образом, окончательно переходный процесс звена при
Обратный переход по Лапласу для случая двух одинаковых корней выглядит следующим образом:
Переходный процесс звена (элемента системы) является граничным при переходе от апериодического режима переходного процесса к колебательному. 3. При
где
Запишем уравнение переходной характеристики в алгебраической форме для случая периодического переходного процесса
Обозначим По таблице Лапласа (приложение 1) найдем оригиналы:
В соответствии с теоремой свертки находим оригинал функции
иначе
Таким образом, переходный процесс звена при Переходные процессы колебательного звена в зависимости от отношения
инерционного звена второго порядка (колебательного) при различных значениях отношения Как известно, мнимая составляющая
Как следует из рис.2.15, а, Так как
Рис. 2.15 Переходные процессы
Чем ближе к единице величина Степень затухания зависит от отношения вещественной составляющей комплексных корней характеристического уравнения где
4. При Подставив эти значения в выражение (2.49) для переходного процесса колебательного звена, получим
Такое колебательное звено называется консервативным. Переходный процесс в этом случае незатухающим колебательным, т.к. Чем больше
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 529. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. характеризует степень влияния производной
характеризует степень влияния производной  на закон регулирования.
на закон регулирования. отражает зависимость закона регулирования от интегральной составляющей.
отражает зависимость закона регулирования от интегральной составляющей. .
.
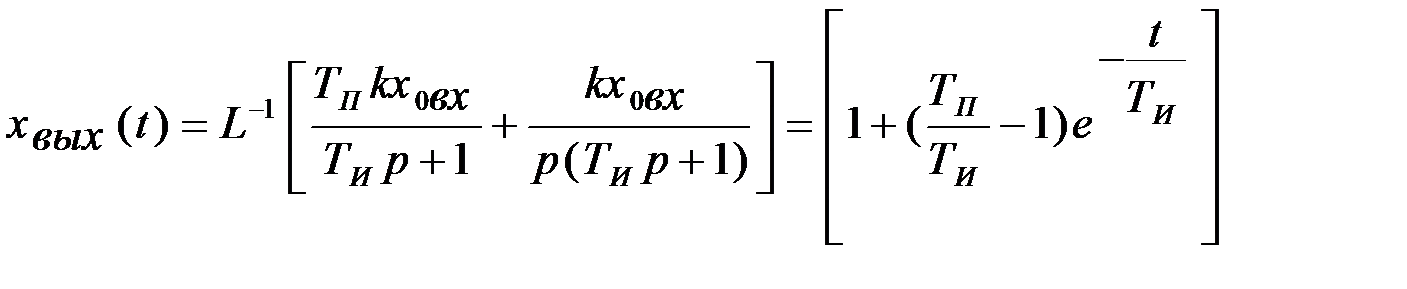

 ,
,  и
и  может приобрести динамические свойства, приближающие его к интегрирующему, дифференцирующему или инерционному звену первого порядка.
может приобрести динамические свойства, приближающие его к интегрирующему, дифференцирующему или инерционному звену первого порядка. интегро-дифференцирующее звено по своим динамическим свойствам больше приближается к дифференцирующему звену, а при
интегро-дифференцирующее звено по своим динамическим свойствам больше приближается к дифференцирующему звену, а при  – к интегрирующему звену.
– к интегрирующему звену. близко к нулю, а
близко к нулю, а  , но при этом отношение
, но при этом отношение  – конечная постоянная величина, получаем интегрирующее звено с коэффициентом передачи
– конечная постоянная величина, получаем интегрирующее звено с коэффициентом передачи  .
. и
и  стремятся к нулю, а
стремятся к нулю, а  , но произведение
, но произведение  конечная и постоянная величина, получаем идеальное дифференцирующее звено с коэффициентом передачи
конечная и постоянная величина, получаем идеальное дифференцирующее звено с коэффициентом передачи  .
. , а
, а  являются конечными величинами, получаем инерционной звено первого порядка с передаточной функцией
являются конечными величинами, получаем инерционной звено первого порядка с передаточной функцией .
.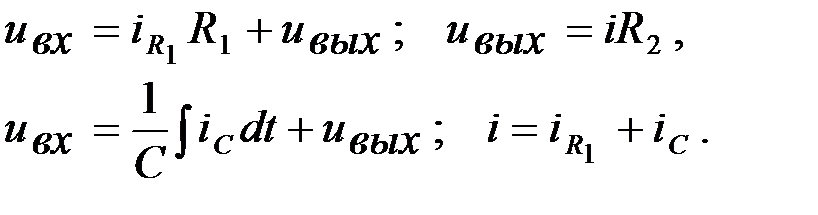

 .
.

 ,
, .
. .
. схема на (рис. 2.13, в) в соответствии с передаточной функцией приобретает следующие параметры
схема на (рис. 2.13, в) в соответствии с передаточной функцией приобретает следующие параметры .
.
 ,
, 

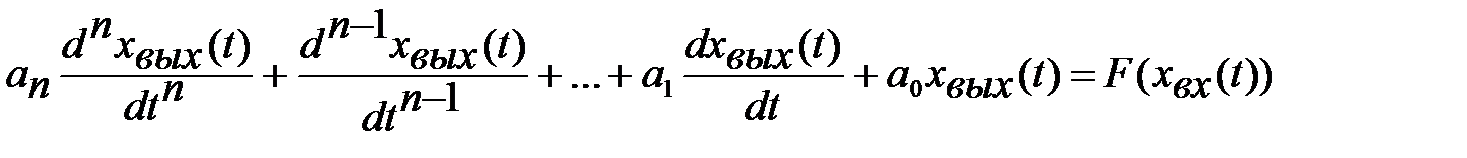
 .
. будет новое значение выхода
будет новое значение выхода  , установившееся после окончания переходного процесса.
, установившееся после окончания переходного процесса.
 :
: (2.36)
(2.36)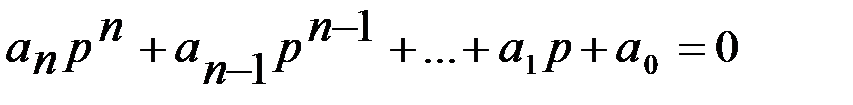 , (2.37)
, (2.37) звена.
звена. одинаковых корней
одинаковых корней  и, помимо того,
и, помимо того,  неодинаковых корней
неодинаковых корней  .
. (2.38)
(2.38) – постоянные интегрирования, которые находятся из начальных условий.
– постоянные интегрирования, которые находятся из начальных условий. (2.39)
(2.39) . (2.40)
. (2.40) , обозначим его
, обозначим его  . (2.41)
. (2.41) оба корня характеристического уравнения вещественные отрицательные:
оба корня характеристического уравнения вещественные отрицательные:  .
. , обозначим его
, обозначим его  .
. :
: .
. имеем:
имеем:  .
.
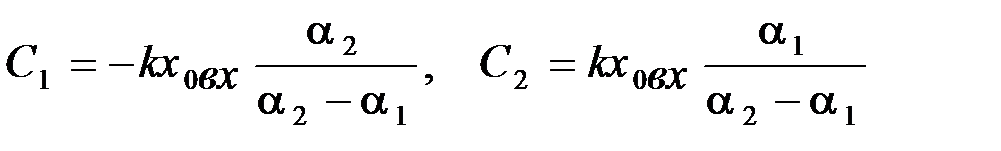
 определяется аналитическим выражением оригинала функции
определяется аналитическим выражением оригинала функции (2.42)
(2.42) и
и  .
.
 характеристическое уравнение имеет два равных вещественных отрицательных корня (дискриминант равен нулю):
характеристическое уравнение имеет два равных вещественных отрицательных корня (дискриминант равен нулю): .
. .
. .
.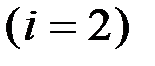 .
.

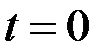 имеем:
имеем: 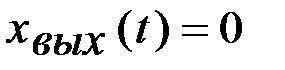 и
и  , то из уравнений (2.44) и (2.45)
, то из уравнений (2.44) и (2.45)

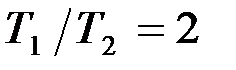 описывается выражением для оригинала
описывается выражением для оригинала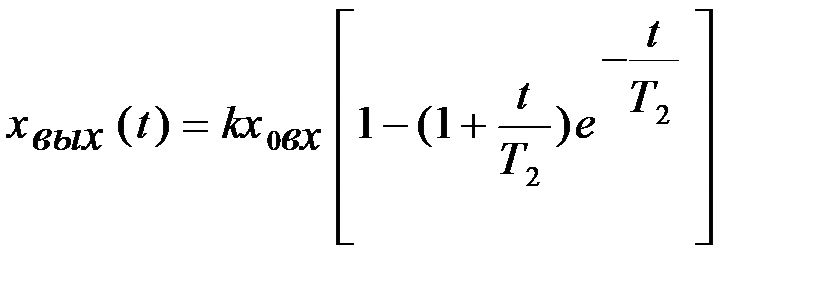 . (2.46)
. (2.46) (2.47)
(2.47) алгебраическая форма характеристического уравнения имеет два сопряженных комплексных корня:
алгебраическая форма характеристического уравнения имеет два сопряженных комплексных корня:
 .
. (2.48)
(2.48) ,
,  ,
, ,
,  .
.
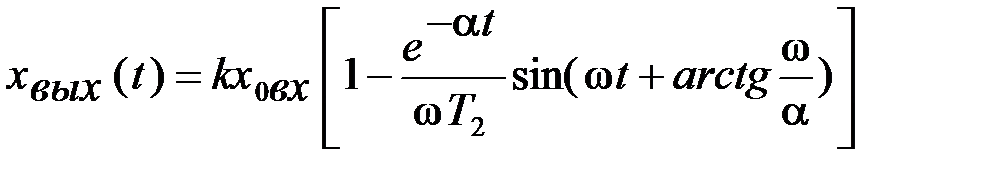 . (2.49)
. (2.49) , характеризуемый уравнением (2.49), периодичен и представляет собой затухающую синусоиду, амплитуда которой убывает от полупериода к полупериоду по экспоненциальному закону
, характеризуемый уравнением (2.49), периодичен и представляет собой затухающую синусоиду, амплитуда которой убывает от полупериода к полупериоду по экспоненциальному закону  . Такое звено нельзя представить в виде последовательного соединения других звеньев, оно относится к типовым звеньям и называется колебательным.
. Такое звено нельзя представить в виде последовательного соединения других звеньев, оно относится к типовым звеньям и называется колебательным.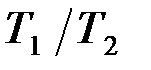 приведены на рис. (2.14).
приведены на рис. (2.14).
 .
. корней характеристического уравнения является угловой частотой колебательного звена. Период колебаний
корней характеристического уравнения является угловой частотой колебательного звена. Период колебаний  . Оценкой переходного процесса колебательного звена служит степень затухания колебаний. Степенью затухания
. Оценкой переходного процесса колебательного звена служит степень затухания колебаний. Степенью затухания  называют отношение разности двух соседних амплитуд одного знака к первой из них (рис. 2.15, а):
называют отношение разности двух соседних амплитуд одного знака к первой из них (рис. 2.15, а): . (2.50)
. (2.50) ,
,  .
. , то подставив А1 и А2 в (3.50), получим:
, то подставив А1 и А2 в (3.50), получим: . (2.51)
. (2.51)
 и
и 
 , тем быстрее затухают колебания переходного процесса.
, тем быстрее затухают колебания переходного процесса. к их мнимой составляющей
к их мнимой составляющей  . В свою очередь это отношение определяется отношением постоянных времени
. В свою очередь это отношение определяется отношением постоянных времени  :
:  ,
, – параметр затухания.
– параметр затухания. ,
, 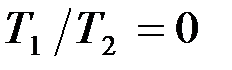 вещественная и мнимая составляющие корней характеристического уравнения будут равны:
вещественная и мнимая составляющие корней характеристического уравнения будут равны:  .
.
 , с частотой
, с частотой  , периодом
, периодом  и амплитудой
и амплитудой 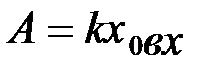 (рис. 2.15, б).
(рис. 2.15, б). и меньше
и меньше  , тем больше степень затухания колебательного звена. Следовательно, для уменьшения колебательности систем регулирования в колебательных звеньях необходимо увеличивать постоянную времени
, тем больше степень затухания колебательного звена. Следовательно, для уменьшения колебательности систем регулирования в колебательных звеньях необходимо увеличивать постоянную времени  и уменьшать
и уменьшать  . Однако это целесообразно делать лишь в определенных пределах, т.к. при чрезмерном увеличении отношения
. Однако это целесообразно делать лишь в определенных пределах, т.к. при чрезмерном увеличении отношения  переходный процесс затягивается. На рис. 2.16 приведен листинг Mathcad-программы расчета и построения графиков переходных процессов колебательных звеньев для различных отношений
переходный процесс затягивается. На рис. 2.16 приведен листинг Mathcad-программы расчета и построения графиков переходных процессов колебательных звеньев для различных отношений  .
.