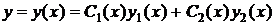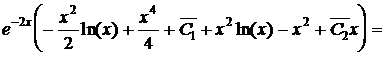Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Произвольных постоянных ЛагранжаРассмотрим уравнение вида
С учетом обозначения
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале (конечном или бесконечном). Теорема. Общее решение линейного неоднородного дифференциального уравнения Доказательство. Пусть Y – некоторое решение неоднородного уравнения. Тогда при подстановке этого решения в исходное уравнение получаем тождество:
Пусть
Далее покажем, что сумма
Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением. Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким-то образом отыскать одно частное решение неоднородного уравнения. На практике удобно применять метод вариации произвольных постоянных Лагранжа. Для этого сначала находят общее решение соответствующего однородного уравнения в виде:
Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:
Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:
Пример 1. Решить уравнение
Решение.  1) Решаем линейное однородное уравнение
2) Решение неоднородного уравнения будет иметь вид:
Составляем систему уравнений:
Решим эту систему:
Из соотношения
Теперь находим В(х).
Подставляем полученные значения в формулу общего решения неоднородного уравнения:
Окончательный ответ: Таким образом, удалось избежать нахождения частного решения неоднородного уравнения методом подбора. Пример 2. Найти общее решение . (10.1) Решение: 1) Сначала найдем общее решение
Характеристическое уравнение для уравнения (10.2) имеет вид
2) Перейдем к нахождению общего решения
Составляем вспомогательные определители
Теперь находим искомые функции
Определив функции
Ответ: Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.
Лекция 8 Линейные неоднородные дифференциальные уравнения с постоянными Коэффициентами. Уравнения с правой частью специального вида. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 207. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

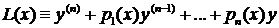 можно записать:
можно записать: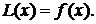
 в некоторой области есть сумма любого его частного решения и общего решения соответствующего линейного однородного дифференциального уравнения.
в некоторой области есть сумма любого его частного решения и общего решения соответствующего линейного однородного дифференциального уравнения.
 - фундаментальная система решений линейного однородного уравнения
- фундаментальная система решений линейного однородного уравнения  . Тогда общее решение однородного уравнения можно записать в виде:
. Тогда общее решение однородного уравнения можно записать в виде:
 является общим решением неоднородного уравнения.
является общим решением неоднородного уравнения.


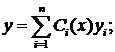
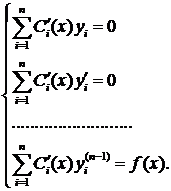




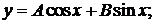



 найдем функцию А(х).
найдем функцию А(х).

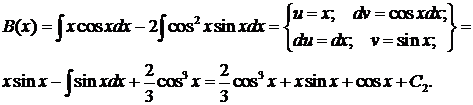

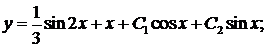

 для соответствующего ЛОДУ–II c постоянными коэффициентами
для соответствующего ЛОДУ–II c постоянными коэффициентами . (10.2)
. (10.2) . Его корни совпавшие
. Его корни совпавшие  . Тогда частные решения
. Тогда частные решения  ,
,  и общее решение
и общее решение  , , (10.3)
, , (10.3) (
(  ). (10.4)
). (10.4) ). Предварительно находим производные от частных решений
). Предварительно находим производные от частных решений 
 :
:
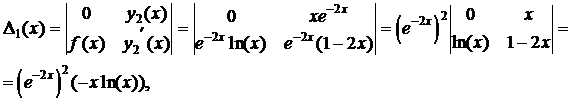

 :
: