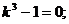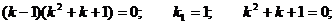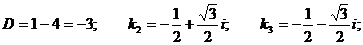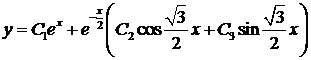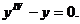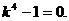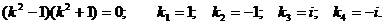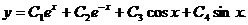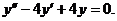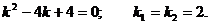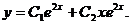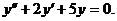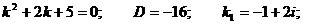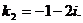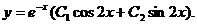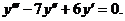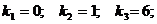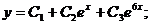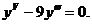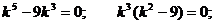Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные дифференциальные уравненияС постоянными коэффициентами Решение дифференциального уравнения вида
или, короче,
где k = const. Т.к.
При этом многочлен Для того, чтобы функция
Т.к. ekx ¹ 0, то Как и любое алгебраическое уравнение степени n, характеристическое уравнение В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные. Не будем подробно рассматривать каждый случай, а сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами. 1) Составляем характеристическое уравнение и находим его корни. 2) Находим частные решения дифференциального уравнения, причем: a) каждому действительному корню соответствует решение ekx; б) каждому действительному корню кратности m ставится в соответствие m решений: в) каждой паре комплексно-сопряженных корней г) каждой паре m – кратных комплексно – сопряженных корней  3) Составляем линейную комбинацию найденных решений. Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами. Пример 1. Решить уравнение
Решение. Составим характеристическое уравнение:
Общее решение имеет вид: Пример 2. Решить уравнение
Решение.Составим характеристическое уравнение:
Общее решение: Пример 3. Решить уравнение
Решение. Характеристическое уравнение: Общее решение: Пример 4. Решить уравнение
Решение.Характеристическое уравнение:
Общее решение: Пример 5. Решить уравнение
Решение.Характеристическое уравнение:
Общее решение: Пример 6. Решить уравнение
Решение.Характеристическое уравнение:
Общее решение:
Лекция 7 Линейные неоднородные дифференциальные уравнения С произвольными коэффициентами. Метод вариации |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 207. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

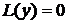 будем искать в виде
будем искать в виде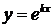 ,
, то
то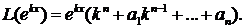
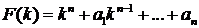 называется характеристическим многочленомдифференциального уравнения.
называется характеристическим многочленомдифференциального уравнения.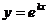 являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы
являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы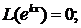 т.е.
т.е. 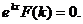
 - это уравнение называется характеристическим уравнением.
- это уравнение называется характеристическим уравнением.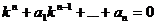 имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.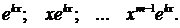
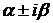 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения: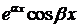 и
и 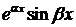 .
.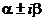 характеристического уравнения ставится в соответствие 2m решений:
характеристического уравнения ставится в соответствие 2m решений: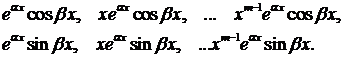
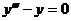 .
.