
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Однородные дифференциальные уравненияРассмотрим следующий тип дифференциальных уравнений первого порядка – однородные дифференциальные уравнения. Большинство однородных дифференциальных уравнений не являются уравнениями с разделяющимися переменными. Однако в ходе их решения приходится применять метод разделения переменных. Определение 4.1. Функция
Например, Аналогично проверяется, что функция Определение 4.2. Дифференциальное уравнение 1-го порядка вида
называется однородным дифференциальным уравнением, если функция Решение
где
Полученное последнее уравнение является дифференциальным уравнением с разделяющимися переменными. Разделяя переменные в нем, имеем Предполагая, что интеграл 
где обозначено Не стоит забывать, что при решении однородных уравнений необходимо проверять, являются ли Пример 4.1. Найти решение уравнения Решение: В данном случае функция
Решение отыскиваем в виде (4.3)
Получили дифференциальное уравнение с разделяющимися переменными; разделим переменные и проинтегрируем обе части. Получим
Итак, получили общее решение в виде Дифференциальное уравнение вида
является однородным, если функции Действительно, переписав уравнение (4.5) в виде Пример 4.2. Решить уравнение Решение: Первоначально заметим, что
причем уравнение (4.6) будем решать при условии, что Итак, решаем уравнение (4.6). Учитывая, как и прежде, что
Последнее полученное уравнение является дифференциальным уравнением с разделяющимися переменными. Решая его выше рассмотренным способом, получим Вычислим интеграл
Лекция 3 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 205. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 двух переменных
двух переменных  называется однородной функцией
называется однородной функцией  -го порядка, если при всех действительных
-го порядка, если при всех действительных  выполняется тождественно равенство
выполняется тождественно равенство . (4.1)
. (4.1)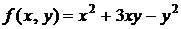 – однородная функция 2-го порядка, так как
– однородная функция 2-го порядка, так как  .
. является однородной функцией 1-го порядка, а функция
является однородной функцией 1-го порядка, а функция  – однородной функцией нулевого порядка. Далее везде в этом параграфе будем рассматривать только однородные функции нулевого порядка, то есть такие функции, для которых
– однородной функцией нулевого порядка. Далее везде в этом параграфе будем рассматривать только однородные функции нулевого порядка, то есть такие функции, для которых  .
. (4.2)
(4.2) уравнения (4.2) будем искать в виде
уравнения (4.2) будем искать в виде , (4.3)
, (4.3) – неизвестная функция. Дифференцируя искомое решение (4.3), и подставляя его в уравнение (4.2), получим
– неизвестная функция. Дифференцируя искомое решение (4.3), и подставляя его в уравнение (4.2), получим  ,
,

 по переменной u вычисляется конечным числом операций, получим общее решение (общий интеграл) уравнения (4.2) в виде
по переменной u вычисляется конечным числом операций, получим общее решение (общий интеграл) уравнения (4.2) в виде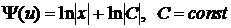 , (4.4)
, (4.4)
 .
.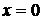 (то есть y = 0) и функция, которая получается при решении уравнения
(то есть y = 0) и функция, которая получается при решении уравнения  , частными решениями уравнения (4.2).
, частными решениями уравнения (4.2). .
. . Уравнение является однородным, так как функция
. Уравнение является однородным, так как функция 
 .
. , получим (подставляем в правую и левую части исходного дифференциального уравнения)
, получим (подставляем в правую и левую части исходного дифференциального уравнения)

 .
.

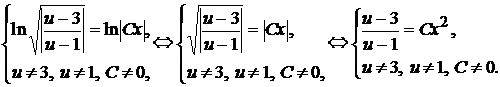
 , где
, где  . Осталось выяснить, являются ли функции
. Осталось выяснить, являются ли функции  ,
,  – частными решениями однородного уравнения. Убеждаемся в этом прямой подстановкой этих функций в дифференциальное уравнение.
– частными решениями однородного уравнения. Убеждаемся в этом прямой подстановкой этих функций в дифференциальное уравнение. (4.5)
(4.5) являются однородными функциями одного и того же порядка m.
являются однородными функциями одного и того же порядка m. , получим, что функция
, получим, что функция  является однородной нулевого порядка:
является однородной нулевого порядка: 
 .
. ,
,  – однородные функции 2-го порядка. Исходное уравнение является однородным. Переписав его в нужном для дальнейшего исследования виде, получим
– однородные функции 2-го порядка. Исходное уравнение является однородным. Переписав его в нужном для дальнейшего исследования виде, получим , (4.6)
, (4.6) , то есть
, то есть  . Сразу заметим, что функция x=0 является частным решением исходного дифференциального уравнения (подтверждается подстановкой), а функция
. Сразу заметим, что функция x=0 является частным решением исходного дифференциального уравнения (подтверждается подстановкой), а функция  – нет.
– нет. ,
, 




 Тогда общее решение нашего уравнения имеет вид
Тогда общее решение нашего уравнения имеет вид 