
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Допускающие понижение порядкаОпределение. Дифференциальным уравнением порядка n называется уравнение вида:
В некоторых случаях это уравнение можно разрешить относительно y(n):
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Определение. Решение
Определение. Нахождение решения уравнения Теорема Коши. (о необходимых и достаточных условиях существования решения задачи Коши). Если функция (n-1) –й переменных вида Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов. Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
7.1. Уравнения вида Рассмотрим сначала уравнение n-го порядка вида
где Общее решение уравнения (7.1) может быть получено путем n последовательных интегрирований ,
причем оно будет зависеть от n констант  Пример 7.1. Найти общее решение уравнения Решение: В данном случае (см. (7.1)) n = 3,
Ответ: Пример 7.2. Решить задачу Коши Решение: Имеем (см. (7.1)) n = 2, На первом шаге (интегрируя по частям)
и, учитывая, что
На втором шаге (интегрируя по частям)
учитывая, что
Уравнения вида Рассмотрим дифференциальное уравнение n-го порядка вида
не содержащее искомой функции Уравнение (7.2) введением новой функции
(
где неизвестной является функция Найдя решение уравнения (7.4) – функцию
относительно неизвестной функции В частном случае, когда n=2 дифференциальное уравнение (7.2) является уравнением второго порядка Пример 7.3. Найти общее решение уравнения
Решение: Представленное уравнение (7.6) является дифференциальным уравнением третьего порядка (n=3), которое можно записать в виде (7.2)
Заменой
с разделяющимися переменными относительно функции
Учитывая, что
Ответ: Пример 7.4. Найти общее решение уравнения
Решение: Уравнение (7.8) является дифференциальным уравнением второго порядка (n=2),
Разрешив это уравнение относительно своей производной, получим
Уравнение (7.9), очевидно, является однородным дифференциальным уравнением (функция
Учитывая, что
Последнее уравнение – уравнение с разделяющимися переменными:
Таким образом, общее решение уравнения (7.9) имеет вид
Непосредственно проверяется, что при
Теперь, исходя из равенства
Ответ:
7.3. Уравнения вида Рассмотрим дифференциальное уравнение второго порядка вида
относительно искомой функции Чтобы решить уравнение (7.12) вводят новую функцию
причем ее считают функцией аргумента Применяя теорему для производной сложной функции
Итак, замена (7.13) и выражение (7.14) приводят уравнение (7.12) к следующему виду
Уравнение (7.15) является дифференциальным уравнением первого порядка, в котором неизвестной функцией является функция Найдя решение уравнения (7.15), находят искомое решение
Пример 7.5. Найти частное решение уравнения
удовлетворяющее условию Решение: Представленное уравнение имеет вид (7.12), в котором
1) Вводим функцию
Для определения константы 2) Пользуясь равенством
Определим теперь значение константы Ответ: Лекция 6 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 249. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 удовлетворяет начальным условиям
удовлетворяет начальным условиям  , если
, если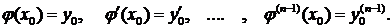
 в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по
в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по  , то какова бы не была точка (
, то какова бы не была точка (  ) в этой области, существует единственное решение
) в этой области, существует единственное решение  уравнения
уравнения  , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям
, определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям 
 – непрерывная функция,
– непрерывная функция,  .
.
 ,
, .
. .
. . Определим последовательно функции
. Определим последовательно функции  . Получим
. Получим



 ,
, 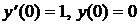 .
. . Последовательно находим функции
. Последовательно находим функции  , на каждом шаге определяя константы из условий
, на каждом шаге определяя константы из условий 
 , находим константу С1:
, находим константу С1: 

 , находим константу С2:
, находим константу С2:  Итак,
Итак,  – частное решение, удовлетворяющее условию
– частное решение, удовлетворяющее условию  , (7.2)
, (7.2) и ее производных до (
и ее производных до (  )-го порядка включительно (то есть функции
)-го порядка включительно (то есть функции  ).
). (7.3)
(7.3)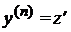 ) сводится к дифференциальному уравнению первого порядка
) сводится к дифференциальному уравнению первого порядка , (7.4)
, (7.4) (x – независимая переменная).
(x – независимая переменная). (7.5)
(7.5) . Тогда замена (7.3), которая здесь имеет вид
. Тогда замена (7.3), которая здесь имеет вид  , также приводит уравнение (7.2) к дифференциальному уравнению первого порядка (7.4).
, также приводит уравнение (7.2) к дифференциальному уравнению первого порядка (7.4). . (7.6)
. (7.6) .
. уравнение (7.6) приводится к уравнению
уравнение (7.6) приводится к уравнению (7.7)
(7.7)
 При
При 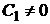 получили
получили  . Однако
. Однако  является частным решением уравнения (7.7). Тогда общее решение уравнения (7.7) можно записать в виде
является частным решением уравнения (7.7). Тогда общее решение уравнения (7.7) можно записать в виде  (частное решение
(частное решение  ).
). , находим последовательно функции
, находим последовательно функции 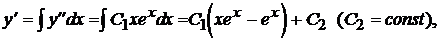


 . (7.8)
. (7.8)
 . Примем
. Примем  и уравнение (7.8) примет вид
и уравнение (7.8) примет вид .
. . (7.9)
. (7.9) – однородная нулевого порядка (проверьте!)). Решение уравнения (7.9) ищем в виде
– однородная нулевого порядка (проверьте!)). Решение уравнения (7.9) ищем в виде ,
,  .
. , получим
, получим .
.
 . (7.10)
. (7.10) функция
функция  не является частным решением уравнения (7.9), а при
не является частным решением уравнения (7.9), а при  функция
функция  является частным решением уравнения (7.9). Тогда общее решение уравнения (7.9) можно записать в виде
является частным решением уравнения (7.9). Тогда общее решение уравнения (7.9) можно записать в виде . (7.11)
. (7.11) , нетрудно найти общее решение исходного уравнения (7.8)
, нетрудно найти общее решение исходного уравнения (7.8)
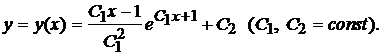

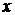 (
(  ).
).
 , (7.13)
, (7.13) !
! , найдем выражение для производной функции
, найдем выражение для производной функции 
 . (7.14)
. (7.14)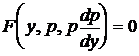 . (7.15)
. (7.15) .
. , (7.16)
, (7.16) .
. .
. , для которой
, для которой  . Уравнение (7.16) примет вид уравнения первого порядка
. Уравнение (7.16) примет вид уравнения первого порядка  с разделяющимися переменными относительно функции
с разделяющимися переменными относительно функции  .
. воспользуемся условиями
воспользуемся условиями  подставляем
подставляем  ,
,  :
: 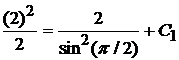 , откуда
, откуда  или
или  .
. .
. , воспользовавшись условием
, воспользовавшись условием  . Подставляя в равенство
. Подставляя в равенство  значения
значения  , получим
, получим  , если в явном виде, функция
, если в явном виде, функция  .
.