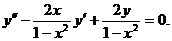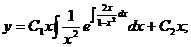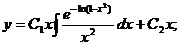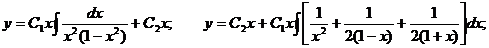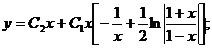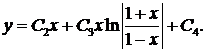Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные дифференциальные уравненияС произвольными коэффициентами. Структура общего решения Определение. Линейным дифференциальным уравнением n–го порядка называется любое уравнение первой степени относительно функции у и ее производных
где p0, p1, …,pn – функции от х или постоянные величины, причем p0 ¹ 0. Левую часть этого уравнения обозначим L(y).
Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однороднымуравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p0, p1, p2, … pn – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами. Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным. Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков. Рассмотрим уравнение вида
Определение. Выражение
называется линейным дифференциальным оператором. Линейный дифференциальный оператор обладает следующими свойствами:  1) 2) Решения линейного однородного уравнения обладают следующими свойствами: 1) Если функция у1 является решением уравнения, то функция Су1, где С – постоянное число, также является его решением. 2) Если функции у1 и у2 являются решениями уравнения, то у1 +у2 также является его решением.
Структура общего решения Определение. Фундаментальной системой решенийлинейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения. Определение. Если из функций yi составить определитель n – го порядка
то этот определитель называется определителем Вронского. (Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик) Теорема 1. Если функции Теорема 2. Если функции Теорема 3. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема 4. Если
где Ci –постоянные коэффициенты.
Общее решение линейного однородного дифференциального Уравнения второго порядка Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.Из вышеизложенного видно, что отыскание общего решения линейного однородного дифференциального уравнения сводится к нахождению его фундаментальной системы решений. Однако, даже для уравнения второго порядка, если коэффициенты р зависят от х, эта задача не может быть решена в общем виде. Тем не менее, если известно одно ненулевое частное решение, то задача может быть решена. Теорема 5. Если задано уравнение вида
Таким образом, для получения общего решения надо подобрать какое-либо частное решение дифференциального уравнения, хотя это бывает часто довольно сложно. Пример. Решить уравнение Решение. Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое-либо частное решение. Таким частным решением будет являться функция
Исходное дифференциальное уравнение можно преобразовать:
Общее решение имеет вид:
Окончательно:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 205. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 вида:
вида: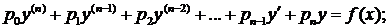
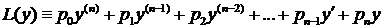 .
.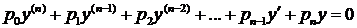
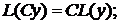
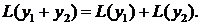
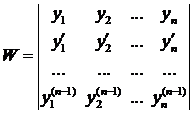 ,
, линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю.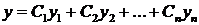 ,
,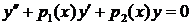 и известно одно ненулевое решение у = у1, то общее решение может быть найдено по формуле:
и известно одно ненулевое решение у = у1, то общее решение может быть найдено по формуле: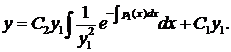
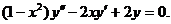
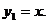 Действительно,
Действительно,