
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод вариации произвольного постоянного ЛагранжаРассмотрим другой метод нахождения общего решения уравнения (5.2), называемый методом вариации произвольного постоянного Лагранжа. Определение 5.2. Пусть дано уравнение (5.2). Уравнение с правой частью
Метод нахождения общего решения уравнения (5.2) основан на знании общего решения соответствующего однородного (5.8) и состоит из двух этапов. На первом этапе ищут общее решение
На втором этапе ищут общее решение исходного уравнения в виде
где Пример 2. Найти методом вариации произвольного постоянного Лагранжа частное решение ЛДУ-I
удовлетворяющее начальному условию Решение: Сначала найдем общее решение однородного уравнения  Имеем Итак, Теперь общее решение исходного уравнения (5.11) необходимо искать в виде
где функция исходное уравнение, получим
Найдем частное решение, удовлетворяющее начальному условию Ответ: Лекция 4 Уравнение Бернулли. Метод решения Определение. Уравнением Бернуллиназывается уравнение вида
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1. Для решения уравнения Бернулли применяют подстановку
с помощью которой уравнение Бернулли приводится к линейному. Для этого разделим исходное уравнение на yn.
Применим подстановку, учтя, что
Т.е. получилось линейное уравнение относительно неизвестной функции z. Решение этого уравнения будем искать в виде:
Пример. Решить уравнение Решение. Разделим уравнение на xy2:
Полагаем
Полагаем
Произведя обратную подстановку, получаем:
Пример. Решить уравнение Решение. Разделим обе части уравнения на
Полагаем
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
Получаем: Применяя обратную подстановку, получаем окончательный ответ:
Лекция 5 Дифференциальные уравнения высших порядков. Дифференциальные уравнения высших порядков, |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 208. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
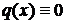 называется линейным однородным дифференциальным уравнением первого порядка, соответствующее ЛДУ-I. Оно имеет вид
называется линейным однородным дифференциальным уравнением первого порядка, соответствующее ЛДУ-I. Оно имеет вид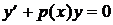 . (5.8)
. (5.8)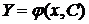 (
( 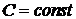 ) уравнения (5.8) (оно является уравнением с разделяющимися переменными). Найти его общее решение нетрудно:
) уравнения (5.8) (оно является уравнением с разделяющимися переменными). Найти его общее решение нетрудно: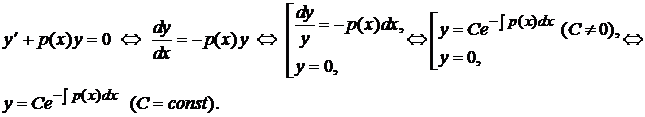 Итак, общее решение уравнения (5.8) имеет вид
Итак, общее решение уравнения (5.8) имеет вид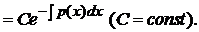 (5.9)
(5.9)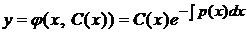 , (5.10)
, (5.10)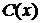 – неизвестная функция. Далее поступают знакомым приемом: предполагая, что общее решение уравнения (5.2) должно иметь вид (5.10), подставляют в левую часть (5.2) выражение (5.10) и выражение для ее производной
– неизвестная функция. Далее поступают знакомым приемом: предполагая, что общее решение уравнения (5.2) должно иметь вид (5.10), подставляют в левую часть (5.2) выражение (5.10) и выражение для ее производной 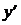 . При правильной такой подстановке получится равенство для определения неизвестной функции
. При правильной такой подстановке получится равенство для определения неизвестной функции  , (5.11)
, (5.11)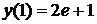 (решить задачу Коши).
(решить задачу Коши). , соответствующее уравнению (5.11).
, соответствующее уравнению (5.11).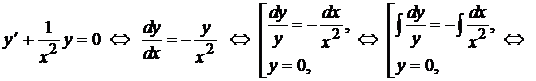
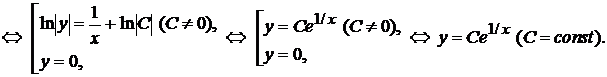
 есть общее решение линейного однородного, соответствующего (5.11).
есть общее решение линейного однородного, соответствующего (5.11). , (5.12)
, (5.12)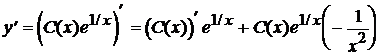 ) и используя
) и используя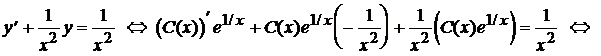
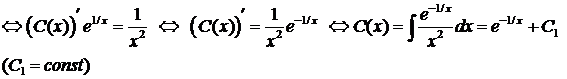 Итак, функция
Итак, функция 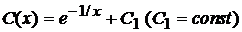 . Согласно равенству (5.12) общее решение уравнения (7.3.11) имеет вид
. Согласно равенству (5.12) общее решение уравнения (7.3.11) имеет вид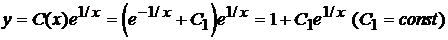 . (5.13)
. (5.13) в общем решении (5.13). Подставляя в равенство (5.13)
в общем решении (5.13). Подставляя в равенство (5.13) 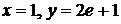 , получим
, получим 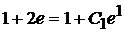 , откуда
, откуда 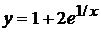 ,
, 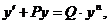
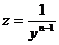 ,
,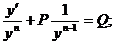
 .
.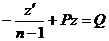
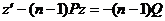
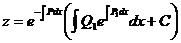 .
.
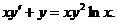
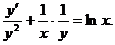
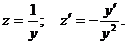 Тогда
Тогда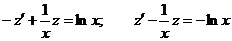 .
.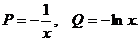
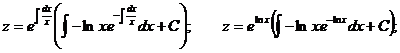
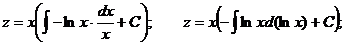
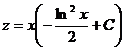 .
.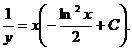
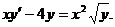
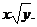
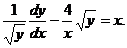
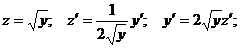
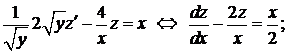
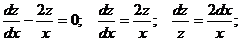
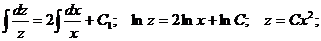
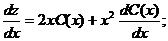


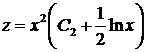 .
. .
.