
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ ЛИНЕЙНЫХ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮЦель работы: изучить влияние обратной связи на устойчивость линейных систем. Теоретические сведения
Одноконтурная система с обратной связью может быть представлена в виде некоторой структурной схемы (рис.8)
Рис.8 Структурная схема одноконтурной системы с обратной связью
W(s) – передаточная функция прямой цепи; Woc(s) – передаточная функция обратной цепи; x(t) – входной сигнал; y(t) – выходной сигнал; r(t) – сигнал обратной связи;
В результате охвата обратной связью входной сигнал x(t) складывается с сигналом обратной связи r(t) и вызывает некоторую реакцию y(t). Соотношение между изображениями входного сигнала и реакции на него получается:
следовательно передаточная функция для замкнутой системы будет иметь следующий вид:
+ - ставится при отрицательной обратной связи; - - ставится при положительной обратной связи. Даже если прямая и обратная цепи будут линейно устойчивы, часто бывают случаи, что получившаяся система с обратной связью часто становится неустойчивой как при положительной, так и при отрицательной обратной связи (термины отрицательная и положительная обратная связь употребляются для того, чтобы описать воздействие обратной связи по отношению к реакции системы). Между понятием отрицательной и положительной обратной связи нет четкой границы, так как одна и та же связь может быть отрицательной при одних частотах и положительной при других, что объясняется существованием разности фаз входного сигнала и сигнала обратной связи, поступающих на элемент сравнения, что обусловлено инерционностью отдельных элементов системы. По мере отклонения фазы сигнала обратной связи ее эффективность снижается. На практике это означает, что при замыкании обратной связи, сигналы в такой системе начинают самопроизвольно колебательно или апериодически возрастать. В силу физической природы элементов, процессы в системе никогда не могут неограниченно возрастать, они ограничиваются запасом энергии питания.  Введение обратной связи может преследовать две основные цели в зависимости от типа обратной связи: 1)положительная обратная связь используется для создания режимов автоколебаний, преимущественно в электронных схемах генераторов, и почти не используется в контурах САУ; 2)отрицательная обратная связь широко используется для стабилизации самых разных систем, в том числе при построении САУ. В последнем случае цель её введения - придать объекту управления некие желательные свойства, заставить его реагировать должным образом на входное воздействие и минимизировать или практически исключить влияние собственных шумов и нелинейностей объекта. Поэтому далее будут рассматриваться системы с отрицательной обратной связью. Неустойчивость систем с обратной связью впервые была исследована в 1868 г. Д. К. Максвеллом. Условие устойчивости любой системы состоит в том, чтобы корни знаменателя её передаточной функции не имели положительной действительной части, так как такие корни вызывают неустойчивость системы. Граничный случай получается, когда корни чисто мнимые. В случае замкнутых систем для знаменателя общей передаточной функции который может быть и обычно бывает 3-го и более высоких порядков отыскание корней становится очень непростой задачей. Между тем, для суждения об устойчивости системы знания точных значений этих корней не требуется. Достаточно уверенности в отсутствии корней с положительной действительной частью. Для решения этой задачи был разработан ряд критериев, к которым относятся критерий Рауса, Гурвица и критерий Михайлова [1,2,3]. Следует подчеркнуть, что эти критерии относятся к любым системам, описываемым передаточными функциями, — замкнутым и разомкнутым. Другой подход к исследованию устойчивости основан на критерии Найквиста [1,2,3], который позволяет судить об устойчивости замкнутой системы по передаточной функции разомкнутой системы. Критерий устойчивости Найквиста. Этот критерий разработан в 1932 г., американским ученым Г.Найквистом, и позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики. Наиболее наглядная и поддающаяся физической интерпретации оценка условий, необходимых для устойчивости линейных систем с обратной связью, получается при рассмотрении процесса возбуждения системы синусоидальными воздействиями, так как в этом случае процессы в линейной системе тоже будут синусоидальными. Пусть передаточная функция разомкнутой системы имеет следующий вид:
при подстановке s=jω получаем частотную передаточную функцию:
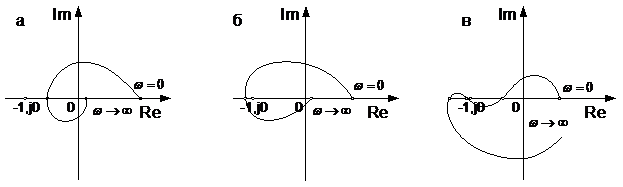
Если изменять частоту ω от – ∞ до +∞, то вектор W(jω) будет изменяться по величине и фазе. АЧХ получающуюся в результате называют также годографом, в данном случае годографом Найквиста. Критейрий устойчивости Найквиста гласит: Если разомкнутая система статическая и устойчивая, то необходимое и достаточное условие устойчивости замкнутой системы с передаточной функцией состоит в том, чтобы годограф при изменении частоты со от 0 до +со не охватывал начала координат комплексной плоскости, или, иначе говоря, годограф АФХ разомкнутой системы не охватывал точку с координатами Rе = -1, 1т = 0 на комплексной плоскости. Примеры годографов Найквиста разомкнутых устойчивых статических систем, образующих при замыкании как устойчивые рис.9а, так и неустойчивые замкнутые системы приведены на рис.9б. Особо интересным представляется годограф на рис.9в. Он соответствует условно устойчивой системе..
Рис. 9 Примеры годографов Найквиста
Использование ЛАЧХ и ФЧХ для анализа устойчивости. Если частотные характеристики разомкнутой системы известны и замкнутая система устойчива, то критерий Найквиста может быть применен в модифицированной форме, основанной не на анализе ведения годографов в комплексной плоскости, а на анализе ЛЧХ и ФЧХ. ЛЧХ и ФЧХ, как отмечалось выше, строятся по следующим выражениям:
Для устойчивости замкнутой системы требуется, чтобы дополнительный фазовый сдвиг в разомкнутой инвертирующей системе был меньше 1800 именно на частоте, где L(ω) = 1. Эта частота называется частотой срезаразомкнутой системы. Пример приведен на рис. 10 а,б, где показаны характеристики устойчивой и неустойчивой системы в замкнутом состоянии.
Рис.10 Примеры ЛАЧХ и ФЧХ разомкнутых систем.
На рис.11 приведены примеры ЛАЧХ и ФЧХ для системы находящейся на рис.11б границе колебательной устойчивости и для условно устойчивой системы
Рис.11 Примеры ЛАЧХ и ФЧХ разомкнутых систем.
Использование комплексных плоскостей с корнями характеристического уравнения для определения устойчивости переходного процесса.
Для определения устойчивости нет необходимости решать дифференциальное характеристическое уравнение и находить его корни. Характеристическим уравнением является знаменатель замкнутой передаточной функции:
Так как в решении характеристического уравнения содержаться n корней, то переходная составляющая может быть записана в виде:
где p1…pn - корни характеристического уравнения. Определим, какие свойства корней необходимы и достаточны для определения устойчивости динамической системы. Корни характеристического уравнения могут быть вещественными, мнимыми или комплексными.
1. Вещественный корень. Если один из корней p1 вещественный. При p1=-a1 , то слагаемое, определяемое этим корнем * будет представлять собой затухающую экспоненту
Рис.12 Вещественные корни 2. Комплексные корни. Как правило комплексные корни бывают попарно сопряженными. При отрицательной вещественной части два корня, например p1и p2 будут иметь вид р1,2=-a±jb. В этом случае слагаемые определяемые этими корнями могут быть представлены в виде:
где А и φ – новые постоянные интегрирования. Т.е. в этом случае появляются затухающие колебания (рис.13 )
Рис.13 Комплексные корни
При положительной вещественной части р1,2=+a±jb, колебания будут расходящимися (рис, 14). 3. Мнимые корни. В этом случае р1=+jb и р2=-jb . слагаемое определяемое этими корнями будут незатухающие колебания:
Рис. 14 Комплексные корни
Рис.15 Мнимые корни
Следовательно, для затухания переходного процесса необходимо, чтобы вещественные части корней были отрицательными. Это относится и к вещественным корням и к комплексным. Корни характеристического уравнения можно представить в виде точек на комплексной плоскости величины s. Для устойчивости линейной системы необходимо и достаточно, чтобы все корни лежали слева от мнимой оси плоскости корней. Если хотя бы один корень окажется справа, то система будет неустойчивой. Границей перехода будет граница устойчивой системы. Система будет находится на границе устойчивости при наличии: 1. Нулевого корня. 2. Пары чисто мнимых корней. 3. Бесконечно-большого корня.
Рис.16 Расположение корней на комплексной плоскости, а - пример устойчивой системы, б – пример неустойчивой системы
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 938. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


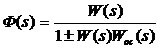

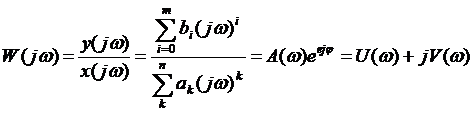



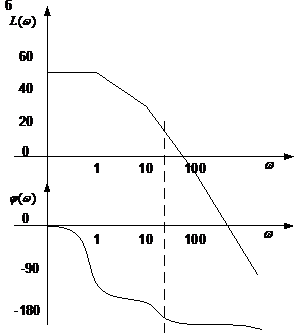



 *
*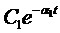 , в обратном случае расходящуюся (рис.12)
, в обратном случае расходящуюся (рис.12)


 (рис.15)
(рис.15)

