
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИЦель работы: ознакомление с методами построения переходных характеристик типовых динамических звеньев в системе имитационного моделирования CLASSIC, и ознакомление с методиками определения основных параметров типовых динамических звеньев по виду переходных характеристик.
Теоретические сведения Существует большое разнообразие автоматических систем, выполняющих различные функции по управлению физическими процессами во всех областях техники. В этих системах сочетаются весьма разнообразные по конструкции механические, электрические и другие устройства, составляя сложный комплекс взаимодействующих друг с другом звеньев. Такие звенья называются динамическими звеньями. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления, но описываемое определенным дифференциальным уравнением. В соответствии с этим классификация звеньев происходит по виду дифференциального уравнения или по виду передаточной функции (формулы). Передаточные функции, вводятся для сокращения записи дифференциальных уравнений и также представляют собой символическую запись дифференциальных уравнений.
1. Дифференциальное уравнение
где x(t) - входное воздействие; y(t) - выходной сигнал (управляемая переменная); an, an-1, … , a0, bm, bm-1, … , b0 - постоянные коэффициенты, определяемые физическими параметрами звена (системы);
2. Передаточная функция

где p - оператор; y(p) и x(p) - изображения y(t) и x(t) соответственно;
уравнение удобно записывать в символической форме, введя алгебраизированный оператор дифференцирования
3. Передаточная функция Лапласа
где s - оператор Лапласа; y(s) и x(s) - изображения по Лапласу y(t) и x(t) соответственно.
Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, гидравлические, электрические и т.д.). Для теории управления это будет один и тот же тип звена. Звенья бывают позиционные, дифференцирующие и интегрирующие. В звеньях позиционного типа связаны линейной зависимостью выходная и входная величина в установившемся режиме: x2=kx1 Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена. В звеньях интегрирующего типа линейной зависимостью связаны производная выходной величины и входная величина в установившемся режиме:
В этом случае для установившегося режима будет справедливо равенство:
Коэффициент пропорциональности k между выходной и входной величинами здесь также представляет собой коэффициент передачи звена. В звеньях дифференцирующего типа линейной зависимостью связаны в установившемся режиме выходная величина и производная входной:
Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена.
В таблице (1) приведены некоторые разновидности типовых динамических звеньев. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка
Таблица1
Динамические свойства звена могут быть определены по его переходной функции и функции веса. Реакция звена при подаче на его вход единичной ступенчатой функции называется переходной функцией, или переходной характеристикой, h(t) представляющей собой переходной процесс (на производстве разгонная характеристика) на его выходе. Ступенчатая функция (рис.2) является самым распространенным видом входного воздействия в автоматических системах. К такому виду сводятся мгновенное изменение нагрузки генератора, мгновенное возрастание нагрузки на валу двигателя и т.п.
Рис.2 Единичный ступенчатый сигнал
Если входное воздействие представляет собой неединичную ступенчатую функцию Реакция звена на единичную импульсную функцию (рис.3), поданную на его вход, называют функцией веса w(t), которая как бы определяет вес, с которым каждый входной импульс, полученный при разложении входного сигналу, участвует в формировании выходного сигнала в следующий момент времени.
Рис.3 Единичная импульсная функция
Основное свойство дельта-функции заключается в том, что:
т.е. она имеет единичную площадь. Для установления связи между переходной функцией и функцией веса рассмотрим входное воздействие звена в виде конечного по высоте и ширине импульса с площадью Ne=1, прикладываемого в момент времени t=0. Такой импульс можно представить двумя ступенчатыми функциями
Импульсная функция является также распространенным на практике видом входного воздействия (кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания и т. д.). По реакции динамической системы на ступенчатый сигнал можно определить ряд практически важных параметров. Все экспериментальные методы базируются на предположении о сосредоточенности параметров звена (системы), стационарности во времени его динамических свойств и их линейности при малых изменениях входных воздействий.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1033. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||
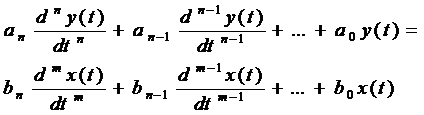




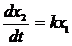













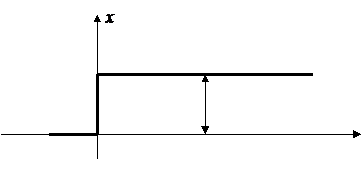
 , выходная величина будет равна
, выходная величина будет равна 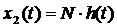 , в данном случае переходную характеристику определяем как отношение выходной величины звена x2(t) к высоте ступенчатого скачка
, в данном случае переходную характеристику определяем как отношение выходной величины звена x2(t) к высоте ступенчатого скачка  .
. Единичная импульсная функция (дельта-функция), представляет собой производную от единичной ступенчатой функции: d(t) = 1’(t). Дельта-функция тождественно равна нулю в любой токе, кроме точки t=0, где она стремится к бесконечности.
Единичная импульсная функция (дельта-функция), представляет собой производную от единичной ступенчатой функции: d(t) = 1’(t). Дельта-функция тождественно равна нулю в любой токе, кроме точки t=0, где она стремится к бесконечности. ,
, и
и  , прикладываемыми ко входу звена со сдвигом во времени e. После преобразований получим:
, прикладываемыми ко входу звена со сдвигом во времени e. После преобразований получим: