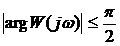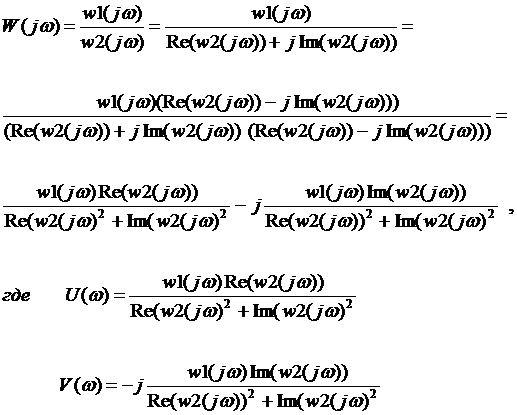Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
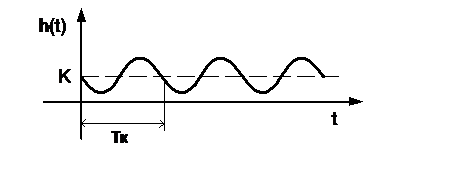
Определение параметров динамических звеньев по временным характеристикамПо реакции динамической системы на ступенчатый сигнал можно определить ряд практически важных параметров. При подборе параметров модели К и Т по переходным характеристикам реального объекта высокого порядка стремятся это сделать так, чтобы лучшим образом приблизить аппроксимирующую переходную характеристику к действительной. Одним из решений этой задачи является графический способ определения параметров динамических звеньев (таблица 2).
Таблица 2
Задание на лабораторную работу
1. По структурной схеме (рис.4) построить схему моделирования в системе CLASSIC.
Рис.4 Структурная схема
2. Построить переходные процессы для следующих типовых динамических звеньев: пропорционального, интегрального, интегрального с замедлением, апериодического первого порядка, апериодического второго порядка, колебательного, дифференциального.(данные коэффициентов К и постоянных времени Т, для типовых динамических звеньев, брать, в соответствии с вариантом, из таблицы x=0.01). Переходные процессы построить дважды для различных значений Т и К.
Таблица 3
3. Зарисовать полученные в ходе эксперимента переходные характеристики с нанесенными масштабами, обозначениями и соответствующими исходными данными.  4. Полученные таким образом переходные процессы необходимо сравнить и сделать необходимые выводы о влиянии на вид переходного процесса постоянных времени Т и коэффициентов усиления К 5. Определить графоаналитическим методом по экспериментальным переходным характеристикам параметры передаточных функций типовых динамических звеньев.
Содержание отчета 1. Название работы, цель. 2. Структурную схему моделирования. 3. Преобразованную схему моделирования. 4. Рисунки полученных графиков переходного процесса, численные значения постоянных времени Т и коэффициентов усиления К , определенных графоаналитическим методом. 5. Необходимые выводы.
Контрольные вопросы
1. Какие воздействия являются типовыми? 2. Что такое переходной процесс? 3. Какие вы знаете временные характеристики? 4. Начертите переходные процессы типовых динамических звеньев? 5. Что такое весовая функция? 6. Как связаны между собой весовая и переходная функции? 7. Как определить постоянную времени Т и коэффициент усиления К по переходной характеристике? 8. Что такое коэффициент передачи? 9. Что такое переходный процесс?
Лабораторная работа №3
ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ДИНАМИЧЕСКИХ ЗВЕНЬЕВ Цель работы: ознакомление с методами построения частотных характеристик линейных динамических звеньев в том числе при помощи системы имитационного моделирования CLASSIC.
Теоретические сведения Важнейшими характеристиками динамические звеньев являются их частотные характеристики. Для их получения необходимо на вход динамической системы подать гармонический сигнал, при нулевых начальных условиях. Существует однозначная связь между частотной характеристикой системы в установившемся состоянии и всеми другими видами ее описания. Другое важное преимущество частотных методов состоит в том, что сами частотные характеристики могут быть достаточно легко непосредственно измерены или построены из аналитических выражений. Одной из частотных характеристик является ее частотная передаточная функция. Если передаточная функция системы по определению:
То функцию W(jω), получают из передаточной функции при подстановке s=jω:
Частотная передаточная функция есть изображение Фурье его функции веса, и следовательно должна быть представлена в следующем виде:
где А(ω) – модуль частотной передаточной функции; φ(ω) –аргумент или фаза; U(ω) и V(ω) – вещественная и мнимая составляющие частотной передаточной функции. Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя:
Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя:
Для определения мнимой и действительной частей частотной передаточной функции необходимо освободиться от мнимости путем умножения числителя на комплексную сопряженную знаменателю величину, а затем произвести разделение мнимой и действительной части.
Для анализа частотных свойств динамической системы звена, в зависимости от задач, используются различные частотные характеристики.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 517. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

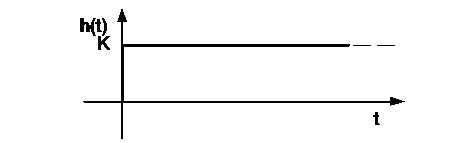
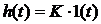


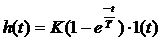


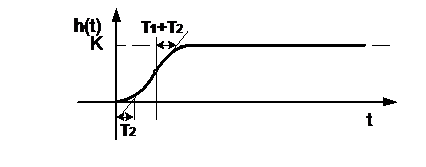
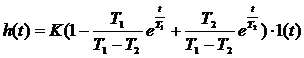


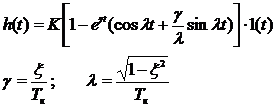
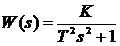
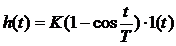


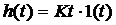


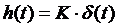

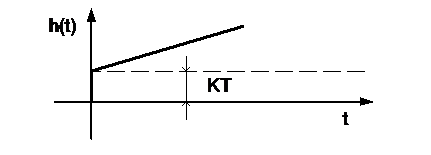
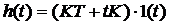

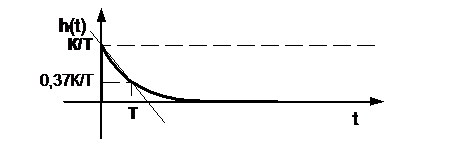
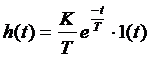


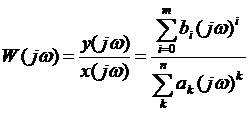
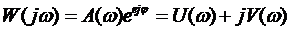 ,
,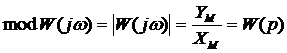
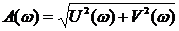
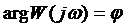
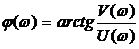 , если
, если