
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения Гамильтона, или канонические.Уравнения Лагранжа (3.8) представляют собой систему обыкновенных дифференциальных уравнений второго порядка относительно обобщенных координат qt. Число уравнений равно числу степеней свободы s. Известно, что порядок дифференциальных уравнений можно понизить путем введения новых переменных и увеличением количества уравнений. В классической механике в качестве дополнительного набора переменных выбирают обобщенные импульсы
Для замены переменных в уравнениях Лагранжа используется известное в теории дифференциальных уравнений преобразование Лежандра. В данном случае для этого запишем дифференциал функции Лагранжа как функции переменных
Используя тождество преобразуем равенство (7.2) к виду
В левой части формулы (7.3) стоит дифференциал от полной энергии механической системы (3.39), взятый со знаком минус. Для того чтобы использовать равенство (7.3), необходимо энергию записать как функцию переменных qi, рi и t, дифференциалы которых стоят в правой части равенства (7.3). Энергия механической системы, выраженная через обобщенные координаты, обобщенные импульсы и время, играет важную роль в механике. Она называется функцией Гамильтона и обозначается буквой Н:
Из формулы (7.3) и определения дифференциала Н как функции переменных qi, рi и t получаем следующие выражения для частных производных от функции Гамильтона: Первое из равенств (7.5) является соотношением, обратным определению обобщенного импульса (7.1), так как позволяет выразить обобщенные скорости q\ через обобщенные импульсы рi. С помощью второго равенства из (7.5) производные от функции Лагранжа по координатам в уравнении Лагранжа можно заменить на производные от функции Гамильтона. Производя эту замену в уравнениях Лагранжа, записанных согласно (3.35) через обобщенные импульсы, и добавляя к полученным уравнениям первое из равенств (7.5), получаем систему уравнений: 
Уравнения (7.6) называются уравнениями Гамильтона. Это система дифференциальных уравнений первого порядка относительно удвоенного набора неизвестных q{ и р,-. Число уравнений в два раза больше числа уравнений Лагранжа и равно 2s. Как и уравнения Лагранжа, уравнения Гамильтона получаются из одной скалярной функции — функции Гамильтона. Преимуществом системы (7.6) является еще и то, что уравнения разрешены относительно производных от координат и импульсов. Вследствие простоты уравнений Гамильтона их также называют каноническими уравнениями механики.
Канонические уравнения можно получить из модифицированного принципа наименьшего действия. Для этого из определения (7.4) выразим функцию Лагранжа через функцию Гамильтона и полученное выражение подставим в интеграл действия (2.22). В результате действие приводится к виду
Считая в выражении (7.7) обобщенные координаты и обобщенные импульсы независимыми переменными, запишем вариацию действия Разобьем интеграп на сумму нескольких интегралов. Во втором интеграле выполним интегрирование по частям. Как и при выводе уравнений Лагранжа, используем перестановочность операций варьирования и дифференцирования. Записывая опять все под одним интегралом, в результате получим Поскольк чтобы вариация действия обращалась в нуль, следуют равенства
После деления их на dt получим канонические уравнения (7.6). Таким образом канонические уравнения выводятся из принципа наименьшею действия, если действие представить в виде (7.7). В качестве примера рассмотрим получение функции Гамильтона и канонических уравнений в полярной системе координат для материальной точки, движущейся в плоскости. Функция Лагранжа для этой задачи приведена в формуле (3.18). Найдем для нее обобщенные импульсы:
Запишем энергию системы и с помощью формул (7.11) выразим ее через обобщенные импульсы. В результате получим функцию Гамильтона Теперь вычисляем производные от функции Гамильтона:
Значения производных подставляем в формулы (7.6) и получаем канонические уравнения в полярных координатах:
|
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 760. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (7.1)
(7.1)


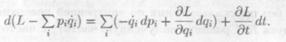 (7.3)
(7.3) (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8) (7.9)
(7.9) независимые вариации, то из требования,
независимые вариации, то из требования, (7.10)
(7.10) (7.11)
(7.11) (7.12)
(7.12) (7.13)
(7.13) (7.14)
(7.14)