
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчёт на прочность при косом изгибе.Для оценки прочности конструкции необходимо определить опасное сечение. Там где одновременно возникают наибольшие изгибающие моменты. Затем в этом сечении находят опасные точки. Там где возникают наибольшие нормальные напряжения. 1) Для поперечных сечений произвольной формы для определения опасных точек необходимо знать положение нейтральной линии. Она проходит через точки где нормальные напряжения равны 0. Приравняем нормальное напряжение к 0 σ= Полученное выражение показывает что нулевая линия представляет собой прямую, проходящею через начало координат( центр тяжести сечения)и наклонена к оси X под углом tgφ=--
В этой формуле учитываются знаки изгибающих моментов. При данном загружении φ<0. С другой стороны Tgφ= В симметричных сечениях условие прочности имеет вид 
Определение деформаций при косом изгибе Деформации при косом изгибе определяют на основе принципа независимости действия сил, путём геометрического суммирования прогибов, полученных в направлении главных осей. Для бруса защемлённого одним концом и нагруженного силой на свободном конце используя справочные формулы получим
Полный прогиб V= Рисунок Найдём направление полного прогиба tgΨ=
Где Ψ- угол между направлением полного прогиба и осью Y При косом изгибе направление полного прогиба перпендикулярно нейтральной линии. Tgφ= Растяжение-сжатие с изгибом. Внутренние силы. Напряжение. Рисунок
В общем случае при данном виде деформации возникает пять внутренних сил: Продольная сила –N Поперечные силы Изгибающий момент Напряжение определяют отдельно от каждой внутренней силы и суммируется σ=± Если материал не одинаково сопротивляется растяжению-сжатию, то записывают две формулы Нецентренное растяж,сжатие Возник,когда на элемент конструкции действ сила или равнодей-щая сил по прямой, ll-ной его продольной оси, но не совпадающая с ней.Рис.
Xf,Yf-точки прилож силы в глав центр осях Силу F переносим в ц.т. сечения. В результате получаем сжимающую силу F и 2 момента-Mx и My. Внутренние силы будут равны N=-F(тк сжим).
При нецентр растяж-сжат все сеч-ия равноопасны и эпюры внутр сил строить не обязательно. Нормальное напряж в любой точке попер сечения Сигма=+ - N/A+ - Mx*Y/Ix+ -My*x/Iy (1) X и Y-коорд точек, в котор опред напряж в глав центр осях.Знак слагаемых выбира по харак деформ в точке. Если точка от вну силы сжим –, если растяж +. Формулы: Для внецентр Растяж: Сигма=(1)=F/A+ F*Yf*Y/Ix+F*Xf*X/Iy Сиг=F(1/A + Yf*Y/Ix + Xf*X/Iy) Для внецентр сжат: Сиг=- F(1/A + Yf*Y/Ix + Xf*X/Iy) Величины корд подстав со своими знаками
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 541. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
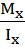 Y+
Y+  X=0 Y=-
X=0 Y=-  X
X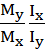 Если φ>0 то откладывают его от оси Х против часовой стрелки, если φ<0 то по часовой. РИСУНОК
Если φ>0 то откладывают его от оси Х против часовой стрелки, если φ<0 то по часовой. РИСУНОК *
*  =
=  . В отличии от плоского изгиба нейтральная линия не перпендикулярна силовой линии. Исключением является круг, квадрат у которых
. В отличии от плоского изгиба нейтральная линия не перпендикулярна силовой линии. Исключением является круг, квадрат у которых  . Следовательно φ=α – плоский изгиб. Вывод: Для сечений типа круг и квадрат, и т.д. у которых все центральные оси главные, косой изгиб невозможен . Если найдено положение нейтральной оси, то наибольшее напряжение возникает в точках, наиболее удаленных от неё. A и B—опасные точки. Для сечений произвольной формы условие прочности имеет вид:
. Следовательно φ=α – плоский изгиб. Вывод: Для сечений типа круг и квадрат, и т.д. у которых все центральные оси главные, косой изгиб невозможен . Если найдено положение нейтральной оси, то наибольшее напряжение возникает в точках, наиболее удаленных от неё. A и B—опасные точки. Для сечений произвольной формы условие прочности имеет вид:  =
=  +
+  ≤R где
≤R где  и
и  —координаты опасных точек в главных центральных осях.
—координаты опасных точек в главных центральных осях. +
+  ≤R где
≤R где 
 =
= 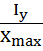 . В данных сечениях положение нейтральной линии находить необязательно. Наибольшие напряжения возникают в угловых точках. Если материал неодинаково сопротивляется растяжению-сжатию, то записывается два условия прочности. Отдельно для растянутой зоны, отдельно для сжатой.
. В данных сечениях положение нейтральной линии находить необязательно. Наибольшие напряжения возникают в угловых точках. Если материал неодинаково сопротивляется растяжению-сжатию, то записывается два условия прочности. Отдельно для растянутой зоны, отдельно для сжатой.  ≤
≤ 
 ≤
≤ 
 =
= 
 =
=  Рисунок
Рисунок =
= 


 =
=  tgα
tgα 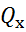



 ±
±  ±
± 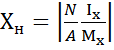
 Нейтральная линия делит сечение на две части: растянутую и сжатую. Опасными в сечении являются точки наиболее удаленные от нейтральной линии. Основной расчётной формулой является условие прочности
Нейтральная линия делит сечение на две части: растянутую и сжатую. Опасными в сечении являются точки наиболее удаленные от нейтральной линии. Основной расчётной формулой является условие прочности 
 ≤
≤ 
 ≤
≤ 

 Эпюры внутр сил Mx=F*Yf (Yf-расст до оси X), My=F*Xf. Рис.
Эпюры внутр сил Mx=F*Yf (Yf-расст до оси X), My=F*Xf. Рис.