
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение перемещений методом непосредственного интегрирования диф-ого уравнения.Стр 1 из 15Следующая ⇒ Полная проверка прочности балки при изгибе. Как показал опыт эксплуатации изгибаемых элементов конструкций, разрушение их начинается с крайних волокон, где возникают наибольшие норм.напряжения Вычисляем главное напряж. для целого ряда точек по высоте сечения можно построить эпюры δ1 и δ3 . Зачастую скачки на эпюрах δ1 δ 3 превышают δ max.Поэтому возник.необходимость полной проверки прочности балки 1) По нормальным напряжениям в сечении где возникает наиб.изгибающий момент: δ 2) По касат. напряжению в сечении где возникает наибольшая поперечная сила: 3) По главным напряжениям в точке примыкания полки к стенке(т.А) в сечении, где одновременно возникают наиб. изгибающий момент и поперечная сила. Проверка в опасной т.Аосуществл. по одной из теорий прочности. Сначала в этой точке определ. главныенапряж. по ф-ле:
Подставляем главное напряжение в условие прочности по теории наиб.касат. напряжений: δ1 - δ3 Аналогично условие прочности по теории энергоформы изменения примет вид:
Деформации при изгибе. При действии нагрузок балка деформируется, а её ось искривляется. Изогнутую ось балки можно характеризовать двумя параметрами: 1) прогибом y; 2) углом поворота сечения θ. (Рисунок 1)
Прогибом балки в данном сечении наз. перемещение центра тяжести сечения в направлении перпендик. оси балки. Углом поворота сечения наз. угол поворота поперечного сечения к своему первоначальному положению. Изогнутая ось балки наз. упругой линией. Определение перемещений у и θ необходимы для расчёта элемента на жёсткость. Условие жёсткости требует что бы максимальный прогиб и угол поворота не превышали допускаемых значений 
Допускаемый прогиб устанавливается нормами проектирования в зависимости от назначения конструкции. Для балок это обычно Приближённое дифференциальное уравнение изогнутой оси балки. Рассмотрим балку нагруженную силой F.(рисунок 2)
Ранее была установлена зависимость Приравниваем правые части ур-ий (1) и(2)
Знаки кривизны и изгибающего момента совпадают если изогнутую ось поместить в 1-ом квадранте координатных осей т.е. начало координат выбирать в центре тяжести крайнего левого сечения балки, ось ординат направлять вверх, ось абсцисс совмещать с осью прямой балки :Mx>0, 1/p>0; Mx<0, 1/p<0.
Определение перемещений методом непосредственного интегрирования диф-ого уравнения. Для определения θ и y проинтегрируем диф-оеуравнене
C иD – постоянные интегрирования, определ. из граничных условий закрепления балки. Для консольной балки найти ymaxи θ max
Определим постоянные интегрированияC иD ПриZ=0 (защимление):y0=0, θ0=0
Найдём ymaxи θ max при z=l
Знак «-» угла поворота указывает что сечение повернулось по часовой стрелке, а знак «-» у прогиба означает что прогиб произошёл вниз. 4.Обобщенноеур-е изогнутой оси балки. Метод начальных параметров. 2) Изгибающий момент составляется от сил, расположенных левее исследуемого сечения. 3)При наличии сосредоточенного момента на балке изгибающий момент от него записывается в виде:
4) Если распред. Нагрузка не доходит до рассм. Сечения, то её необходимо продлить до сечения и приложить уравновешивающую нагрузку. 5) Интегрирование обобщенного ур-я производится без раскрытия скобок.
Рассм. Загруженную балку (рисунок!): Под действием нагрузок балка деформируется и в начале координат прогиб будет 1 уч. 2 уч.EI 5 уч. EI На смежных участках углы поворота и прогибы одинаковы. Из выражений углов поворота и прогибов следует: 5. Начальные параметры в обобщенном уравнении изогнутой оси балки, их определение. Если сразу известны нач. параметры Начальный угол поворота не равен нулю. Начальный прогиб = 0.
Если левый конец балки свободен, то оба нач. параметра не равны нулю.
Метод непосредственного интегрирования и метод начальных параметров применяется для балок постоянного поперечного сечения.
6. Энергетический метод определения перемещений.
Работа произвольнойсис-мы сил равна:
При применении энергетич. Метода как линейные, так и угловые перемещения обозначают Δ. Для определения работы внутренней силы, численно равной потенциальной энергии деформации, выделим из балки, находящейся в условиях чистого изгиба бесконечно малый элемент dz.
Это выражение даёт величину потенциальной энергии для элемента балки, находящегося в условиях чистого изгиба. При поперечном изгибе, когда кроме изгибающего момента, возникают и поперечные силы,ф-ла для вычисления энергии будет иметь вид: dU= Коэффициент К зависит от размеров сечения и в какой-то мере учитывает неравномерность распределения касат.напр-й по сечению. При вычислении энергии деф-ции изгиба поперечными силами Q можно пренебречь, т.к. последнее слагаемое составляет 2-3% от всей энергии деф-ции. Для вычисления энергии деф-ции балки в целом следует просуммировать значение dU по всей её длине. Окончательная ф-ла для определения энергии деф-ции при изгибе имеет вид:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 386. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





 R
R  3-я теория прочности или теор. наиб касат напряжений
3-я теория прочности или теор. наиб касат напряжений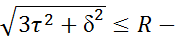 4-я теор. прочности
4-я теор. прочности – условие жёсткости.
– условие жёсткости. - длина пролёта.
- длина пролёта.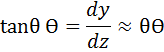
 – первая производная от прогиба равна углу поворота сечения
– первая производная от прогиба равна углу поворота сечения ; из высшей математики известно
; из высшей математики известно  , т.к.
, т.к.  – величина малая, ей можно пренебречь, получим
– величина малая, ей можно пренебречь, получим 

 - приближённое дифференциальное ур-е изогнутой оси балки.
- приближённое дифференциальное ур-е изогнутой оси балки. С учётом этого диф. ур-е в дальнейшем будет записываться со знаком +.
С учётом этого диф. ур-е в дальнейшем будет записываться со знаком +. ;
;  ;
;  ;
;

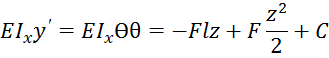










 .Запишем приближенное диф-ноеур-е для ряда участков.При записи ур-й использ. Правило знаков как для изгибающего момента.
.Запишем приближенное диф-ноеур-е для ряда участков.При записи ур-й использ. Правило знаков как для изгибающего момента. =0; EI
=0; EI  =
=  ; EIy=
; EIy= 
 z +
z + 
 =M(z-a)+
=M(z-a)+ 
 ;
; 
 . Для выяснения физической сущности постоянных интегрирования С и Dрассм. 1 уч.:
. Для выяснения физической сущности постоянных интегрирования С и Dрассм. 1 уч.: . Вывод:Постоянные интегрирования С и D представляют собой угол поворота и прогиб в начале координат,умноженные на жесткость балки.
. Вывод:Постоянные интегрирования С и D представляют собой угол поворота и прогиб в начале координат,умноженные на жесткость балки. ;E
;E  E
E  .В этих ур-х нач. параметры E
.В этих ур-х нач. параметры E  неизвестны. Их необходимо определить. Поэтому этот метод получил название-метод начальных параметров.
неизвестны. Их необходимо определить. Поэтому этот метод получил название-метод начальных параметров. можно сразу найти прогиб и угол попорота в любом сечении балки, но они не всегда известны. Нач. параметры опр-ся из граничных условий. Рассм. 1-ый и запишем:
можно сразу найти прогиб и угол попорота в любом сечении балки, но они не всегда известны. Нач. параметры опр-ся из граничных условий. Рассм. 1-ый и запишем: z=0;
z=0; 
 z=0;
z=0; 
 Находится из условия, что прогиб на 2-ой опоре = 0.
Находится из условия, что прогиб на 2-ой опоре = 0.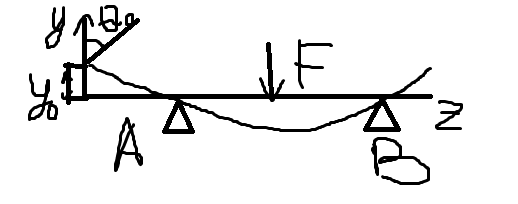 при z=0;
при z=0; 

 – теорема Клайперона
– теорема Клайперона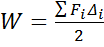


 ; dΘ=
; dΘ= 

