
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ОБЧИСЛЕННЯ ПОКАЗНИКОВОЇ ТА ЛОГАРИФМІЧНОЇ ФУНКЦІЙ ТАБЛИЧНО-АЛГОРІТМИЧНИМ МЕТОДОМ ⇐ ПредыдущаяСтр 8 из 8
6.1 Мета заняття: Вивчити на прикладах обчислень показникової та логарифмічної функцій можливості таблично-алгоритмічного методу.
Методичні вказівки Під час проектування спецпроцесорів обчислення показникової та логарифмічної функцій вводять як базові операції. Окрім цього, обчислення заданих функцій необхідне при використанні логарифмічної системи числення з метою скорочення часу виконання операцій множення, ділення та ін. Застосування таблично-алгоритмічного методу до показникової і логарифмічної функцій можливе з будь-якою основою “q”. Надалі розглядатимемо випадок q=2, як практично найбільш прийнятний.
6.2.1. Обчислення показникової функції. Нехай є показникова функція вигляду:
де х - дійсне число. З (6.1) виходить, що зміна аргументу на “k” одиниць (k – ціле число) призводить до зміни функції у 2k рази. Покажемо це. Введемо позначки:
де xін – значення аргументу на інтервалі задавання функції або інтервальне значення аргументу. Тоді
де yін – інтервальне значення функції. Таким чином, якщо зобразити функцію yін у табличній формі на деякому інтервалі з заданою відносною поxибкою, можливе обчислення функції y для області зміни аргументу, обмеженої тільки розрядною сіткою, з тією ж відносною поxибкою. При цьому з (6.3) слід, що для обчислення y виконується тільки операція зсуву.  Для показникової функції доцільно вибирати два інтервали табличного зображення функцій: Xпоч = 0, xкін = 1 для х ≥ 0, де yпоч = 1; yкін = 2 і xпоч = 0, xкін = -1 для х ≤ 0, де yпоч = 1; yкін= 0.5. Розрахунок табличних значень функції виконується таким чином. 1. Визначається відносна похибка обчислень функції dy, виходячи з аналізу задачі та структури спецпроцесора. На практичному занятті dy може бути задана викладачем. 2. Обчислюється перша похідна функції y′ у точках початкового yпоч і кінцевого значення yкін табличного інтервалу. Визначається найбільше по модулеві з цих двох значень похідної. Позначимо значення функції в точці з найбільшої похідної через 3. Визначається крок розбивки аргументу x у табличному інтервалі.
де 4. Визначається число розрядів nx двійкового коду аргументу в табличному інтервалі, відповідно до рівняння (5.4а) 5. Визначається число розрядів ny двійкового представлення функції відповідно до рівняння (5.5а) 6. Виконується обчислення табличних значень функціїyін з кроком Dх для табличних значень аргументу. На практичних заняттях, як таблиця, може бути використаний калькулятор. Процедура обчислення функції полягає ось в чому [7]. Виконується, якщо це необхідно, зведення аргументу x до інтервальних значень xін за допомогою співвідношення (6.2). За значенням аргументу xін з таблиці вибирається значення функціїyін, за яким відповідно до співвідношення (6.3) знаходиться значення функціїy. Остаточно сформулюємо правило обчислення показникової функції в двійковій системі числення. Якщо значення аргументу знаходиться в інтервалі табличного зображення функції, x Î [ xпоч, xкін ), значення функції визначається з таблиці. В тих випадках, коли x Ï [ xн, xк ), для дробової частини значення аргументу визначається відповідне до нього табличне значення функції, яке зсувається на “k” розрядів ліворуч, якщо x > 0 або на “k” розрядів праворуч, якщо x < 0.
Приклад проектування таблиці ПЗП для обчислювача показникової функції. Нехай y = 210,31 Обчислення виконаємо з відносною точністю: dy = 2-10 » 10-3 1. Маємо інтервал табличного зображення функції:
xпоч = 0; xкін = 1; yпоч = 1; yкін = 2.
2. Обчислимо похідну функції в точках: yпоч, yкін :
Таким чином, 3. Визначимо крок розбивки відповідно до (6.4)
4. Визначаємо число розрядів представлення аргументу – nx.
5. Визначаємо число розрядів представлення функції – ny.
6. Під час проектування спецпроцесора обчислюємо 210 інтервальниx значень функції з кроком Dx і точністю 10 розрядів. В нашому випадку при обчисленніyін скористуємось калькулятором, задаючи nx – розрядний аргумент і знімаючи ny – розрядний результат. Приклад процедури обчислення показникової функції. 1. Виділяємо з аргументу відповідно до (6.2) k и xін.
x = 10.31; k = 10; xін = 0.01001111012 » 0.3110
2. Знайдемо значення функції. По калькулятору yін = 1.00111101012 = 1.2392610. Тоді відповідно до (6.3) маємо
y = 210·1.00111101012 = 1001111010112 = 126910.
Точне значення по калькулятору – y = 1269.46. Відносна похибка обчислення: dy = 0.00039.
6.2.2 Обчислення логарифмічної функції. Нехай є логарифмічна функція вигляду:
y=log2x (6.5)
де х – додатне число. З (6.5.) виходить, що зміна аргументу в 2k рази (k – ціле додатне або від’ємне число), призводить до зміни цілої частини функції y на k одиниць. Справді, нехай аргумент зображений у формі:
де xm – мантиса, k – порядок. Після логарифмування цього виразу отримаємо:
Отже, якщо зобразити функцію в табличному вигляді на деякому інтервалі, на якому модуль значення функції менший за одиницю, то обчислення цього значення функції в усій області зміни аргументу можливе тільки за допомогою простиx операцій зсуву і вибірки з пам'яті. Для логарифмічної функції доцільно вибрати два інтервали табличного зображення функції.
xпоч = 1, xкін = 2 для y ≥ 0, де yпоч = 0, yкін = 1 xпоч = 0.5, xкін = 1 для y ≤ 0, де yпоч = -1, yкін = 0.
Тоді (6.6) приймає вигляд:
де
Розрахунок табличних значень функції виконується аналогічно тому, як це робиться для показникової функції. При цьому крок розбивки інтервалу визначаємо так:
де Обчислення виконаємо з відносною приведеною похибкою dy = 2–10. Наприклад, для інтервалу [1, 2) абсолютна похибка Dy приводиться до значення функції при x=2: y(2) = 1. Тоді
Dy = dy×y(2). (6.9)
Процедура обчислення функції в двійковій системі числення полягає ось в чому [7]. Нехай аргумент зображений двійковим nx – розрядним кодом. Можливі два випадки. В першому значення аргументу знаходиться в інтервалі табличного зображення функції, x Î[ xн, xк ). В цьому випадку значення функції визначається з таблиці. Другий випадок: x Ï[ xн, xк ). Виконується зсув аргументу на k розрядів праворуч, якщо x > 2 і на k розрядів ліворуч, якщо x < 0.5. Після цього значущі розряди аргументу потрапляють до інтервалу табличного зображення функції, що дозволяє отримати табличне значення функціїyін. Для отримання значення функції y до табличного значення функції слід приписати ліворуч від крапки число k з урахуванням знака, таким чином, що для x ³ 2, k - додатне, а для x ≤ 0.5, k – від’ємне. Приклад проектування таблиці ПЗП для обчислювача логарифмічної функції. Нехай Обчислення виконаємо з відносною приведеною похибкою dy = 2–10. Для інтервалу [1, 2) згідно (6.9): Dy = 1. Маємо інтервал табличного зображення функції:
Xпоч = 1; xкін = 2; yпоч = 0; yкін = 1.
2. Обчислимо похідну функції в точках: yпоч, yкін:
Таким чином, 3. Визначимо крок розбивки відповідно до (6.8)
4. Визначаємо число розрядів представлення аргументу - nx.
5. Визначаємо число розрядів представлення функції – ny.
6. Під час проектування спецпроцесора обчислюємо 211 інтервальниx значень функції з кроком Dx і точністю 10 розрядів. В нашому випадку при обчисленні yін скористаємося калькулятором, задаючи nx – розрядний аргумент і знімаючи ny – розрядний результат. Приклад процедури обчислення логарифмічної функції. 1. Визначаємо значення “k”:
x = 10011110110.012 , xін = 1.001111011002 » 1.240210.
Тобто для попадання в табличний інтервал необхідно виконати зсув аргументу на 10 розрядів вправо по відношенню до розрядної сітки. Таким чином, k = 10. 2. Знаходимо yін з таблиці (в нашому випадку по калькулятору)
yін = 0.0100111112 = 0.310610. Отже, відповідно до (6.7) маємо y = 10.3106.
Точне значення по калькулятору – y = 10.3109. Відносна похибка обчислення: dy = 0.0003.
Контрольні запитання та завдання
1. Яким способом визначають початкове й кінцеве значення аргументу для інтервалу при розрахунку показникової й логарифмічної функцій? 2. Наведіть основні співвідношення для приведення аргументу до інтервального значення при обчисленні показової й логарифмічної функцій. 3. Наведіть основні співвідношення для обчислення показової й логарифмічної функції по її інтервальному значенню. 4. Поясните основні етапи обчислення показникової і логарифмічної функцій таблично-алгоритмічним методом? ПЕРЕЛІК ПОСИЛАНЬ 1. Смирнов Ю.М., Воробьев Г.И. Специализированные ЭВМ. – М.: Высшая школа, 1989. 2. Байков В.Д., Смолов В.Б. Специализированные процессоры – М.: Радио и связь, 1985. 3. Самофалов К.Г., Луцкий Г.М. Основы теории многоуровневых конвейерных систем. – М.: Радио и связь, 1989. 4. Бадман О.Л., Миренков Н.Н. Специализированные процессоры для высокопроизводительной обработки данных. Новосибирск: Наука, 1988 5. Потапов В.И., Флоренсов А.Н. Таблично – алгоритмические вычисления функций в ЭВМ . – Иркутск:Издательство Иркутского университета, 1985. 6. Гусятин В.М. Таблично – алгоритмический метод вычисления степенной функции./ Вестник ХГПУ № 24. – Харьков: Изд. ХГПУ, 1999, С. 152 – 154. 7. Гусятин В.М., Янковский А.А. Быстрые алгоритмы вычисления логарифмической и показательной функций. – Харьковский технический университет радиоэлектроники. – Харьков. 1995 – 6 с. Деп. В ГНТБ Украины 23. 05. 95 № 1241 – УК 95. Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ до практичних занять з дисципліни “ПРОЕКТУВАННЯ СПЕЦПРОЦЕСОРІВ”
для студентів денної і заочної форми навчання спеціальності 7.091501 – Комп’ютерні системи та мережі
Упорядники: ГУСЯТІН Володимир Михайлович ЧАГОВЕЦЬ Ярослав Васильович БУГРІЙ Андрій Миколайович
Відповідальний випусковий О.Г. Руденко
Редактор
Комп’ютерна верстка
План 2007, поз. ___ Пiдп. до друку __.__.__. Формат 60´84 1/16. Спосіб друку – ризографія. Умов.друк.арк. 3,5 Облiк. вид.арк. ___ . Тираж 200 прим. Зам. № ______ Цiна договiрна.
ХНУРЕ. Україна. 61166, Харків, просп. Леніна, 14
Віддруковано в навчально-науковому видавничо-поліграфічному центрі ХНУРЕ 61166, Харків, просп. Леніна, 14 |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 467. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3) .
. (6.4)
(6.4)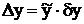
 , тоді
, тоді ;
;  .
. і, отже
і, отже  .
. .
.
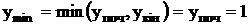 .
. ,
, .
.
 (6.6)
(6.6)

 (6.8)
(6.8) .25, δy=2-10.
.25, δy=2-10.
 , тоді
, тоді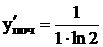 ;
; 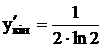 .
. і, отже
і, отже  .
. .
.
 .
.