
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СТРАТЕГІЯ ПОДВІЙНОГО КРОКУ ПРИ ОРГАНІЗАЦІЇ СИНХРОННОГО ІТЕРАЦІОНОГО ПРОЦЕСУ ОБЧИСЛЕННЯ ФУНКЦІЙ
3.1 Мета заняття: Вивчити двокрокову стратегію при організації синхронного ітераційного процесу на прикладі обчислення експоненціальної та логарифмічної функцій.
Методичні вказівки Експоненційна і логарифмічна функції мають гіршу збіжність порівняно з тригонометричними функціями. Тому при побудові ітераційного процесу використовується стратегія, за якої кожна константа в процесі обчислень застосовується двічі, тобто при виконанні двох кроків. Стратегія подвійного кроку Стратегію подвійного кроку розглянемо на прикладі функції
В наведених рівняннях індексом k задається номер кроку, kÎ{0, 1 … kмакс}. Як і в попередньому випадку, із зростанням kмакс зростає точність обчислень. Індекс i визначає значення константи і пов'язаний з індексом k рівнянням
де i Î {1, 2 …}; q = 2 визначають номери та число кроків, на яких індекс i не змінюється. Перед початком обчислень необхідно розрахувати значення константи ln(1 + xk·2-i) для xk Î {1, -1}. Виконаємо розрахунок константи до значень i = 7 та зведемо результати до таблиці 3.1.
Таблиця 3.1.
На першому етапі, під час обчислення ітераційного процесу для аргументу, величина jk наближається до нуля. Перед початком обчислень ітераційного процесу необхідно задати початкові умови, що в даному випадку дорівнюють: kпоч = 0; xпоч = 1; jпоч = φ; sign xпоч = sign φпоч. Приймемо jпоч = – 0.68. Тоді xпоч = –1; kмакс = 13.  Результати обчислень першого та другого етапів зведемо до таблиці 3.2.
Таблиця 3.2.
Розрахунковий результат виберемо за рядком k = 13, де отримане найкраще наближення jk+1 до нуля на першому етапі. Отже, маємо: результат розрахунковий х = 0.507, за калькулятором х = 0.5066, похибка Dx = |0.5066-0.507| = 0.0004.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 405. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
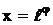 . Для обчислення функцій
. Для обчислення функцій 
 (3.1)
(3.1)
 , (3.2)
, (3.2)


