Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Додавання послідовних кодів старшими розрядами вперед у знакорозрядній системі численняДодавання двох чисел, починаючи зі старших розрядів, базується на екстраполяції значення переносу в отриману цифру суми за умови розповсюдження переносу не більш ніж на два розряди. Подібна екстраполяція можлива внаслідок надлишковості ЗРСЧ. Введемо позначення. Нехай потрібно обчислити суму C=A+B, де
Молодші значення індексу розрядної цифри відповідають старшим розрядам. Додавання здійснюється за тактами. Номер такту позначатимемо верхнім індексом k. В процесі обчислювання індекс k змінюється в межах k = 1, 2, … n, n+1, n+2. Причому k = i + 2, отже i = - 1, 0, 1, 2, … , n. Обчислення
де Початкові значення для рекурентного співвідношення (1.5) мають вигляд
Розглянемо приклад. Для перевірки правильності результату заздалегідь виконаємо паралельне додавання. Нехай
Зведемо додавання послідовних кодів до таблиці 1.3.
Таблиця 1.3
Результат додавання у табл. 1.3 співпадає з отриманим раніше результатом паралельного додавання. При знятті результатів обчислень положення крапки (коми) треба зсунути на два розряди в бік молодших розрядів. Контрольні запитання та завдання 1. Які особливості знакоразрядной системи числення Ви знаєте?  2. Поясните правило перекладу чисел з двійкової системи числення в знакорозрядну. 3. Поясните правило перекладу чисел із знакорозрядної в двійкову систему числення. 4. Викладете особливості виконання арифметичних операцій для паралельних операндів в знакорозрядной системі числення. 5. Викладете особливості підсумовування послідовних операндів в знакорозрядной системі числення.
ОБЧИСЛЕННЯ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ МЕТОДОМ ВОЛДЕРА 2.1 Мета заняття: Вивчити основні етапи обчислень тригонометричних функцій методом Волдера при синхронній організації ітераційного процесу [2].
Методичні вказівки Необхідно обчислити тригонометричні функції
Для початку виконання ітераційного процесу необхідно задати початкові умови, які в даному випадку дорівнюють iпоч = 0; yпоч = 0; xпоч = 1/Cт; jпоч = j; xпоч = 1; iÎ{0, 1, 2, 3, … , n-1} Тут Ст – коефіцієнт деформації, що треба обчислити для заданого числа n – кроків ітераційного процесу за таким співвідношенням:
Ст=
При збільшенні числа кроків n ітераційного процесу зменшується відносна наведена похибка обчислень - d . В нашому випадку (2.1) при використанні двійкової системи числення:
d ≤ 2-n (2.3) Перед початком обчислень слід знайти константи arctg2-i і звести їх до таблиці. Таблиця 2.1.
Значення констант для приклада, наведеного в таблиці 2.2, з урахуванням співвідношення (2.3) варто обчислювати з точністю до трьох значущих цифр після коми в градусах кутової величини. Повний цикл обчислень функцій Перший етап. На першому етапі організується ітераційній процес для аргументу j і на цьому етапі обчислюються коефіцієнти xi Î {±1}. При цьому в процесі обчислень значення ji наближатиметься до нуля:
Розглянемо приклад: j0 = 30о; x0 = 1, iпоч = 0; n = 10. При виконанні першого етапу доцільно зводити обчислення до таблиці 2.2:
Таблиця 2.2
Вибір значення функції на другому етапі здійснюється за номером рядка, в якому на першому етапі було отримано найкраще наближення, в нашому випадку, до нуля.
Другий етап. На другому етапі здійснюється обчислення функцій
Ст=1.647 при n=10.
Задамо початкові умови: xпоч = 1/Ст = 0.6073, yпоч = 0.
Таблиця 2.3.
Відповідно до результатів обчислень, що наведені у таблиці 2.2, слід результат обчислень у таблиці 2.3 вибирати по рядку i = 8, тому що на цьому рядку обчислень першого етапу було отримано найкраще наближення до нуля. Таким чином, маємо розрахункові значення
Для обчислення функції
Як вхідні дані виберемо значенняy = 0.5, x = 0.866, які обчислені за калькулятором для попереднього прикладу. Знайдемо кут j, відповідає вибраним значеннямy і x. Для побудови ітераційного процесу запишемо початкові умови iпоч = 0; yпоч = 0.5; xпоч = 0.866; jпоч = 0; xпоч = 1; n = 10. Перший етап. Всі обчислення зведемо до таблиці 2.4:
Таблиця 2.4
Другий етап. При обчисленні другого етапу скористаємось коефіцієнтами xi з таблиці 2.4. Результати обчислень зведемо до таблиці 2.5.
Таблиця 2.5
Відповідно до першого етапу результат слід вибирати на рядку i=8. Результат розрахунковий j = 30.0412, за вхідними данними j = 30. Абсолютна похибка обчислень: Dj = |30 – 30.0412| = 0.0412. Контрольні запитання та завдання
1. Навіщо в методі Волдера введений коефіцієнт деформації? 2. Чи можна при обчисленні тригонометричних функцій застосовувати асинхронний спосіб організації ітераційного процесу? 3. Які константи використовуються при обчисленні тригонометричних функцій? 4. Що таке початкові умови і поясните їх вибір на основі векторної моделі? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 459. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 виконується за правилом:
виконується за правилом: , (1.4)
, (1.4)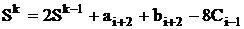 (1.5)
(1.5)




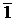




 ,
,  ,
,  . Для обчислень
. Для обчислень 
 (2.1)
(2.1)
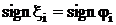
 (2.2)
(2.2) ,
, 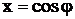 виконується в два етапи.
виконується в два етапи.



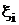


 ,
,  . Значення за калькулятором y = 0.5; x = 0.866. Абсолютна похибка обчислень:
. Значення за калькулятором y = 0.5; x = 0.866. Абсолютна похибка обчислень: ,
,  .
.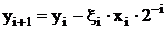
 (2.4)
(2.4)