
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модифікована стратегія подвійного кроку.Для зменшення обсягу обчислень синхронного ітераційного процесу стратегію подвійного кроку модифікують таким чином. Другий крок на першому етапі використовується тільки в тому випадку, якщо цей крок наближає до мети, тобто до заздалегідь відомого числа, наприклад, нуля або одиниці. В протилежному випадку, дані другого кроку не використовуються для подальшої побудови ітераційного процесу, а використовуються лише дані першого кроку. На другому етапі в такій ситуації другий крок минається. Модифіковану стратегію подвійного кроку розглянемо на прикладі логарифмічної функції. Логарифмічна функція, як і попередня експоненціальна, має гіршу збіжність порівняно з тригонометричними функціями. Тому в загальному випадку для обчислення логарифмічної функції за аналогією з експонентою, при побудові ітераційного процесу використовується стратегія подвійного кроку. Для обчислення функції
Обчислення індексу величини кроку ітерації – i виконується відповідно до рівняння (3.2). Початкові умови визначаються таким чином: xпоч = x; yпоч = 1-x; jпоч = 0; sign xпоч = sign yпоч. На першому етапі, в процесі обчислення ітераційного процесу для аргументу величина xk наближається до одиниці [2].
Таблиця 3.3.
 З таблиці 3.3. випливає, що на другому етапі з обчислень виключені два рядки k = 7, 11. При k = 13 маємо: результат розрахунковий j = –0.6808, за вхідними данними j = –0.68. Абсолютна похибка Dj = |–0.68 – (–0.6808)| = 0.0008.
Контрольні запитання та завдання
1. Поясните стратегію подвійного кроку і в яких випадках її використовують? 2. Які константи використовуються при обчисленні експоненціальної і логарифмічної функцій? 3. Поясните спосіб організації синхронного модифікованого процесу ітерацій. 4. Чи можливо при обчисленні експоненціальної і логарифмічної функцій застосувати асинхронний спосіб організації ітераційного процесу? 4 ВИКОНАННЯ МНОЖНО-ДІЛИЛЬНИХ ОПЕРАЦІЙ МЕТОДОМ ”ЦИФРА ЗА ЦИФРОЮ”
4.1 Мета заняття: Вивчити організацію обчислювального процесу методом “цифра за цифрою” під час виконання окремих операцій множення і ділення, а також складних множно-ділильниx операцій. Закріпити навички по організації синхронного, а також вивчити способи організації асинхронного ітераційного процесу на прикладі виконання множно-ділильниx операцій.
Методичні вказівки.
Метод “цифра за цифрою” є універсальним у тому розумінні, що з однаковим успіхом дозволяє обчислювати не тільки більшість функцій, але й виконувати арифметичні операції множення і ділення. При цьому вигляд ітераційних рівнянь зберігається, що дозволяє мати єдині для подібних задач апаратні засоби. Обчислення множно-ділильниx операцій можна виконати як синхронним, так і асинхронним методом організації ітераційного процесу. Ітераційні процеси при виконанні множно-ділильниx операцій мають добру збіжність і, отже, немає необхідності застосовувати стратегію подвійного кроку. Формально це можна записати як те, що k = i. Для обчислення множно-ділильниx операцій використовуються ітераційні рівняння [2].
Початкові умови мають вигляд: yпоч = А; Uпоч = 0; iпоч = 0; xпоч = 1. В даному ітераційному процесі обчисленняyi відповідає першому етапу, на якому y ® 0 зі збільшенням числа кроків. На другому етапі обчислюється функція U. Рівняння (4.1) дозволяють обчислювати комплексний множно-ділильний вираз типу:
U = (A/B) C (4.2)
Для спрощення рівнянь (4.1) припускається, що
úВú ³úАú , 0 £ С £ 1 (4.3)
У випадку, якщо вхідні дані у виразі (4.2) не задовольняють нерівностям (4.3), ці дані можуть бути зведені до певних нерівностей шляхом уведених масштабних множників пропорційних ступеню основи системи числення, в якій виконуються обчислення. Надалі такий масштаб дозволяє одержувати шукане число шляхом зсуву розрахункового результату по розрядній сітці на число розрядів, що дорівнює ступеню основи в масштабному множнику. Під час виконання окремих операцій множення або ділення в рівнянні (4.2) слід приймати відповідно B = 1 або С = 1. Виконаємо обчислення виразу (4.2), використовуючи синхронний і асинхронний методи організації ітераційного процесу. Нехай маємо А = 62,5; В = 0,75; С = 5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 432. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 використовуються ітераційні рівняння [2]:
використовуються ітераційні рівняння [2]:
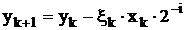 (4.1)
(4.1)






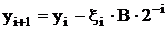
 (4.1)
(4.1)