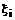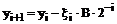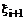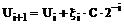Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Асинхронний спосіб організації ітераційного процесу.Розглянемо приклад обчислення операції ділення, використовуючи асинхронний спосіб організації ітераційного процесу. Для зменшення загального числа кроків при обчисленні ряду деяких функцій можливе застосування асинхронного методу побудови ітераційного процесу. До числа таких функцій відносяться експонента, логарифмічна функція та ін. [2]. На відміну від синхронного способу при побудові асинхронного ітераційного процесу можуть бути використані не всі константи. Більшість з них на другому етапі можна минути. На відміну від синхронного методу, в якому результат обчислень вибирається за рядком першого етапу, де маємо найкраще наближення аргументу до деякого відомого числа, в асинхронному методі результат вибирається за останнім рядком ітераційного процесу. Кількість кроків в такому випадку не задається. А ітераційний процес завершується по досягненню заданої похибки наближення – D на першому етапі. При асинхронному методі побудови ітераційного процесу можуть бути визначені різноманітні стратегії найкращого наближення аргументу на першому етапі до заздалегідь відомого значення. Розглянемо два методи організації асинхронного ітераційного процесу. Спосіб перший. В літературі [2] цей варіант асинхронної організації ітераційного процесу визначається як спосіб “спробного кроку”. В цьому випадку під час визначення коефіцієнтів напрямку руху Випадок перший, колиyпоч > 0, тоді приймають  Застосуємо спосіб “ спробного кроку”, тобто Вихідні дані А = 62.5; В = 0.75; С = 1, D = 0.001. Для зведення вxідниx даних до нерівностей (4.3) уведемо масштабні множники: А = 102·0.625, тобто MA = 102, B = 100·0.75, тобто MB = 100, C = 100·1, тобто MC = 100. Загальний масштаб дорівнює М = MA/MB·MC = 102. Визначимо початкові умови: yпоч = A = 0.625,
Таблиця 4.2.
З урахуванням масштабного множника МА = 102 маємо: Результат розрахунковий : U = 0.831·102 = 83.1, за калькулятором: U = 83.3. Абсолютна похибка DU = |83.3 – 83.1| = 0.2. Спосіб другий. В цьому випадку при визначенні коефіцієнтів напрямку руxу При незмінному початковому значенні yi по черзі для кожної константи розраховуються значення yi+1. Кожен результат, отриманий на i-му кроці, порівнюється з результатом, отриманим на i+1-му кроці. Якщо çyi+1ç<çyiç, то ітерація триває й на другому етапі на цих кроках функція не обчислюється. У випадку якщо çyi+1ç>çyiç, те i-й крок у цьому випадку є найкращим і на цьому кроці на другому етапі обчислюється функція. При наступних ітераціях за початкове значення yi вибирається значення найкращого попереднього кроку. При цьому значення yi+1 необхідно перерахувати при початковому значенні найкращого кроку. Обчислення на першому етапі завершуються, коли виконується співвідношення yi ≤ D. Природно, що при такій стратегії руху буде потрібно найменше число кроків для одержання необхідної точності обчислення функції. Надалі цей спосіб визначимо, як спосіб ú Diú мін. Розглянемо даний метод на прикладі обчислення операцій множення. Вихідні дані: А = 36.8, В = 1, С = 1.68, D = 0.001. Для приведення вихідних даних до нерівностей (4.3) введемо масштабні множники: А = 102·0.368; С = 101·0.168, тобто MA = 102, MC = 101. Загальний масштаб дорівнює М = MA·MC = 103. Визначимо початкові умови: yпоч = A = 0.368, Результати обчислень зведемо до таблиці 4.3. Таблиця 4.3.
Сірим кольором в таблиці позначені строки, в яких значення yi+1 були перераховані при значенні yi найкращого кроку. Враховуючи масштабний множник М = МА·МС = 103 маємо: результат розрахунковий U = 0.06170·103 = 61.7, результат за калькулятором U = 61.824. Абсолютна похибка DU = |61.824 – 61.7| = 0.124. Контрольні запитання та завдання 1. Навіщо використовується масштабування вхідних величин при обчисленні множно-ділильних операцій ітераційним методом? 2. Поясните асинхронний спосіб організації ітераційного процесу методом «пробного кроку» при обчисленні операції ділення. 3. Поясните асинхронний спосіб організації ітераційного процесу методом «спробного кроку» при обчисленні операції множення. 4. Як задаються початкові умови при обчисленні множо-ділильних операцій і окремо операцій множення і ділення? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 376. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
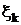 на першому етапі можливі два випадки.
на першому етапі можливі два випадки.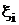 Î{0,1}. Причому, якщо в процесі виконання ітерацій yi > 0, то
Î{0,1}. Причому, якщо в процесі виконання ітерацій yi > 0, то 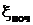 = 1,
= 1,