
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения Лагранжа 2–го родаОбщее уравнение динамики (7.7) даёт возможность составлять дифференциальные уравнения движения, не содержащие реакций идеальных связей. Для сравнительно простых механических систем непосредственное применение этого уравнения вполне оправдано, однако, в более сложных случаях использование общего уравнения динамики приводит, как правило, к относительно сложным преобразованиям. Поэтому значительно удобнее пользоваться не общим уравнением динамики, а вытекающими из него уравнениями Лагранжа 2–го рода, в которых для голономных систем основные трудности преобразований преодолеваются уже в общем виде. Уравнения Лагранжа 2-го рода имеют вид: где
Каток
Система имеет две степени свободы. В качестве обобщенных координат примем координату 
Уравнения Лагранжа 2–го рода в рассматриваемом случае имеют вид:
Кинетическая энергия в рассматриваемом случае не зависит явным образом от обобщенных координат, поэтому
Вычислим частные производные по обобщенным скоростям:
Для вычисления обобщенных сил используем формулы (7.23): пусть
пусть
где Положим для определенности
Интегрируя полученную систему уравнений при нулевых начальных условиях, находим:
где
причём,
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1 ПЕРВАЯ И ВТОРАЯ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ Пример 1.1
Груз
Рассмотрим движение груза
Последнее уравнение позволяет определить силу
Заметим, что в решении фигурирует сила реакции нити, но искомая сила натяжения нити равна ей по модулю.
Пример 1.2
Автомобиль массы
Рассмотрим автомобиль в верней точке моста. Силы, действующие в направлении касательной к траектории – сила трения, сила сопротивления воздуха неизвестны. В направлении главной нормали к траектории действуют известная сила тяжести и нормальная реакция опоры, которую и требуется определить. Поэтому запишем уравнение движения в проекциях на главную нормаль к траектории. В рассматриваемом случае это уравнение принимает вид:
По третьему закону Ньютона сила давления автомобиля на мост по модулю равна нормальной реакции.
Пример 1.3 Решето рудообогатительного грохота движется поступательно по вертикали по закону
Направим ось
Отсюда:
Минимальное значение нормальная реакция принимает в верхней точке, где
Если кусок руды отделяется от решета, то
Пример 1.4
Материальная точка массы
Направим ось
Интегрируя полученное дифференциальное уравнение движения точки
определяем зависимость ее скорости от времени: Поскольку
интегрируя которое, определяем закон движения точки:
Пример 1.5 На какую высоту
или, учитывая что
Уравнение
отсюда:
Теперь мы имеем возможность определить время подъема тела на максимальную высоту. Подставляя в уравнение (с) условия при Остается определить максимальную высоту подъема
представляется неудобным. Помимо зависимости
Уравнение Интегрируя уравнение
Заметим, что соотношение
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 752. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 – кинетическая энергия системы;
– кинетическая энергия системы;  – обобщенная координата;
– обобщенная координата;  – обобщенная скорость;
– обобщенная скорость;  – обобщенная сила;
– обобщенная сила;  – число степеней свободы системы.
– число степеней свободы системы. , представляющий собой сплошной однородный цилиндр массы
, представляющий собой сплошной однородный цилиндр массы  радиуса
радиуса  , катится без проскальзывания по горизонтальной поверхности. К оси катка привязан трос, переброшенный через неподвижный блок
, катится без проскальзывания по горизонтальной поверхности. К оси катка привязан трос, переброшенный через неподвижный блок  и растягиваемый грузом
и растягиваемый грузом 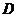 , масса которого
, масса которого  (Рис.7.11). Блок
(Рис.7.11). Блок  . В начальный момент система находится в покое, пружина не растянута. Определить движение системы, предполагая, что при качении катка возникает постоянный момент сопротивления
. В начальный момент система находится в покое, пружина не растянута. Определить движение системы, предполагая, что при качении катка возникает постоянный момент сопротивления  .
.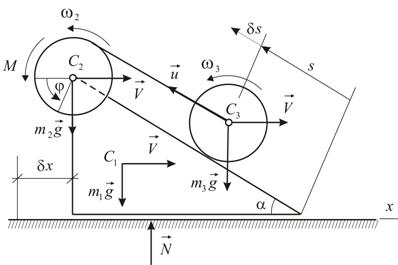
 оси катка и удлинение пружины
оси катка и удлинение пружины  . Вычислим кинетическую энергию системы:
. Вычислим кинетическую энергию системы:
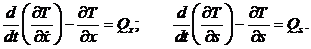
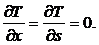

 тогда
тогда
 тогда
тогда
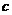 — коэффициент жесткости пружины.
— коэффициент жесткости пружины. В этом случае уравнения Лагранжа примут вид:
В этом случае уравнения Лагранжа примут вид:
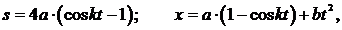


 массы
массы  , подвешенный на нити длины
, подвешенный на нити длины  , другой конец которой закреплен в точке
, другой конец которой закреплен в точке  , представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости (Рис.1.1). Нить образует с вертикалью угол
, представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости (Рис.1.1). Нить образует с вертикалью угол 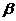 . Определить скорость груза
. Определить скорость груза 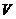 и силу натяжения нити
и силу натяжения нити 

 Из первого уравнения можно сделать вывод, что в процессе движения скорость точки не изменяет свою величину; определить эту величину можно из второго уравнения:
Из первого уравнения можно сделать вывод, что в процессе движения скорость точки не изменяет свою величину; определить эту величину можно из второго уравнения:
 . Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
. Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
 отсюда:
отсюда: 
 . Найти наименьшую частоту
. Найти наименьшую частоту  колебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.
колебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.


 :
:
 отсюда
отсюда
 , где
, где 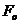 и
и  — постоянные величины. В начальный момент точка имела скорость
— постоянные величины. В начальный момент точка имела скорость  . Найти уравнение движения точки.
. Найти уравнение движения точки.


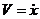 , полученное уравнение представляет собой дифференциальное уравнение относительно функции
, полученное уравнение представляет собой дифференциальное уравнение относительно функции  :
:

 и за какое время
и за какое время  , брошенное вертикально вверх со скоростью
, брошенное вертикально вверх со скоростью  , где
, где  на поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:
на поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:
 , вид:
, вид: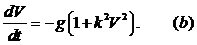
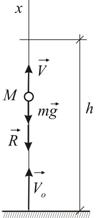
 представляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:
представляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:
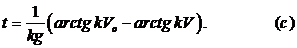
 получаем
получаем 
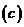 можно рассматривать как дифференциальное уравнение относительно функции
можно рассматривать как дифференциальное уравнение относительно функции 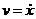 , но интегрирование уравнения
, но интегрирование уравнения
 , поскольку скорость в верхней точке известна:
, поскольку скорость в верхней точке известна: 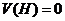 . Перейдем в уравнении
. Перейдем в уравнении  от производной по
от производной по  к производной по
к производной по 


 получаем:
получаем: 