
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Возможные скорости и возможные перемещенияПонятия возможной скорости и возможного перемещения введем сначала для материальной точки, на которую наложена голономная удерживающая нестационарная связь. Возможной скоростью материальной точки
Заметим, что возможная скорость не реализуется как следствие действия приложенных к точке сил. Это – мыслимый набор скоростей, обладая которыми в данном положении
Возможным перемещением материальной точки
Действительное перемещение и действительная скорость связаны известным соотношением
Идеальные связи
Связи, наложенные на механическую систему, называются идеальными, если сумма работ всех реакций связей на любом возможном перемещении системы равна нулю: Учитывая важность понятия идеальной связи, рассмотрим часто встречающиеся случаи. 1.Пусть опорой для тела служит некоторая поверхность, по которой тело может скользить (Рис. 7.4). В общем случае реакция поверхности 
Если же поверхность идеальная, то сила трения отсутствует и Особый случай составляет качение без проскальзывания колеса по поверхности. Сила реакции снова имеет две составляющие
2. Рассмотрим две материальные точки Для возможной суммарной мощности сил реакций получаем:
Если стержень 3. Неподвижный шарнир может рассматриваться как идеальная связь, если трением в шарнире можно пренебречь (Рис. 7.7). В этом случае. поскольку точка приложения реакции шарнира неподвижна. возможная работа реакции шарнира равна нулю. Если же трение в шарнире необходимо учитывать, то связь не будет идеальной, так как при возможном повороте тела вокруг шарнира будет совершать работу момент сил трения.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ЛЕКЦИЯ 7 (15)
7.4. Принцип возможных перемещений Принцип возможных перемещений устанавливает условия равновесия механических систем. Под равновесием механической системы традиционно понимают состояние ее покоя по отношению к выбранной инерциальной системе отсчета. Рассмотрим механическую систему, состоящую из
где
Для равновесия механической системы с идеальными удерживающими стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к системе активных сил на любом возможном перемещении системы равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю:
Сформулированное утверждение называют принципом возможных перемещений. Необходимость. Пусть механическая система находится в равновесии. Следовательно, выполняются условия (7.1). Из данного положения дадим системе возможное перемещение. Умножим каждое из уравнений (7.1) скалярно на соответствующее точке возможное перемещение
По условию связи идеальные, следовательно, справедливо равенство (6.7). Из (6.7) и (7.3) получаем (7.2). Достаточность. Приложим к точкам покоящейся механической системы систему сил, удовлетворяющих равенству (7.2) и, следовательно, поскольку связи идеальные (6.7), равенству Покажем, что механическая система останется в покое. Допустим противное – система под действием приложенных сил пришла в движение, т.е. ее точки получили ускорения Это равенство может иметь место только в том случае, если ускорения всех точек равны нулю Заметим, что если вместо возможных перемещений использовать пропорциональные им возможные скорости (что позволяет в полной мере использовать при решении задач кинематические методы), то условия равновесия записываются в виде:
т.е. для равновесия механической системы с идеальными, удерживающими, стационарными связями необходимо и достаточно, чтобы сумма мощностей всех приложенных к системе активных сил при любых возможных скоростях ее точек равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю.
Пример 1 Определить зависимость между модулями сил
Дадим системе возможное перемещение: пусть
При исследовании условий равновесия механизмов в зависимости от конкретной задачи, исходя из соображений удобства, можно использовать как возможные скорости, так и возможные перемещения. Для сравнения в этом первом разбираемом примере рассмотрим и возможные перемещения, и возможные скорости. Условия равновесия системы можно записать в виде (7.2): Возможные перемещения связаны между собой соотношениями Теперь условия равновесия записываются в виде: Отсюда:
Пример 2 Полиспаст состоит из неподвижного блока и
Условие равновесия (7.5) имеет вид Рассмотрим первый из подвижных блоков. Точка Подставляя полученный результат в условие равновесия, имеем:
Общее уравнение динамики
Рассмотрим механическую систему, состоящую из
где
При фиксированном времени дадим точкам системы возможные перемещения. Умножим каждое из уравнений движения скалярно на соответствующее возможное перемещение и сложим все полученные уравнения:
Поскольку по условию связи идеальные (6.7), последняя сумма равна нулю и, следовательно,
Уравнение (7.6) называется общим уравнением динамики. При использовании общего уравнения динамики удобно вводить в рассмотрение силы инерции. В этом случае уравнение (7.6) принимает вид:
Равенство (7.7) составляет содержание так называемого принципа Лагранжа–Даламбера:
в каждый момент времени для механической системы с идеальными удерживающими связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении системы равна нулю.
Пример Призма массы
Силовая и кинематическая схемы представлены на Рис.7.10. Общее уравнение динамики в рассматриваемом случае имеет вид:
Система имеет две степени свободы. В качестве независимых координат примем координату призмы Отсюда: Учитывая, что
получаем общее уравнение динамики в виде:
Поскольку возможные перемещения
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ЛЕКЦИЯ 8 (16)
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 835. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется любая скорость, которую может иметь несвободная материальная точка, не нарушая наложенных на нее в данный момент времени связей.
называется любая скорость, которую может иметь несвободная материальная точка, не нарушая наложенных на нее в данный момент времени связей. , точка не покинет поверхность связи (напомним, рассматриваются только удерживающие связи) при условии, что сама поверхность не движется и не деформируется, т.е. при фиксированном времени.
, точка не покинет поверхность связи (напомним, рассматриваются только удерживающие связи) при условии, что сама поверхность не движется и не деформируется, т.е. при фиксированном времени. называется любое бесконечно малое перемещение, которое может иметь несвободная материальная точка, не нарушая наложенных на нее в данный момент времени связей.
называется любое бесконечно малое перемещение, которое может иметь несвободная материальная точка, не нарушая наложенных на нее в данный момент времени связей.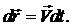
 (7.1)
(7.1)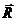 имеет две составляющие – нормальную
имеет две составляющие – нормальную  и касательную
и касательную  , которая называется силой трения. При любом возможном перемещении тела возможная работа реакции отлична от нуля за счет работы силы трения:
, которая называется силой трения. При любом возможном перемещении тела возможная работа реакции отлична от нуля за счет работы силы трения:

 (Рис. 7.5). При любом возможном перемещении колеса скорость точки приложения сил
(Рис. 7.5). При любом возможном перемещении колеса скорость точки приложения сил  , то такая связь будет идеальной.
, то такая связь будет идеальной.

 и
и  , связанные невесомым деформируемым стержнем (Рис. 7.6). В соответствии с третьим законом Ньютона
, связанные невесомым деформируемым стержнем (Рис. 7.6). В соответствии с третьим законом Ньютона  . По теореме сложения скоростей при сложном движении точки
. По теореме сложения скоростей при сложном движении точки  где
где  и
и  – составляющие возможной относительной скорости, направленные вдоль отрезка
– составляющие возможной относительной скорости, направленные вдоль отрезка  и перпендикулярно ему соответственно.
и перпендикулярно ему соответственно.



 то суммарная возможная работа реакций равна нулю и связь будет идеальной. Такая связь реализуется в абсолютно твердом теле. Если же возможна деформация стержня, рассмотренная связь не будет идеальной, поскольку возможная работа реакций при растяжении–сжатии стержня будет отлична от нуля.
то суммарная возможная работа реакций равна нулю и связь будет идеальной. Такая связь реализуется в абсолютно твердом теле. Если же возможна деформация стержня, рассмотренная связь не будет идеальной, поскольку возможная работа реакций при растяжении–сжатии стержня будет отлична от нуля. материальных точек. Для ее равновесия необходимо и достаточно, чтобы суммы всех сил, действующих на каждую точку системы, и скорости всех точек в начальный момент времени равнялись нулю:
материальных точек. Для ее равновесия необходимо и достаточно, чтобы суммы всех сил, действующих на каждую точку системы, и скорости всех точек в начальный момент времени равнялись нулю: (7.1)
(7.1) – равнодействующая всех активных сил, действующих на точку с номером
– равнодействующая всех активных сил, действующих на точку с номером  ;
; – равнодействующая всех сил реакций связей, наложенных на точку с номером
– равнодействующая всех сил реакций связей, наложенных на точку с номером  (7.2)
(7.2) и сложим все полученные уравнения:
и сложим все полученные уравнения: (7.3)
(7.3) (7.4)
(7.4) . Эти ускорения должны быть направлены по касательным к траекториям точек, поскольку скорости равны нулю и нормальные составляющие ускорений отсутствуют. Таким образом, действительные перемещения точек пропорциональны их ускорениям. По условию связи стационарные и, следовательно, среди возможных перемещений системы найдется такое, которое совпадает с действительным. Возьмем в качестве возможного перемещения систему векторов, пропорциональных ускорениям точек
. Эти ускорения должны быть направлены по касательным к траекториям точек, поскольку скорости равны нулю и нормальные составляющие ускорений отсутствуют. Таким образом, действительные перемещения точек пропорциональны их ускорениям. По условию связи стационарные и, следовательно, среди возможных перемещений системы найдется такое, которое совпадает с действительным. Возьмем в качестве возможного перемещения систему векторов, пропорциональных ускорениям точек  . Равенство (7.4) примет вид:
. Равенство (7.4) примет вид:  или, учитывая, что для каждой точки справедлив второй закон Ньютона,
или, учитывая, что для каждой точки справедлив второй закон Ньютона, 
 Следовательно, механическая система после приложения активных сил останется в покое.
Следовательно, механическая система после приложения активных сил останется в покое. (7.5)
(7.5) и
и  в клиновом прессе, если сила приложена к концу рукоятки длины
в клиновом прессе, если сила приложена к концу рукоятки длины  перпендикулярно плоскости, содержащей рукоятку и ось винта (Рис.7.8). Шаг винта равен
перпендикулярно плоскости, содержащей рукоятку и ось винта (Рис.7.8). Шаг винта равен  . Угол при вершине клина
. Угол при вершине клина  .
. – угол поворота рукоятки;
– угол поворота рукоятки; 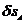 – перемещение точки
– перемещение точки  – горизонтальное перемещение клина;
– горизонтальное перемещение клина;  – вертикальное перемещение точки
– вертикальное перемещение точки 

 . Отсюда:
. Отсюда: 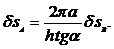
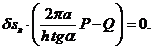

 поднимаемого груза
поднимаемого груза  , приложенной к свободному концу
, приложенной к свободному концу 
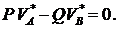
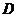 – мгновенный центр скоростей блока. Возможная скорость точки
– мгновенный центр скоростей блока. Возможная скорость точки  численно равна возможной скорости точки
численно равна возможной скорости точки  Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом,
Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом, 



 (7.6)
(7.6) (7.7)
(7.7) может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки. Конец троса прикреплен к оси катка, который катится без скольжения по боковой поверхности призмы. Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы
может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки. Конец троса прикреплен к оси катка, который катится без скольжения по боковой поверхности призмы. Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы  и одинакового радиуса
и одинакового радиуса  . К барабану лебедки приложен постоянный вращающий момент
. К барабану лебедки приложен постоянный вращающий момент  . Составить дифференциальные уравнения движения системы.
. Составить дифференциальные уравнения движения системы.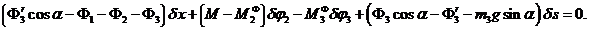

 и относительную координату оси катка
и относительную координату оси катка  . Кинематические условия, налагаемые связями, имеют вид:
. Кинематические условия, налагаемые связями, имеют вид: 
 и
и 





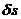 могут принимать любые значения и не зависят друг от друга, общее уравнение динамики распадается на систему двух дифференциальных уравнений относительно координат
могут принимать любые значения и не зависят друг от друга, общее уравнение динамики распадается на систему двух дифференциальных уравнений относительно координат 
